Thursday, December 25, 2025
Multivariable Function Limits: UNIZOR.COM - Math4Teens - Calculus - Limi...
Notes to a video lecture on http://www.unizor.com
Multivariable Limits
Sometimes we have to deal with functions of two or more arguments and have to analyze the behavior of such functions as their arguments approach certain values.
The usual way to analyze this situation is to fix all arguments except one and see what happens with the function if that single argument approach the value we are interested in.
The result of this process is the reduction of variables by one, and we can repeat the same thing for the next argument, then the next etc.
For example, consider a function
F(x,y,z) =
= arctan(x) + 2−y + z/(z+1)
and its behavior when all arguments increase without restriction.
1. Fix x and y, let z→+∞.
limz→+∞ z/(z+1) = 1
2. Our function now can be written as
F(x,y,+∞) = arctan(x)+2 −y+1
Fix x, let y→+∞.
limy→+∞ 2−y = 0
3. Our function now is
F(x,+∞,+∞) = arctan(x)+0+1
Let x→+∞.
limx→+∞ arctan(x) = π/2
The limit of our function when z→+∞, y→+∞, x→+∞ is
lim F(x,y,z) = π/2 + 1
This is great, but we have a result that seems to depend on the order of arguments we analyze.
Can the result be different if we choose a different order, say, fix z and y getting a limit by x, then fix z getting a limit by y and finish with a limit by z?
The answer is:
Under certain relatively broad conditions, the final result is not dependent on the order of taking limits by different arguments.
We consider only a case of a function of two arguments (in a general case of many arguments the proof is similar but a bit more tedious) and prove the theorem below.
Prior to that, let's talk about a particular type of taking a multivariable function to a limit - a uniform convergence.
Assume, we have to analyze the limit of function F(x,y) as x→a and y→b.
We say that function F(x,y) is converging uniformly by y to Y(y) as x→a if for any positive ε there is positive δ such that
|F(x,y)−Y(y)| < ε
as long as both |x−a| < δ and |y−b| < δ.
In other words, as x→a, not only F(x,y)→Y(y) for any specific value of y (so-called point convergence of F(x,y) to Y(y)), but F(x,y) gets equally close to Y(y) (distance less than small ε) for all values of y within certain neighborhood of its limit point y=b.
Theorem
Assume that all limits below exists and satisfy the conditions listed.
IF
limy→b F(x,y) = X(x)
uniformly by x
limx→a X(x) = A
limx→a F(x,y) = Y(y)
uniformly by y
limy→b Y(y) = B
THEN
A = B
Proof
Assume, A ≠ B.
Let |A−B|=d.
Let ε=d/4.
Then the following logic holds.
limx→a F(x,y) = Y(y) (uniformly by y) ⇒
⇒ ∃δa: |Y(y)−F(x,y)| < ε ∀x∈[a−δa,a+δa] and
∀y∈[b−δa,b+δa]
limy→b Y(y) = B ⇒
⇒ ∃δb: |B−Y(y)| < ε
∀y∈[b−δb,b+δb]
Let δ = min(δa,δb)
Then from both above statements follows that within a small neighborhood of limit points x=a and y=b
∀x∈[a−δ,a+δ] and
∀y∈[b−δ,b+δ]
the following is true
|B−Y(y)|<ε and
|Y(y)−F(x,y)|<ε
from which, in turn, follows
|B−F(x,y)|<2ε=d/2
That is, within a small distance of arguments x and y around their limit points a and b the value of F(x,y) deviates from B by less than d/2.
Now repeat the same from the position of another limit of function F(x,y).
limy→b F(x,y) = X(x) (uniformly by x) ⇒
⇒ ∃γb: |X(x)−F(x,y)| < ε ∀x∈[a−γb,a+γb] and
∀y∈[b−γb,b+γb]
limx→a X(x) = A ⇒
⇒ ∃γa: |A−X(x)| < ε
∀x∈[a−γa,a+γa]
Let γ = min(γa,γb)
Then from both above statements follows that within a small neighborhood of limit points x=a and y=b
∀x∈[a−γ,a+γ] and
∀y∈[b−γ,b+γ]
the following is true
|A−X(x)|<ε and
|X(x)−F(x,y)|<ε
from which, in turn, follows
|A−F(x,y)|<2ε=d/2
That is, within a small distance of arguments x and y around their limit points a and b the value of F(x,y) deviates from A by less than d/2.
Make our neighborhood even smaller by choosing β=min(γ,δ) and consider
∀x∈[a−β,a+β] and
∀y∈[b−β,b+β]
Now we see that within this neighborhood F(x,y) is closer to A by less than d/2 and closer to B by less than d/2, where d is the distance between A and B, which is impossible.
Therefore, A = B.
Multivariable Limits
Sometimes we have to deal with functions of two or more arguments and have to analyze the behavior of such functions as their arguments approach certain values.
The usual way to analyze this situation is to fix all arguments except one and see what happens with the function if that single argument approach the value we are interested in.
The result of this process is the reduction of variables by one, and we can repeat the same thing for the next argument, then the next etc.
For example, consider a function
F(x,y,z) =
= arctan(x) + 2−y + z/(z+1)
and its behavior when all arguments increase without restriction.
1. Fix x and y, let z→+∞.
limz→+∞ z/(z+1) = 1
2. Our function now can be written as
F(x,y,+∞) = arctan(x)+2 −y+1
Fix x, let y→+∞.
limy→+∞ 2−y = 0
3. Our function now is
F(x,+∞,+∞) = arctan(x)+0+1
Let x→+∞.
limx→+∞ arctan(x) = π/2
The limit of our function when z→+∞, y→+∞, x→+∞ is
lim F(x,y,z) = π/2 + 1
This is great, but we have a result that seems to depend on the order of arguments we analyze.
Can the result be different if we choose a different order, say, fix z and y getting a limit by x, then fix z getting a limit by y and finish with a limit by z?
The answer is:
Under certain relatively broad conditions, the final result is not dependent on the order of taking limits by different arguments.
We consider only a case of a function of two arguments (in a general case of many arguments the proof is similar but a bit more tedious) and prove the theorem below.
Prior to that, let's talk about a particular type of taking a multivariable function to a limit - a uniform convergence.
Assume, we have to analyze the limit of function F(x,y) as x→a and y→b.
We say that function F(x,y) is converging uniformly by y to Y(y) as x→a if for any positive ε there is positive δ such that
|F(x,y)−Y(y)| < ε
as long as both |x−a| < δ and |y−b| < δ.
In other words, as x→a, not only F(x,y)→Y(y) for any specific value of y (so-called point convergence of F(x,y) to Y(y)), but F(x,y) gets equally close to Y(y) (distance less than small ε) for all values of y within certain neighborhood of its limit point y=b.
Theorem
Assume that all limits below exists and satisfy the conditions listed.
IF
limy→b F(x,y) = X(x)
uniformly by x
limx→a X(x) = A
limx→a F(x,y) = Y(y)
uniformly by y
limy→b Y(y) = B
THEN
A = B
Proof
Assume, A ≠ B.
Let |A−B|=d.
Let ε=d/4.
Then the following logic holds.
limx→a F(x,y) = Y(y) (uniformly by y) ⇒
⇒ ∃δa: |Y(y)−F(x,y)| < ε ∀x∈[a−δa,a+δa] and
∀y∈[b−δa,b+δa]
limy→b Y(y) = B ⇒
⇒ ∃δb: |B−Y(y)| < ε
∀y∈[b−δb,b+δb]
Let δ = min(δa,δb)
Then from both above statements follows that within a small neighborhood of limit points x=a and y=b
∀x∈[a−δ,a+δ] and
∀y∈[b−δ,b+δ]
the following is true
|B−Y(y)|<ε and
|Y(y)−F(x,y)|<ε
from which, in turn, follows
|B−F(x,y)|<2ε=d/2
That is, within a small distance of arguments x and y around their limit points a and b the value of F(x,y) deviates from B by less than d/2.
Now repeat the same from the position of another limit of function F(x,y).
limy→b F(x,y) = X(x) (uniformly by x) ⇒
⇒ ∃γb: |X(x)−F(x,y)| < ε ∀x∈[a−γb,a+γb] and
∀y∈[b−γb,b+γb]
limx→a X(x) = A ⇒
⇒ ∃γa: |A−X(x)| < ε
∀x∈[a−γa,a+γa]
Let γ = min(γa,γb)
Then from both above statements follows that within a small neighborhood of limit points x=a and y=b
∀x∈[a−γ,a+γ] and
∀y∈[b−γ,b+γ]
the following is true
|A−X(x)|<ε and
|X(x)−F(x,y)|<ε
from which, in turn, follows
|A−F(x,y)|<2ε=d/2
That is, within a small distance of arguments x and y around their limit points a and b the value of F(x,y) deviates from A by less than d/2.
Make our neighborhood even smaller by choosing β=min(γ,δ) and consider
∀x∈[a−β,a+β] and
∀y∈[b−β,b+β]
Now we see that within this neighborhood F(x,y) is closer to A by less than d/2 and closer to B by less than d/2, where d is the distance between A and B, which is impossible.
Therefore, A = B.
Thursday, December 18, 2025
Double Sequence Limits: UNIZOR.COM - Math4Teens - Calculus - Limit of Se...
Notes to a video lecture on http://www.unizor.com
Double Limits
Sometimes we are interested in sequences that depend on two natural numbers like {am,n}.
For example,
am,n=arctan(m)+2−n.
Now, if m→∞ and n→∞, how to calculate the limit of am,n?
It might be
limm→∞ [limn→∞ (am,n)]
or
limn→∞ [limm→∞ (am,n)]
depending on which index, m or n, we will use to go to a limit first, and there is no guarantee that the answers will be the same.
Let's check both methods.
limn→∞ (am,n) =
= limn→∞ (arctan(m) + 2−n) =
= arctan(m)
limm→∞ (arctan(m)) = π/2
If we change the order of limits,
limm→∞ (am,n) =
= limm→∞ (arctan(m) + 2−n) =
= π/2 + 2−n
limn→∞ (π/2 + 2−n) = π/2
As you see, the results are the same.
In some way, the equality of these two limits might be considered similar to a standard accounting procedure of checking the calculations.
Imagine an M⨯N matrix with numbers.
If you summarize the numbers within each of M rows with row #i having a sum Ri and summarize all these row totals by i from 1 to M, you will get a total of all numbers in an original table.
If you summarize the numbers within each of N columns with column #j having a sum Sj and summarize all these column totals by j from 1 to N, you should get exactly the same total of all numbers.
If these two calculated totals are not equal, that is if
Σi∈[1,M] Ri ≠ Σj∈[1,N] Sj
then your calculations are wrong.
The equality of two limits in the example above is not coincidental. We shall prove it as the theorem below.
But, to make our proof rigorous, we have to make a short comment about uniform convergence.
We say that sequence {am,n} is converging uniformly by m to bm as n→∞ if for any positive ε there is number K such that
|bm−am,n| < ε
as long as both n and m are greater than K.
Analogously, we say that sequence {am,n} is converging uniformly by n to cn as m→∞ if for any positive ε there is number K such that
|cn−am,n| < ε
as long as both n and m are greater than K.
Theorem
IF
limn→∞ (am,n) = bm
(uniformly by m)
limm→∞ (bm) = B
limm→∞ (am,n) = cn
(uniformly by n)
limn→∞ (cn) = C
THEN
B = C
Proof
Assume, B≠C and |B−C|=d.
Since limm→∞(bm)=B, there exists some natural number M1 such that
|B−bm| < d/4 for all m>M1
Since
limn→∞(am,n)=uniformly=bm
there exists some natural number N1 greater than M1 such that
|am,n−bm| < d/4 for all m,n>N1
Then, for all pairs m,n greater than N1 both following inequalities are true:
|B − bm| < d/4 and
|bm − am,n| < d/4
Therefore,
|B−am,n| < d/2
That is, our double sequence am,n with both indices m and n greater than N1 is closer to number B than d/2.
Let's use the same approach, but start from index n.
Since limn→∞(cn)=C, there exists some natural number N2 such that
|C−cn| < d/4 for all n>N2
Since
limm→∞(am,n)=uniformly=cn
there exists some natural number M2 greater than N2 such that
|am,n−cn| < d/4 for all m,n>M2
Then, for all pairs m,n greater than M2 both following inequalities are true:
|C − cn| < d/4 and
|cn − am,n| < d/4
Therefore,
|C−am,n| < d/2
That is, our double sequence am,n with both indices m and n greater than M2 is closer to number C than d/2.
Choosing K=max(N1,M2) we see that all am,n with indices greater than K should be closer to B than d/2 and at the same time should be closer to C than d/2.
With the distance between B and C equal to d it's impossible.
We came to contradiction that signifies that our initial assumption that B≠C is wrong.
Therefore, B=C.
For sequences that satisfy the conditions of the theorem above we can define their limit regardless of how we calculate it, starting from the first index or the second, and can combine indices in the notation
limm,n→∞ am,n = B
Not every sequence satisfies the conditions of this theorem.
For example, am,n=m/n has no unconditional limit.
If m is fixed and we vary n→∞, each bm is zero.
Hence, limm→∞ bm = 0
But if we fix n and vary m→∞, the resulting sequence {1/n,2/n,3/n...} has no limit for any n.
Double Limits
Sometimes we are interested in sequences that depend on two natural numbers like {am,n}.
For example,
am,n=arctan(m)+2−n.
Now, if m→∞ and n→∞, how to calculate the limit of am,n?
It might be
limm→∞ [limn→∞ (am,n)]
or
limn→∞ [limm→∞ (am,n)]
depending on which index, m or n, we will use to go to a limit first, and there is no guarantee that the answers will be the same.
Let's check both methods.
limn→∞ (am,n) =
= limn→∞ (arctan(m) + 2−n) =
= arctan(m)
limm→∞ (arctan(m)) = π/2
If we change the order of limits,
limm→∞ (am,n) =
= limm→∞ (arctan(m) + 2−n) =
= π/2 + 2−n
limn→∞ (π/2 + 2−n) = π/2
As you see, the results are the same.
In some way, the equality of these two limits might be considered similar to a standard accounting procedure of checking the calculations.
Imagine an M⨯N matrix with numbers.
If you summarize the numbers within each of M rows with row #i having a sum Ri and summarize all these row totals by i from 1 to M, you will get a total of all numbers in an original table.
If you summarize the numbers within each of N columns with column #j having a sum Sj and summarize all these column totals by j from 1 to N, you should get exactly the same total of all numbers.
If these two calculated totals are not equal, that is if
Σi∈[1,M] Ri ≠ Σj∈[1,N] Sj
then your calculations are wrong.
The equality of two limits in the example above is not coincidental. We shall prove it as the theorem below.
But, to make our proof rigorous, we have to make a short comment about uniform convergence.
We say that sequence {am,n} is converging uniformly by m to bm as n→∞ if for any positive ε there is number K such that
|bm−am,n| < ε
as long as both n and m are greater than K.
Analogously, we say that sequence {am,n} is converging uniformly by n to cn as m→∞ if for any positive ε there is number K such that
|cn−am,n| < ε
as long as both n and m are greater than K.
Theorem
IF
limn→∞ (am,n) = bm
(uniformly by m)
limm→∞ (bm) = B
limm→∞ (am,n) = cn
(uniformly by n)
limn→∞ (cn) = C
THEN
B = C
Proof
Assume, B≠C and |B−C|=d.
Since limm→∞(bm)=B, there exists some natural number M1 such that
|B−bm| < d/4 for all m>M1
Since
limn→∞(am,n)=uniformly=bm
there exists some natural number N1 greater than M1 such that
|am,n−bm| < d/4 for all m,n>N1
Then, for all pairs m,n greater than N1 both following inequalities are true:
|B − bm| < d/4 and
|bm − am,n| < d/4
Therefore,
|B−am,n| < d/2
That is, our double sequence am,n with both indices m and n greater than N1 is closer to number B than d/2.
Let's use the same approach, but start from index n.
Since limn→∞(cn)=C, there exists some natural number N2 such that
|C−cn| < d/4 for all n>N2
Since
limm→∞(am,n)=uniformly=cn
there exists some natural number M2 greater than N2 such that
|am,n−cn| < d/4 for all m,n>M2
Then, for all pairs m,n greater than M2 both following inequalities are true:
|C − cn| < d/4 and
|cn − am,n| < d/4
Therefore,
|C−am,n| < d/2
That is, our double sequence am,n with both indices m and n greater than M2 is closer to number C than d/2.
Choosing K=max(N1,M2) we see that all am,n with indices greater than K should be closer to B than d/2 and at the same time should be closer to C than d/2.
With the distance between B and C equal to d it's impossible.
We came to contradiction that signifies that our initial assumption that B≠C is wrong.
Therefore, B=C.
For sequences that satisfy the conditions of the theorem above we can define their limit regardless of how we calculate it, starting from the first index or the second, and can combine indices in the notation
limm,n→∞ am,n = B
Not every sequence satisfies the conditions of this theorem.
For example, am,n=m/n has no unconditional limit.
If m is fixed and we vary n→∞, each bm is zero.
Hence, limm→∞ bm = 0
But if we fix n and vary m→∞, the resulting sequence {1/n,2/n,3/n...} has no limit for any n.
Thursday, November 20, 2025
Physics+ Lagrangian in N Degrees of Freedom: UNIZOR.COM - Physics+ 4 All...
Notes to a video lecture on UNIZOR.COM
Lagrangian
for N-dimensional Systems
Background
In one of the previous lectures we considered a point-mass object oscillating on a spring in an empty one-dimensional space with Cartesian coordinates (one degree of freedom).
In that case we defined a Lagrangian of an object as a difference between its kinetic and potential energies and built a theory equivalent to Newtonian but based on the Euler-Lagrange equation instead of the Newton's Second Law.
In another lecture we discussed a spring pendulum (two degrees of freedom) and used non-Cartesian parameters to define a state of a system - an angle of pendulum from a vertical and a spring's length.
It was possible but rather complicated to use the Newtonian approach, so we applied Lagrangian Mechanics to come up with the differential equations to describe a state of this system.
An important reason for using Lagrangian Mechanics with energies instead of vectors of force and accelerations in that second example was that energies are scalars, while forces and accelerations are vectors.
Manipulations with scalars are simpler, especially dealing with complex systems with more than one degree of freedom.
Obviously, no matter how we solve a problem, the calculated actual physical trajectories of objects in space must be the same.
Before proceeding any further, we strongly recommend to refresh your knowledge about conservative forces, independence of work performed by these forces from a trajectory of an object moved by them, a concept of a field and its potential.
The chapter Laws of Newton of this course is a good source of this information.
Recall that conservative forces are defined as those that depend only on position in space. Their work, performed by moving an object from one position to another, does not depend on trajectory or speed along this trajectory, but depends only on the beginning and ending positions of an object.
From the Energy Conservation Law follows that the work performed by a conservative force that moves an object changes the potential energy of this object by the amount of work performed.
Consider an isolated closed system of N point-mass objects acting on each other with conservative forces and no forces from outside of this system.
The force on the ith object is
Fi = {Fix,Fiy,Fiz}.
If this force moved this object by an infinitesimal increment
dri = {dxi,dyi,dzi},
it performed some infinitesimal amount of work
dWi = (Fi · dri) =
= Fix·dxi+Fiy·dyi+Fiz·dzi
From the Energy Conservation Law follows that potential energy of this object Ui should diminish by this amount of work
dUi = −dWi
When all N objects are moved by corresponding forces, the total increment of potential energy of an entire system is
dU = −Σi∈[1,N]dWi =
= −Σi∈[1,N](Fi · dri) =
= −Σi∈[1,N](Fix·dxi+Fiy·dyi+Fiz·dzi)
From this equation follows the relationship between an increment of a total potential energy of an entire system and each individual force
Fix = −∂U/∂xi
Fiy = −∂U/∂yi
Fiz = −∂U/∂zi
Using vectors and operator
∇i = {∂/∂xi,∂/∂yi,∂/∂zi}
above equations can be expressed as
Fi = −∇iU
for all i∈[1,N]
Lagrangian Mechanics was invented to simplify analysis of complex systems acted upon by conservative forces, like electrostatic, gravitational or spring forces.
We are going to prove that Lagrangian Mechanics of a closed (no external forces) mechanical system with its components acted among themselves with some conservative forces produces differential equations of motion that are equivalent to Newtonian equations, but easier to deal with.
Consider a system that consists of N point-masses with each ith component Ωi acted upon by conservative forces from all components within this system.
The time-dependent Cartesian coordinates of each Ωi are {xi(t),yi(t),zi(t)}, which we will denote as a vector ri(t).
Let a combined conservative force acting on component Ωi that depends on positions of all components of a system be
Fi(r1,...rN)
The Newton's Second Law of motion for each object in a system is, therefore,
Fi(r1(t),...rN(t)) = mi·r"i(t)
where each Fi is a vector of three components {Fix,Fiy,Fiz}, and each component is a function of 3N coordinates of all objects in a system,
mass mi is a mass of Ωi and
a symbol " means the second derivative of position vector ri(t) of object Ωi by time, that is, its vector of acceleration{x"i(t),y"i(t),z"i(t)}.
In coordinate form the above equation can be written as
Fix(r1(t),...rN(t)) = mi·x"i(t)
Fiy(r1(t),...rN(t)) = mi·y"i(t)
Fiz(r1(t),...rN(t)) = mi·z"i(t)
In summary, we have 3N differential equations of 2-nd order, three for each component of a system of N objects.
In case of multiple objects in three-dimensional space exerting forces on each other (like all the planets of our Solar system or a nucleus with all its electrons in an atom) the vectors of forces are directed in different directions and the system of differential equations based on Newton's Second law is extremely complex.
Let's approach it differently.
Since all forces Fi are conservative, each one can be represented as
Fi(r1(t),...rN(t)) =
= −∇iU(r1(t),...rN(t))
where U(r1(t),...rN(t)) is a total potential energy of an entire system and
∇i is a vector of its partial derivatives by each coordinate of object Ωi.
∇i = {∂/∂xi,∂/∂yi,∂/∂zi}.
Let's shorten for convenience the results above as
Fi = −∇iU
and rewrite it in (x,y,z) components of Cartesian coordinates
Fix = −∂U/∂xi
Fiy = −∂U/∂yi
Fiz = −∂U/∂zi
As we see, knowing the potential energy of a system of objects is sufficient to know all the conservative forces acted on individual objects in this system.
The Newton's Second Law equation for object Ωi in vector form is
Fi(r1(t),...rN(t)) = mi·r"i(t)
which in coordinate form would be
Fix(x1(t),...zN(t)) = mi·x"i(t)
Fiy(x1(t),...zN(t)) = mi·y"i(t)
Fiz(x1(t),...zN(t)) = mi·z"i(t)
Using the potential energy, the same equations for object Ωi would be
−∂U /∂xi = mi·x"i(t)
−∂U /∂yi = mi·y"i(t)
−∂U /∂zi = mi·z"i(t)
where U=U(x1(t),...zN(t)) is a total potential energy of an entire system.
Let's address the mi·r"i(t) side of the Newton's Second Law and derive its value from the kinetic energy of an object Ωi.
We express a vector r"i(t) in (x,y,z) coordinates as
(x"i(t),y"i(t),z"i(t))
Kinetic energy of Ωi equals to Ki(t)=½mi·vi(t)² where vi is a linear speed along a trajectory
vi(t)² = r'i(t)·r'i(t) =
= x'i(t)²+y'i(t)²+z'i(t)²
Now we can express the components of an acceleration vector r"i(t) of Ωi in terms of its kinetic energy
Ki(t)=½mi·[x'i(t)²+y'i(t)²+z'i(t)²]
Partial derivatives of kinetic energy by each coordinate of velocity vector produces coordinates of an object's momentum
∂Ki /∂x'i = mi·x'i
∂Ki /∂y'i = mi·y'i
∂Ki /∂z'i = mi·z'i
Derivative by time of a momentum gives the right side of the Newton's Second Law d/dt ∂Ki /∂x'i = d/dt mi·x'i =
= mi·x"i
d/dt ∂Ki /∂y'i = d/dt mi·y'i =
= mi·y"i
d/dt ∂Ki /∂z'i = d/dt mi·z'i =
= mi·z"i
We are ready to express the Newton's Second Law in terms of kinetic and potential energy.
From
−∂U /∂xi = mi·x"i
and
d/dt ∂Ki /∂x'i = mi·x"i
follows
−∂U/∂xi = d/dt ∂Ki /∂x'i
Similarly,
−∂U /∂yi = d/dt ∂Ki /∂y'i
−∂U/∂zi = d/dt ∂Ki /∂z'i
The total kinetic energy of a system is a sum of kinetic energies of its components
K = K1+...+KN
Since each Ki depends only on a velocity of the ith object{x'i(t),y'i(t),z'i(t)} ,
partial derivative of Ki by x'i(t), y'i(t) or by z'i(t) is the same as partial derivatives of an entire kinetic energy of a system K by the same components x'i(t), y'i(t) or z'i(t) of the velocity of the ith object
∂Ki /∂x'i = ∂K/∂x'i
∂Ki /∂y'i = ∂K/∂y'i
∂Ki /∂z'i = ∂K/∂z'i
Using total kinetic energy of a system, the formulas describing the laws of motion of object Ωi would be
−∂U/∂xi = d/dt ∂K/∂x'i
−∂U/∂yi = d/dt ∂K/∂y'i
−∂U/∂zi = d/dt ∂K/∂z'i
Now the only participants in these equations are the total kinetic and potential energies of an entire system - just two numbers that depend on positions and velocities of system's components.
To make the theory more elegant, let's introduce a Lagrangian L=K−U that equals to a difference between kinetic and potential energy of this system.
Since kinetic energy of a system K is independent of positions of its components{xi(t),yi(t),zi(t)} ,
−∂U/∂xi=∂(K−U)/∂xi=∂L/∂xi
and similar with partial derivatives by yi and zi.
Since potential energy of a system U is independent on velocities of its components,
∂K/∂x'i=∂(K−U)/∂x'i=∂L/∂x'i
and similar with partial derivatives by yi and zi.
Therefore, our equations look even simpler
∂L/∂xi = d/dt ∂L/∂x'i
∂L/∂yi = d/dt ∂L/∂y'i
∂L/∂zi = d/dt ∂L/∂z'i
The equations above are also differential equations of the second order, like with Newton's Second Law.
There are also 3N of these equations (three coordinates for N objects in a system).
But there is only one number, Lagrangian, also called action, a function of all positions and velocities, to deal with for all objects instead of individual forces for each object.
Lagrangian Mechanics allows to deal with complex system in a simpler way.
As the cherry on top, consider the same equations in the form
d/dt ∂L/∂x'i − ∂L/∂xi = 0
d/dt ∂L/∂y'i − ∂L/∂yi = 0
d/dt ∂L/∂z'i − ∂L/∂zi = 0
In these equations Lagrangian L depends on 3N parameters, positions and velocities of N components of our system, which are, in turn, time-dependent.
So, ultimately, Lagrangian L is a function of time.
On one hand, these are equations that define a motion of a system, that is they define a trajectory of a system changing positions and velocities of its components from one moment in time to another.
On another hand, as we discussed in the Variations chapter of this course, they produce a function of time L(t) that brings to extremum (usually, minimum) the action functional
S = ∫[t1,t2] L(t)·dt
Therefore, we can say that a mechanical system with only conservative forces present changes its state along anN-dimensional trajectory that minimizes the action functional above.
Lagrangian
for N-dimensional Systems
Background
In one of the previous lectures we considered a point-mass object oscillating on a spring in an empty one-dimensional space with Cartesian coordinates (one degree of freedom).
In that case we defined a Lagrangian of an object as a difference between its kinetic and potential energies and built a theory equivalent to Newtonian but based on the Euler-Lagrange equation instead of the Newton's Second Law.
In another lecture we discussed a spring pendulum (two degrees of freedom) and used non-Cartesian parameters to define a state of a system - an angle of pendulum from a vertical and a spring's length.
It was possible but rather complicated to use the Newtonian approach, so we applied Lagrangian Mechanics to come up with the differential equations to describe a state of this system.
An important reason for using Lagrangian Mechanics with energies instead of vectors of force and accelerations in that second example was that energies are scalars, while forces and accelerations are vectors.
Manipulations with scalars are simpler, especially dealing with complex systems with more than one degree of freedom.
Obviously, no matter how we solve a problem, the calculated actual physical trajectories of objects in space must be the same.
Before proceeding any further, we strongly recommend to refresh your knowledge about conservative forces, independence of work performed by these forces from a trajectory of an object moved by them, a concept of a field and its potential.
The chapter Laws of Newton of this course is a good source of this information.
Recall that conservative forces are defined as those that depend only on position in space. Their work, performed by moving an object from one position to another, does not depend on trajectory or speed along this trajectory, but depends only on the beginning and ending positions of an object.
From the Energy Conservation Law follows that the work performed by a conservative force that moves an object changes the potential energy of this object by the amount of work performed.
Consider an isolated closed system of N point-mass objects acting on each other with conservative forces and no forces from outside of this system.
The force on the ith object is
Fi = {Fix,Fiy,Fiz}.
If this force moved this object by an infinitesimal increment
dri = {dxi,dyi,dzi},
it performed some infinitesimal amount of work
dWi = (Fi · dri) =
= Fix·dxi+Fiy·dyi+Fiz·dzi
From the Energy Conservation Law follows that potential energy of this object Ui should diminish by this amount of work
dUi = −dWi
When all N objects are moved by corresponding forces, the total increment of potential energy of an entire system is
dU = −Σi∈[1,N]dWi =
= −Σi∈[1,N](Fi · dri) =
= −Σi∈[1,N](Fix·dxi+Fiy·dyi+Fiz·dzi)
From this equation follows the relationship between an increment of a total potential energy of an entire system and each individual force
Fix = −∂U/∂xi
Fiy = −∂U/∂yi
Fiz = −∂U/∂zi
Using vectors and operator
∇i = {∂/∂xi,∂/∂yi,∂/∂zi}
above equations can be expressed as
Fi = −∇iU
for all i∈[1,N]
Lagrangian Mechanics was invented to simplify analysis of complex systems acted upon by conservative forces, like electrostatic, gravitational or spring forces.
We are going to prove that Lagrangian Mechanics of a closed (no external forces) mechanical system with its components acted among themselves with some conservative forces produces differential equations of motion that are equivalent to Newtonian equations, but easier to deal with.
Consider a system that consists of N point-masses with each ith component Ωi acted upon by conservative forces from all components within this system.
The time-dependent Cartesian coordinates of each Ωi are {xi(t),yi(t),zi(t)}, which we will denote as a vector ri(t).
Let a combined conservative force acting on component Ωi that depends on positions of all components of a system be
Fi(r1,...rN)
The Newton's Second Law of motion for each object in a system is, therefore,
Fi(r1(t),...rN(t)) = mi·r"i(t)
where each Fi is a vector of three components {Fix,Fiy,Fiz}, and each component is a function of 3N coordinates of all objects in a system,
mass mi is a mass of Ωi and
a symbol " means the second derivative of position vector ri(t) of object Ωi by time, that is, its vector of acceleration
In coordinate form the above equation can be written as
Fix(r1(t),...rN(t)) = mi·x"i(t)
Fiy(r1(t),...rN(t)) = mi·y"i(t)
Fiz(r1(t),...rN(t)) = mi·z"i(t)
In summary, we have 3N differential equations of 2-nd order, three for each component of a system of N objects.
In case of multiple objects in three-dimensional space exerting forces on each other (like all the planets of our Solar system or a nucleus with all its electrons in an atom) the vectors of forces are directed in different directions and the system of differential equations based on Newton's Second law is extremely complex.
Let's approach it differently.
Since all forces Fi are conservative, each one can be represented as
Fi(r1(t),...rN(t)) =
= −∇iU(r1(t),...rN(t))
where U(r1(t),...rN(t)) is a total potential energy of an entire system and
∇i is a vector of its partial derivatives by each coordinate of object Ωi.
∇i = {∂/∂xi,∂/∂yi,∂/∂zi}.
Let's shorten for convenience the results above as
Fi = −∇iU
and rewrite it in (x,y,z) components of Cartesian coordinates
Fix = −∂U/∂xi
Fiy = −∂U/∂yi
Fiz = −∂U/∂zi
As we see, knowing the potential energy of a system of objects is sufficient to know all the conservative forces acted on individual objects in this system.
The Newton's Second Law equation for object Ωi in vector form is
Fi(r1(t),...rN(t)) = mi·r"i(t)
which in coordinate form would be
Fix(x1(t),...zN(t)) = mi·x"i(t)
Fiy(x1(t),...zN(t)) = mi·y"i(t)
Fiz(x1(t),...zN(t)) = mi·z"i(t)
Using the potential energy, the same equations for object Ωi would be
−∂U /∂xi = mi·x"i(t)
−∂U /∂yi = mi·y"i(t)
−∂U /∂zi = mi·z"i(t)
where U=U(x1(t),...zN(t)) is a total potential energy of an entire system.
Let's address the mi·r"i(t) side of the Newton's Second Law and derive its value from the kinetic energy of an object Ωi.
We express a vector r"i(t) in (x,y,z) coordinates as
(x"i(t),y"i(t),z"i(t))
Kinetic energy of Ωi equals to Ki(t)=½mi·vi(t)² where vi is a linear speed along a trajectory
vi(t)² = r'i(t)·r'i(t) =
= x'i(t)²+y'i(t)²+z'i(t)²
Now we can express the components of an acceleration vector r"i(t) of Ωi in terms of its kinetic energy
Ki(t)=½mi·[x'i(t)²+y'i(t)²+z'i(t)²]
Partial derivatives of kinetic energy by each coordinate of velocity vector produces coordinates of an object's momentum
∂Ki /∂x'i = mi·x'i
∂Ki /∂y'i = mi·y'i
∂Ki /∂z'i = mi·z'i
Derivative by time of a momentum gives the right side of the Newton's Second Law d/dt ∂Ki /∂x'i = d/dt mi·x'i =
= mi·x"i
d/dt ∂Ki /∂y'i = d/dt mi·y'i =
= mi·y"i
d/dt ∂Ki /∂z'i = d/dt mi·z'i =
= mi·z"i
We are ready to express the Newton's Second Law in terms of kinetic and potential energy.
From
−∂U /∂xi = mi·x"i
and
d/dt ∂Ki /∂x'i = mi·x"i
follows
−∂U/∂xi = d/dt ∂Ki /∂x'i
Similarly,
−∂U /∂yi = d/dt ∂Ki /∂y'i
−∂U/∂zi = d/dt ∂Ki /∂z'i
The total kinetic energy of a system is a sum of kinetic energies of its components
K = K1+...+KN
Since each Ki depends only on a velocity of the ith object
∂Ki /∂x'i = ∂K/∂x'i
∂Ki /∂y'i = ∂K/∂y'i
∂Ki /∂z'i = ∂K/∂z'i
Using total kinetic energy of a system, the formulas describing the laws of motion of object Ωi would be
−∂U/∂xi = d/dt ∂K/∂x'i
−∂U/∂yi = d/dt ∂K/∂y'i
−∂U/∂zi = d/dt ∂K/∂z'i
Now the only participants in these equations are the total kinetic and potential energies of an entire system - just two numbers that depend on positions and velocities of system's components.
To make the theory more elegant, let's introduce a Lagrangian L=K−U that equals to a difference between kinetic and potential energy of this system.
Since kinetic energy of a system K is independent of positions of its components
−∂U/∂xi=∂(K−U)/∂xi=∂L/∂xi
and similar with partial derivatives by yi and zi.
Since potential energy of a system U is independent on velocities of its components,
∂K/∂x'i=∂(K−U)/∂x'i=∂L/∂x'i
and similar with partial derivatives by yi and zi.
Therefore, our equations look even simpler
∂L/∂xi = d/dt ∂L/∂x'i
∂L/∂yi = d/dt ∂L/∂y'i
∂L/∂zi = d/dt ∂L/∂z'i
The equations above are also differential equations of the second order, like with Newton's Second Law.
There are also 3N of these equations (three coordinates for N objects in a system).
But there is only one number, Lagrangian, also called action, a function of all positions and velocities, to deal with for all objects instead of individual forces for each object.
Lagrangian Mechanics allows to deal with complex system in a simpler way.
As the cherry on top, consider the same equations in the form
d/dt ∂L/∂x'i − ∂L/∂xi = 0
d/dt ∂L/∂y'i − ∂L/∂yi = 0
d/dt ∂L/∂z'i − ∂L/∂zi = 0
In these equations Lagrangian L depends on 3N parameters, positions and velocities of N components of our system, which are, in turn, time-dependent.
So, ultimately, Lagrangian L is a function of time.
On one hand, these are equations that define a motion of a system, that is they define a trajectory of a system changing positions and velocities of its components from one moment in time to another.
On another hand, as we discussed in the Variations chapter of this course, they produce a function of time L(t) that brings to extremum (usually, minimum) the action functional
S = ∫[t1,t2] L(t)·dt
Therefore, we can say that a mechanical system with only conservative forces present changes its state along an
Sunday, September 21, 2025
Physics+ N-dimensional Lagrangian: UNIZOR.COM - Physics+ 4 All - Lagrangian
Notes to a video lecture on UNIZOR.COM
Lagrangian
for N-dimensional Systems
In one of the previous lectures we considered a point-mass object oscillating on a spring in an empty one-dimensional space with Cartesian coordinates (one degree of freedom).
In that case we defined a Lagrangian of an object as a difference between its kinetic and potential energies and built a theory equivalent to Newtonian but based on the Euler-Lagrange equation instead of the Newton's Second Law.
In another lecture we discussed a spring pendulum (two degrees of freedom) and used non-Cartesian parameters to define a state of a system - an angle of pendulum from a vertical and a spring's length.
It was possible but rather complicated to use the Newtonian approach, so we applied Lagrangian Mechanics to come up with the differential equations to describe a state of this system.
An important reason for using energies instead of vectors of force and acceleration in that second example was that energies are scalars, while forces and accelerations are vectors.
Manipulations with scalars are simpler, especially dealing with complex systems with more than one degree of freedom.
Obviously, no matter how we solve a problem, the calculated actual physical trajectories of objects in space must be the same.
Before proceeding any further, we strongly recommend to refresh your knowledge about conservative forces, independence of work performed by these forces from a trajectory of an object moved by them, a concept of a field and its potential.
The chapter Laws of Newton of this course is a good source of this information.
Recall that conservative forces are defined as those that depend only on position in space, independent of time. Their work, performed by moving an object from one position to another, does not depend on trajectory or speed along this trajectory, but depends only on the beginning and ending positions of an object.
From the Energy Conservation Law follows that the work performed by a conservative force that moves an object changes the potential energy of this object by the amount of work performed.
Recall that an increment of potential energy
ΔEpot=Epot(P2)−Epot(P1)
of an object moved by a conservative force F (a force of a field, a force of a spring etc.) from position P1 to P2 along any trajectory equals to the work performed by this conservative force.
ΔEpot = ∫[P1~P2]F(P)·dr
where P is a variable position of an object moving along a trajectory from P1 to P2,
r=OP is a vector from the origin of coordinates O to a position of an object P as it moves along a trajectory,
multiplication F(P)·dr is a scalar product of two vectors - a vector of force and an infinitesimal vector of increment of a position of an object along its trajectory and
[P1~P2] denotes that an integral is taken along a trajectory from P1 to P2.
The same conservative force (a force of a field, a force of a spring etc.) can be represented as a vector of gradient of a potential
F = −∇Epot
where a minus sign '−' indicates that the conservative force (a force of a field, a force of a spring etc.) is always directed towards decreasing of potential.
Lagrangian Mechanics was invented to simplify analysis of complex systems acted upon by conservative forces, like electrostatic, gravitational or spring forces.
We are going to prove that Lagrangian Mechanics of a closed (no external forces) mechanical system with its components acted among themselves with some conservative forces produces differential equations of motion that are equivalent to Newtonian equations, but easier to deal with.
Consider a system that consists of N point-masses with each ith component Ωi acted upon by conservative forces (three-dimensional vectors) from all components of this system with a combined force
Fi(r1,...rN)
that depends on positions of all components of a system.
The time-dependent Cartesian coordinates of each Ωi are {xi(t),yi(t),zi(t)}, which we will denote as a vector ri(t).
The Newton's Second Law of motion for each object in a system is, therefore,
Fi(r1(t),...rN(t)) = mi·r"i(t)
where each Fi is a vector of three components {Fix,Fiy,Fiz}, and each component is a function of 3N coordinates of all objects in a system,
mass mi is a mass of Ωi and
a symbol " means the second derivative of position vector ri(t) of object Ωi by time, that is, its vector of acceleration{x"i(t),y"i(t),z"i(t)}.
In coordinate form the above equation can be written as
Fix(r1(t),...rN(t)) = mi·x"i(t)
Fiy(r1(t),...rN(t)) = mi·y"i(t)
Fiz(r1(t),...rN(t)) = mi·z"i(t)
In summary, we have 3N differential equations of 2-nd order, three for each component of a system of N objects.
In case of multiple objects in three-dimensional space exerting forces on each other (like all the planets of our Solar system or a nucleus with all its electrons in an atom) the vectors of forces are directed in different directions and the system of differential equations based on Newton's Second law is extremely complex.
Let's approach it differently.
Since all forces Fi are conservative, each one can be represented as
Fi(r1(t),...rN(t)) =
= −∇iU(r1(t),...rN(t))
where U(r1(t),...rN(t)) is a total potential of an entire system and
∇i is a vector of its partial derivatives by each coordinate of object Ωi.
∇i = {∂/∂xi,∂/∂yi,∂/∂zi}.
Let's shorten for convenience the results above as
Fi = −∇iU
and rewrite it in (x,y,z) components of Cartesian coordinates
Fix = −∂U/∂xi
Fiy = −∂U/∂yi
Fiz = −∂U/∂zi
As we see, knowing the potential of a system of objects at each point is sufficient to know all the conservative forces acted on individual objects in this system.
Let's address the mi·r"i(t) side of the Newton's Second Law and derive its value from the kinetic energy of an object Ωi.
We express a vector r"i(t) in (x,y,z) coordinates as
(x"i(t),y"i(t),z"i(t))
The Newton's Second Law equations for object Ωi in coordinate form would then be
Fix = mi·x"i(t)
Fiy = mi·y"i(t)
Fiz = mi·z"i(t)
Using the potential energy, the same equations for object Ωi would be
−∂U /∂x = mi·x"i(t)
−∂U /∂y = mi·y"i(t)
−∂U /∂z = mi·z"i(t)
Kinetic energy of Ωi equals to Ki(t)=½mi·vi(t)² where vi is a linear speed along a trajectory
vi(t)² = r'i(t)·r'i(t) =
= x'i(t)²+y'i(t)²+z'i(t)²
Now we can express the components of an acceleration vector r"i(t) of Ωi in terms of its kinetic energy
Ki(t)=½mi·[x'i(t)²+y'i(t)²+z'i(t)²]
Partial derivatives of kinetic energy by each coordinate of velocity vector produces coordinates of an object's momentum
∂Ki /∂x'i = m·x'i
∂Ki /∂y'i = m·y'i
∂Ki /∂z'i = m·z'i
Derivative by time of a momentum gives the right side of the Newton's Second Law d/dt ∂Ki /∂x'i=d/dt m·x'i=m·x"i
d/dt ∂Ki /∂y'i=d/dt m·y'i=m·y"i
d/dt ∂Ki /∂z'i=d/dt m·z'i=m·z"i
We are ready to express the Newton's Second Law in terms of kinetic and potential energy.
From
Fix = −∂U/∂xi
and
d/dt ∂Ki /∂x'i = m·x"i
follows
−∂U/∂xi = d/dt ∂Ki /∂x'i
Similarly,
−∂U /∂yi = d/dt ∂Ki /∂y'i
−∂U/∂zi = d/dt ∂Ki /∂z'i
The total kinetic energy of a system is a sum of kinetic energies of its components
K = K1+...+KN
Since each Ki depends only on a velocity of the ith object{x'i(t),y'i(t),z'i(t)} ,
partial derivative of Ki by x'i(t), y'i(t) or by z'i(t) is the same as partial derivatives of an entire kinetic energy of a system K by the same components x'i(t), y'i(t) or z'i(t) of the velocity of the ith object
∂Ki /∂x'i = ∂K/∂x'i
∂Ki /∂y'i = ∂K/∂y'i
∂Ki /∂z'i = ∂K/∂z'i
Using total kinetic energy of a system, the formulas describing the laws of motion of object Ωi would be
−∂U/∂xi = d/dt ∂K/∂x'i
−∂U/∂yi = d/dt ∂K/∂y'i
−∂U/∂zi = d/dt ∂K/∂z'i
Now the only participants in these equations are the total kinetic and potential energies of an entire system - just two numbers that depend on positions and velocities of system's components.
To make the theory more elegant, let's introduce a Lagrangian L=K−U that equals to a difference between kinetic and potential energy of this system.
Since kinetic energy of a system K is independent of positions of its components{xi(t),yi(t),zi(t)} ,
−∂U/∂xi=∂(K−U)/∂xi=∂L/∂xi
and similar with partial derivatives by yi and zi.
Since potential energy of a system U is independent on velocities of its components,
∂K/∂x'i=∂(K−U)/∂x'i=∂L/∂x'i
and similar with partial derivatives by yi and zi.
Therefore, our equations look even simpler
∂L/∂xi = d/dt ∂L/∂x'i
∂L/∂yi = d/dt ∂L/∂y'i
∂L/∂zi = d/dt ∂L/∂z'i
The equations above are also differential equations of the second order, like withNewton's Second Law.
There are also 3N of these equations (three coordinates for N objects in a system).
But there is only one number, Lagrangian, also called action, a function of all positions and velocities, to deal with for all objects instead of individual forces for each object.
Lagrangian Mechanics allows to deal with complex system in a simpler way.
As the cherry on top, consider the same equations in the form
d/dt ∂L/∂x'i − ∂L/∂xi = 0
d/dt ∂L/∂y'i − ∂L/∂yi = 0
d/dt ∂L/∂z'i − ∂L/∂zi = 0
In these equations Lagrangian L depends on 3N parameters, positions and velocities of N components of our system, which are, in turn, are time-dependent.
So, ultimately, Lagrangian L is a function of time.
On one hand, these are equations that define a motion of a system, that is they define a trajectory of a system changing positions and velocities of its components from one moment in time to another.
On another hand, as we discussed in the Variations chapter of this course, they produce a function of time L(t) that brings to extremum (usually, minimum) the action functional
S = ∫[t1,t2] L(t)·dt
Therefore, we can say that a mechanical system with only conservative forces present changes its state along anN-dimensional trajectory that minimizes the action functional above.
Lagrangian
for N-dimensional Systems
In one of the previous lectures we considered a point-mass object oscillating on a spring in an empty one-dimensional space with Cartesian coordinates (one degree of freedom).
In that case we defined a Lagrangian of an object as a difference between its kinetic and potential energies and built a theory equivalent to Newtonian but based on the Euler-Lagrange equation instead of the Newton's Second Law.
In another lecture we discussed a spring pendulum (two degrees of freedom) and used non-Cartesian parameters to define a state of a system - an angle of pendulum from a vertical and a spring's length.
It was possible but rather complicated to use the Newtonian approach, so we applied Lagrangian Mechanics to come up with the differential equations to describe a state of this system.
An important reason for using energies instead of vectors of force and acceleration in that second example was that energies are scalars, while forces and accelerations are vectors.
Manipulations with scalars are simpler, especially dealing with complex systems with more than one degree of freedom.
Obviously, no matter how we solve a problem, the calculated actual physical trajectories of objects in space must be the same.
Before proceeding any further, we strongly recommend to refresh your knowledge about conservative forces, independence of work performed by these forces from a trajectory of an object moved by them, a concept of a field and its potential.
The chapter Laws of Newton of this course is a good source of this information.
Recall that conservative forces are defined as those that depend only on position in space, independent of time. Their work, performed by moving an object from one position to another, does not depend on trajectory or speed along this trajectory, but depends only on the beginning and ending positions of an object.
From the Energy Conservation Law follows that the work performed by a conservative force that moves an object changes the potential energy of this object by the amount of work performed.
Recall that an increment of potential energy
ΔEpot=Epot(P2)−Epot(P1)
of an object moved by a conservative force F (a force of a field, a force of a spring etc.) from position P1 to P2 along any trajectory equals to the work performed by this conservative force.
ΔEpot = ∫[P1~P2]F(P)·dr
where P is a variable position of an object moving along a trajectory from P1 to P2,
r=OP is a vector from the origin of coordinates O to a position of an object P as it moves along a trajectory,
multiplication F(P)·dr is a scalar product of two vectors - a vector of force and an infinitesimal vector of increment of a position of an object along its trajectory and
[P1~P2] denotes that an integral is taken along a trajectory from P1 to P2.
The same conservative force (a force of a field, a force of a spring etc.) can be represented as a vector of gradient of a potential
F = −∇Epot
where a minus sign '−' indicates that the conservative force (a force of a field, a force of a spring etc.) is always directed towards decreasing of potential.
Lagrangian Mechanics was invented to simplify analysis of complex systems acted upon by conservative forces, like electrostatic, gravitational or spring forces.
We are going to prove that Lagrangian Mechanics of a closed (no external forces) mechanical system with its components acted among themselves with some conservative forces produces differential equations of motion that are equivalent to Newtonian equations, but easier to deal with.
Consider a system that consists of N point-masses with each ith component Ωi acted upon by conservative forces (three-dimensional vectors) from all components of this system with a combined force
Fi(r1,...rN)
that depends on positions of all components of a system.
The time-dependent Cartesian coordinates of each Ωi are {xi(t),yi(t),zi(t)}, which we will denote as a vector ri(t).
The Newton's Second Law of motion for each object in a system is, therefore,
Fi(r1(t),...rN(t)) = mi·r"i(t)
where each Fi is a vector of three components {Fix,Fiy,Fiz}, and each component is a function of 3N coordinates of all objects in a system,
mass mi is a mass of Ωi and
a symbol " means the second derivative of position vector ri(t) of object Ωi by time, that is, its vector of acceleration
In coordinate form the above equation can be written as
Fix(r1(t),...rN(t)) = mi·x"i(t)
Fiy(r1(t),...rN(t)) = mi·y"i(t)
Fiz(r1(t),...rN(t)) = mi·z"i(t)
In summary, we have 3N differential equations of 2-nd order, three for each component of a system of N objects.
In case of multiple objects in three-dimensional space exerting forces on each other (like all the planets of our Solar system or a nucleus with all its electrons in an atom) the vectors of forces are directed in different directions and the system of differential equations based on Newton's Second law is extremely complex.
Let's approach it differently.
Since all forces Fi are conservative, each one can be represented as
Fi(r1(t),...rN(t)) =
= −∇iU(r1(t),...rN(t))
where U(r1(t),...rN(t)) is a total potential of an entire system and
∇i is a vector of its partial derivatives by each coordinate of object Ωi.
∇i = {∂/∂xi,∂/∂yi,∂/∂zi}.
Let's shorten for convenience the results above as
Fi = −∇iU
and rewrite it in (x,y,z) components of Cartesian coordinates
Fix = −∂U/∂xi
Fiy = −∂U/∂yi
Fiz = −∂U/∂zi
As we see, knowing the potential of a system of objects at each point is sufficient to know all the conservative forces acted on individual objects in this system.
Let's address the mi·r"i(t) side of the Newton's Second Law and derive its value from the kinetic energy of an object Ωi.
We express a vector r"i(t) in (x,y,z) coordinates as
(x"i(t),y"i(t),z"i(t))
The Newton's Second Law equations for object Ωi in coordinate form would then be
Fix = mi·x"i(t)
Fiy = mi·y"i(t)
Fiz = mi·z"i(t)
Using the potential energy, the same equations for object Ωi would be
−∂U /∂x = mi·x"i(t)
−∂U /∂y = mi·y"i(t)
−∂U /∂z = mi·z"i(t)
Kinetic energy of Ωi equals to Ki(t)=½mi·vi(t)² where vi is a linear speed along a trajectory
vi(t)² = r'i(t)·r'i(t) =
= x'i(t)²+y'i(t)²+z'i(t)²
Now we can express the components of an acceleration vector r"i(t) of Ωi in terms of its kinetic energy
Ki(t)=½mi·[x'i(t)²+y'i(t)²+z'i(t)²]
Partial derivatives of kinetic energy by each coordinate of velocity vector produces coordinates of an object's momentum
∂Ki /∂x'i = m·x'i
∂Ki /∂y'i = m·y'i
∂Ki /∂z'i = m·z'i
Derivative by time of a momentum gives the right side of the Newton's Second Law d/dt ∂Ki /∂x'i=d/dt m·x'i=m·x"i
d/dt ∂Ki /∂y'i=d/dt m·y'i=m·y"i
d/dt ∂Ki /∂z'i=d/dt m·z'i=m·z"i
We are ready to express the Newton's Second Law in terms of kinetic and potential energy.
From
Fix = −∂U/∂xi
and
d/dt ∂Ki /∂x'i = m·x"i
follows
−∂U/∂xi = d/dt ∂Ki /∂x'i
Similarly,
−∂U /∂yi = d/dt ∂Ki /∂y'i
−∂U/∂zi = d/dt ∂Ki /∂z'i
The total kinetic energy of a system is a sum of kinetic energies of its components
K = K1+...+KN
Since each Ki depends only on a velocity of the ith object
∂Ki /∂x'i = ∂K/∂x'i
∂Ki /∂y'i = ∂K/∂y'i
∂Ki /∂z'i = ∂K/∂z'i
Using total kinetic energy of a system, the formulas describing the laws of motion of object Ωi would be
−∂U/∂xi = d/dt ∂K/∂x'i
−∂U/∂yi = d/dt ∂K/∂y'i
−∂U/∂zi = d/dt ∂K/∂z'i
Now the only participants in these equations are the total kinetic and potential energies of an entire system - just two numbers that depend on positions and velocities of system's components.
To make the theory more elegant, let's introduce a Lagrangian L=K−U that equals to a difference between kinetic and potential energy of this system.
Since kinetic energy of a system K is independent of positions of its components
−∂U/∂xi=∂(K−U)/∂xi=∂L/∂xi
and similar with partial derivatives by yi and zi.
Since potential energy of a system U is independent on velocities of its components,
∂K/∂x'i=∂(K−U)/∂x'i=∂L/∂x'i
and similar with partial derivatives by yi and zi.
Therefore, our equations look even simpler
∂L/∂xi = d/dt ∂L/∂x'i
∂L/∂yi = d/dt ∂L/∂y'i
∂L/∂zi = d/dt ∂L/∂z'i
The equations above are also differential equations of the second order, like withNewton's Second Law.
There are also 3N of these equations (three coordinates for N objects in a system).
But there is only one number, Lagrangian, also called action, a function of all positions and velocities, to deal with for all objects instead of individual forces for each object.
Lagrangian Mechanics allows to deal with complex system in a simpler way.
As the cherry on top, consider the same equations in the form
d/dt ∂L/∂x'i − ∂L/∂xi = 0
d/dt ∂L/∂y'i − ∂L/∂yi = 0
d/dt ∂L/∂z'i − ∂L/∂zi = 0
In these equations Lagrangian L depends on 3N parameters, positions and velocities of N components of our system, which are, in turn, are time-dependent.
So, ultimately, Lagrangian L is a function of time.
On one hand, these are equations that define a motion of a system, that is they define a trajectory of a system changing positions and velocities of its components from one moment in time to another.
On another hand, as we discussed in the Variations chapter of this course, they produce a function of time L(t) that brings to extremum (usually, minimum) the action functional
S = ∫[t1,t2] L(t)·dt
Therefore, we can say that a mechanical system with only conservative forces present changes its state along an
Saturday, August 23, 2025
Physics+ Pendulum in Lagrangian Mechanics: UNIZOR.COM - Physics+ 4 All -...
Notes to a video lecture on UNIZOR.COM
Mathematical Pendulum
Plain Pendulum
We will illustrate the application of Lagrangian mechanics by analyzing the movement of a mathematical pendulum - a problem we have already discussed in the Physics 4 Teens - Mechanics - Pendulum, Spring - Pendulum using the Newtonian approach.
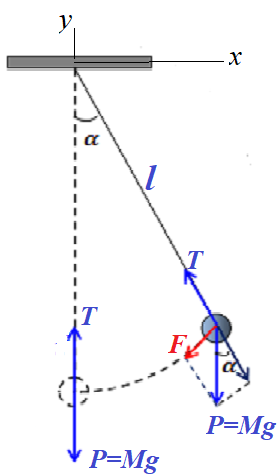
We recommend reviewing the lecture mentioned above and refresh the Newtonian method of deriving the main equation of motion of the pendulum:
α"(t) = −(g/l)·sin(α(t))
which was obtained from properly determining the force F that moves a pendulum as a vector sum of the gravity force directed vertically down and the tension of an unstretchable thread that keeps an object at the free end of a thread on a constant distance from the fixed end of a thread.
The two forces involved in formation of a resulting force F, gravity P=m·g and tension of a thread T, had to be combined using the rules for addition of vectors, which required some thinking.
Let's apply the Lagrangian mechanics to this problem using an angle of a thread with a vertical α as the one and only parameter that determines a position of an object.
This way of identification of a position is more convenient than Cartesian coordinates originated at the fixed end of a thread because both of them can be easily derived from α
x = l·sin(α)
y = −l·cos(α)
The Lagrangian is the difference between kinetic and potential energies.
L(α(t),α'(t)) =
= Ekin(α'(t)) − Epot(α(t))
Kinetic energy depends on mass M and linear speed of an object along its circular trajectory v=l·α'(t)
Ekin = ½M·v² =
= ½M·l²·[α'(t)]²
Potential energy depends on a mass of an object M, its height over the ground h(t) and an acceleration of free fall g.
Epot(t) = M·g·h(t)
If the origin of our coordinates, the fixed end of a thread, is at height H over the ground,
h = H − l·cos(α)
and, therefore,
Epot(t) = M·g·[H−l·cos(α(t))]
Now we can construct the Euler-Lagrange equation
(∂/∂α)L(α(t),α'(t)) =
= (d/dt)(∂/∂α')L(α(t),α'(t))
Calculate left and right sides separately.
(∂/∂α)L(α(t),α'(t)) =
= (∂/∂α)[Ekin(α'(t)) − Epot(α(t))] =
= (∂/∂α)[−Epot(α(t))] =
= (∂/∂α)[−M·g·[H−l·cos(α(t))]] =
= −M·g·l·sin(α(t))
(d/dt)(∂/∂α')L(α(t),α'(t)) =
=(d/dt)(∂/∂α')[Ekin(α'(t))−Epot(α(t))]=
= (d/dt)(∂/∂α')Ekin(α'(t)) =
= (d/dt)(∂/∂α')½M·l²·[α'(t)]² =
= (d/dt)M·l²·α'(t) =
= M·l²·α"(t)
The Euler-Lagrange equation is
−M·g·l·sin(α(t)) = M·l²·α"(t)
or
α"(t) = −(g/l)·sin(α(t))
which is exactly as applying Newtonian mechanics.
If you don't think the Lagrangian mechanics is simpler than Newtonian for those who are familiar with Calculus of partial derivatives, consider the next example.
Spring Pendulum
A weightless spring replaces an unstretchable thread of the previous problem.
The spring and an object on its end are in a weightless frictionless tube that maintains a straight form, so an object has two degrees of freedom - radial inside a tube stretching and squeezing a spring and pseudo-circular as it moves together with a tube in a pendulum like motion.
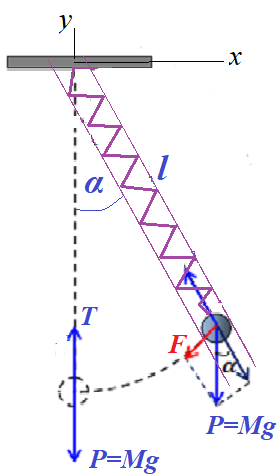 The problem of specifying the motion of an object is much more complex here because the spring tension is changing not only with an angle α(t) but also because of the movement of an object within a tube.
The problem of specifying the motion of an object is much more complex here because the spring tension is changing not only with an angle α(t) but also because of the movement of an object within a tube.
However, using the Langrangian mechanics, this problem can be analyzed with much less efforts and the corresponding differential equation can be constructed relatively easy.
As before, let's calculate the kinetic and potential energies of an object.
The object's kinetic energy can be calculated as a sum of its radial movement's kinetic energy inside the tube and kinetic energy of its pseudo-circular movement perpendicularly to the tube.
The reason is simple. The object's linear velocity vector can be represented as a sum of two perpendicular to each other vectors, one is inside the tube and another perpendicular to it.
v = v|| + v⊥
Since kinetic energy depends on a square of the linear speed, according to Pythagorean Theorem
v² = v||² + v⊥²
from which follows that
Ekin = ½M·v² =
= ½M·v||² + ½M·v⊥²
Distance of an object from the fixed point of oscillation l is variable and depends on time: l=l(t).
Therefore, v||(t)=l'(t).
Perpendicular to l component of an object speed is v⊥(t)=l(t)·α'(t).
Therefore, kinetic energy of an object is
Ekin = ½M·[l'(t)²+l(t)²·α'(t)²]
The object's potential energy can be calculated as a sum of its potential energy due to gravity and potential energy of a stretched or a squeezed spring.
If the fixed point of oscillation is at the height H above the ground, an object is at height h(t)=H−l(t)·cos(α(t)) above the ground, and potential energy of an object related to its position in the gravitational field is
Egrav = M·g·[H−l(t)·cos(α(t))]
Potential energy of a spring depends on the degree of its stretching or squeezing.
Assume, the length of a spring in a neutral state is l0. Then the length of stretching or squeezing at time t is l(t)−l0.
Therefore, potential energy of an object related to a spring is
Espr = ½k·[l(t)−l0]²
where k is a coefficient of elasticity of a spring.
Total potential energy of an object is
Epot = Egrav + Espr =
= M·g·[H−l(t)·cos(α(t))] +
+ ½k·[l(t)−l0]²
Construct Lagrangian
L(l,l',α,α') = Ekin − Epot =
= ½M·[l'(t)²+l(t)²·α'(t)²] −
− M·g·[H−l(t)·cos(α(t))] −
− ½k·[l(t)−l0]²
All which remains is to write the Euler-Lagrange equation for this Lagrangian.
The problem is, we are familiar only with the Euler-Lagrange equation for a system with one degree of freedom, like x(t). Now we have two degrees of freedom - l(t) and α(t).
Fortunately, the Euler-Lagrange equation can be specified for each degree of freedom independently, which will be proven in the next lecture.
Therefore, we can write two independent Euler-Lagrange equations (skipping (t) for brevity):
(∂/∂l)L(l,l',α,α') =
= (d/dt)(∂/∂l')L(l,l',α,α')
and
(∂/∂α)L(l,l',α,α') =
= (d/dt)(∂/∂α')L(l,l',α,α')
The first equation is
M·l·α'²+M·g·cos(α)−k·(l−l0) =
= M·l"
The second equation is
−M·g·l·sin(α) = M·l²·α"
or
−g·sin(α) = l·α"
or
−(g/l)·sin(α) = α"
which looks exactly the same as in the case above with unstretchable thread instead of a spring.
Mathematical Pendulum
Plain Pendulum
We will illustrate the application of Lagrangian mechanics by analyzing the movement of a mathematical pendulum - a problem we have already discussed in the Physics 4 Teens - Mechanics - Pendulum, Spring - Pendulum using the Newtonian approach.

We recommend reviewing the lecture mentioned above and refresh the Newtonian method of deriving the main equation of motion of the pendulum:
α"(t) = −(g/l)·sin(α(t))
which was obtained from properly determining the force F that moves a pendulum as a vector sum of the gravity force directed vertically down and the tension of an unstretchable thread that keeps an object at the free end of a thread on a constant distance from the fixed end of a thread.
The two forces involved in formation of a resulting force F, gravity P=m·g and tension of a thread T, had to be combined using the rules for addition of vectors, which required some thinking.
Let's apply the Lagrangian mechanics to this problem using an angle of a thread with a vertical α as the one and only parameter that determines a position of an object.
This way of identification of a position is more convenient than Cartesian coordinates originated at the fixed end of a thread because both of them can be easily derived from α
x = l·sin(α)
y = −l·cos(α)
The Lagrangian is the difference between kinetic and potential energies.
L(α(t),α'(t)) =
= Ekin(α'(t)) − Epot(α(t))
Kinetic energy depends on mass M and linear speed of an object along its circular trajectory v=l·α'(t)
Ekin = ½M·v² =
= ½M·l²·[α'(t)]²
Potential energy depends on a mass of an object M, its height over the ground h(t) and an acceleration of free fall g.
Epot(t) = M·g·h(t)
If the origin of our coordinates, the fixed end of a thread, is at height H over the ground,
h = H − l·cos(α)
and, therefore,
Epot(t) = M·g·[H−l·cos(α(t))]
Now we can construct the Euler-Lagrange equation
(∂/∂α)L(α(t),α'(t)) =
= (d/dt)(∂/∂α')L(α(t),α'(t))
Calculate left and right sides separately.
(∂/∂α)L(α(t),α'(t)) =
= (∂/∂α)[Ekin(α'(t)) − Epot(α(t))] =
= (∂/∂α)[−Epot(α(t))] =
= (∂/∂α)[−M·g·[H−l·cos(α(t))]] =
= −M·g·l·sin(α(t))
(d/dt)(∂/∂α')L(α(t),α'(t)) =
=(d/dt)(∂/∂α')[Ekin(α'(t))−Epot(α(t))]=
= (d/dt)(∂/∂α')Ekin(α'(t)) =
= (d/dt)(∂/∂α')½M·l²·[α'(t)]² =
= (d/dt)M·l²·α'(t) =
= M·l²·α"(t)
The Euler-Lagrange equation is
−M·g·l·sin(α(t)) = M·l²·α"(t)
or
α"(t) = −(g/l)·sin(α(t))
which is exactly as applying Newtonian mechanics.
If you don't think the Lagrangian mechanics is simpler than Newtonian for those who are familiar with Calculus of partial derivatives, consider the next example.
Spring Pendulum
A weightless spring replaces an unstretchable thread of the previous problem.
The spring and an object on its end are in a weightless frictionless tube that maintains a straight form, so an object has two degrees of freedom - radial inside a tube stretching and squeezing a spring and pseudo-circular as it moves together with a tube in a pendulum like motion.
 The problem of specifying the motion of an object is much more complex here because the spring tension is changing not only with an angle α(t) but also because of the movement of an object within a tube.
The problem of specifying the motion of an object is much more complex here because the spring tension is changing not only with an angle α(t) but also because of the movement of an object within a tube.However, using the Langrangian mechanics, this problem can be analyzed with much less efforts and the corresponding differential equation can be constructed relatively easy.
As before, let's calculate the kinetic and potential energies of an object.
The object's kinetic energy can be calculated as a sum of its radial movement's kinetic energy inside the tube and kinetic energy of its pseudo-circular movement perpendicularly to the tube.
The reason is simple. The object's linear velocity vector can be represented as a sum of two perpendicular to each other vectors, one is inside the tube and another perpendicular to it.
v = v|| + v⊥
Since kinetic energy depends on a square of the linear speed, according to Pythagorean Theorem
v² = v||² + v⊥²
from which follows that
Ekin = ½M·v² =
= ½M·v||² + ½M·v⊥²
Distance of an object from the fixed point of oscillation l is variable and depends on time: l=l(t).
Therefore, v||(t)=l'(t).
Perpendicular to l component of an object speed is v⊥(t)=l(t)·α'(t).
Therefore, kinetic energy of an object is
Ekin = ½M·[l'(t)²+l(t)²·α'(t)²]
The object's potential energy can be calculated as a sum of its potential energy due to gravity and potential energy of a stretched or a squeezed spring.
If the fixed point of oscillation is at the height H above the ground, an object is at height h(t)=H−l(t)·cos(α(t)) above the ground, and potential energy of an object related to its position in the gravitational field is
Egrav = M·g·[H−l(t)·cos(α(t))]
Potential energy of a spring depends on the degree of its stretching or squeezing.
Assume, the length of a spring in a neutral state is l0. Then the length of stretching or squeezing at time t is l(t)−l0.
Therefore, potential energy of an object related to a spring is
Espr = ½k·[l(t)−l0]²
where k is a coefficient of elasticity of a spring.
Total potential energy of an object is
Epot = Egrav + Espr =
= M·g·[H−l(t)·cos(α(t))] +
+ ½k·[l(t)−l0]²
Construct Lagrangian
L(l,l',α,α') = Ekin − Epot =
= ½M·[l'(t)²+l(t)²·α'(t)²] −
− M·g·[H−l(t)·cos(α(t))] −
− ½k·[l(t)−l0]²
All which remains is to write the Euler-Lagrange equation for this Lagrangian.
The problem is, we are familiar only with the Euler-Lagrange equation for a system with one degree of freedom, like x(t). Now we have two degrees of freedom - l(t) and α(t).
Fortunately, the Euler-Lagrange equation can be specified for each degree of freedom independently, which will be proven in the next lecture.
Therefore, we can write two independent Euler-Lagrange equations (skipping (t) for brevity):
(∂/∂l)L(l,l',α,α') =
= (d/dt)(∂/∂l')L(l,l',α,α')
and
(∂/∂α)L(l,l',α,α') =
= (d/dt)(∂/∂α')L(l,l',α,α')
The first equation is
M·l·α'²+M·g·cos(α)−k·(l−l0) =
= M·l"
The second equation is
−M·g·l·sin(α) = M·l²·α"
or
−g·sin(α) = l·α"
or
−(g/l)·sin(α) = α"
which looks exactly the same as in the case above with unstretchable thread instead of a spring.
Wednesday, August 20, 2025
Physics+ Lagrangian: UNIZOR.COM - Physics+ 4 All - Lagrangian
Notes to a video lecture on UNIZOR.COM
Lagrangian
First of all, let's stipulate that the Laws of Newton are based on experiment, they are not derived from some more fundamental theories.
Lagrangian mechanics presents a different approach to analyze the motion than Newtonian mechanics.
In many cases it presents a simpler, more universal way to describe the motion of a mechanical system than Newtonian one.
Let's start with an example where both methodologies lead to the same result.
Spring Oscillation
Consider an ideal spring with one end fixed and a point-mass attached to another end.
The oscillations will occur along the length of a spring that coincides with X-axis.
Position of a point-mass on the spring's end will be described by it X-coordinate x(t) as a function of time t with initial position at time t=0 being an origin of X-coordinate, that is x(0)=0.
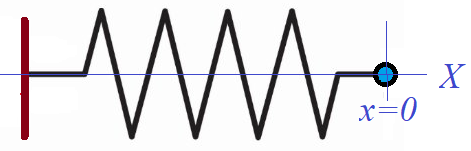
According to the Hooke's Law, the force F of a spring applied to an object attached to its end is proportional to a length x by which this spring is stretched or squeezed from its neutral position and directed always towards a neutral point x=0 of no stretching or squeezing.
F = −k·x
where k is a coefficient of elasticity that characterizes physical properties of a spring.
According to the Newton's Second Law, the acceleration a of an object is proportional to a force F applied to it
F = m·a
where m is the object's mass being a coefficient of proportionality.
A linear acceleration a(t), as a function of time, is a derivative of a linear speed v(t) by time t
a(t) = dv(t)/dt = v'(t)
A linear speed v(t) is, in turn, a derivative of a position of an object x(t) by time
v(t) = dx(t)/dt = x'(t)
Therefore, an acceleration is a second derivative of a position by time
a(t) = d²x(t)/dt² = x"(t)
Equating the value of force by Hooke's Law to that of Newton's Second Law, we get a differential equation that defines a motion of the object
−k·x(t) = m·a(t)
or, equivalently,
−k·x(t) = m·x"(t)
Solution to this differential equation of the second order is a trajectory of our object.
Let's approach the same problem from another side.
An object attached to a spring's end that has mass m and linear speed v has kinetic energy that is equal to
Ekin = ½m·v²
Since speed v(t), as a function of time t is just a derivative of a position x(t) by time, we can express kinetic energy in terms of position, as in the case of potential energy above
Ekin = ½m·[x'(t)]²
NOTICE:
Ekin depends explicitly only on speed x'(t) and
d/dt[∂(Ekin)/∂x'] =
= d/dt[m·x'] = mx"(t) = F
A stretched or a squeezed spring has potential energy equal to the amount of work needed to stretch or squeeze it against the force of its elasticity (you can refer to a lecture Physics 4 Teens - Energy - Potential Energy - Spring on UNIZOR.COM).
Thus, a potential energy of a spring squeezed or stretched by the length x(t), as a function of time t, equals to
Epot = ½k·[x(t)]²
where k is the same coefficient of elasticity as above that characterizes the physical properties of a spring.
NOTICE:
Epot depends explicitly only on position x(t) and
∂(−Epot)/∂x = −k·x(t) = F
Based on two NOTICEs above, it is IMPORTANT to see that
∂(−Epot)/∂x =
= d/dt[∂(Ekin)/∂x'] = F
Φ[f(x)] = ∫[a,b] F[x,f(x),f '(x)]dx
where F[...] is some known smooth real function of three arguments - real variable x, real value of function f(x) and real value of derivative f '(x).
This Euler-Lagrange differential equation looks like this:
(∂/∂f)F [x,f0(x),f '0(x)] =
= (d/dx)(∂/∂f ')F [x,f0(x),f '0(x)]
Let's change more abstract symbols x and f(x) to those applicable to our task.
The argument will be time t instead of abstract x. The function will be a position x(t) instead of abstract f0(x).
Now the Euler-Lagrange equation looks like
(∂/∂x)F [t,x(t),x'(t)] =
= (d/dt)(∂/∂x')F [t,x(t),x'(t)]
Compare this to the equation above that equates partial derivative from Ekin−Epot by x with its partial derivative by x'.
At any moment it has certain kinetic and potential energy, so we can constract a Lagrangian
L(t) = Ekin(x'(t)) − Epot(x(t))
Consider an integral of this Lagrangian by time
S = ∫[t1,t2]L(t)·dt
This integral is call action.
The trajectory that minimizes or maximizes this action is a solution to an Euler-Lagrange equation
(∂/∂x)L[x(t),x'(t)] =
= (d/dt)(∂/∂x')L[t,x(t),x'(t)]
which has the same solution as Newtonian F=m·a.
Therefore, the trajectory obtained using a Lagrangian approach is the same the one from Newtonian mechanics. BUT IN SOME CASES IT MIGHT BE MUCH MORE CONVENIENT.
The equivalence of a differential equation obtained from the Newton's Second Law and the Euler-Lagrange equation is not just a coincidence peculiar for springs.
In general, kinetic energy always depends on mass and speed
Ekin = ½m·v²
In general, derivative of Ekin by speed v is a momentum of motion p
p = m·v = ∂/∂v(Ekin) =
= ∂/∂v(½mv²)
In general, derivative of momentum p by time t is the force F
dp/dt = d(m·v)/dt = m·a = F
In general, potential energy is, actually, an amount of work W.
Since dW=F·dx, its derivative by x is the force, and a derivative of potential energy by coordinates gives the force as well.
So, the Newton's Second Law and Euler-Lagrange equation are equivalent. Why do we need both?
Practical mechanical problems are rarely as simple as we are taught at high school.
It appears that the more complicated problems with more than one object involved are easier to solve using Lagrangian L=Ekin−Epot than to deal with complicated forces and their interaction constructing the equations of F=m·a type.
The next lectures will be dedicated to a few important physical problems and their solutions using Euler-Lagrange equation.
Lagrangian
First of all, let's stipulate that the Laws of Newton are based on experiment, they are not derived from some more fundamental theories.
Lagrangian mechanics presents a different approach to analyze the motion than Newtonian mechanics.
In many cases it presents a simpler, more universal way to describe the motion of a mechanical system than Newtonian one.
Let's start with an example where both methodologies lead to the same result.
Spring Oscillation
Consider an ideal spring with one end fixed and a point-mass attached to another end.
The oscillations will occur along the length of a spring that coincides with X-axis.
Position of a point-mass on the spring's end will be described by it X-coordinate x(t) as a function of time t with initial position at time t=0 being an origin of X-coordinate, that is x(0)=0.

According to the Hooke's Law, the force F of a spring applied to an object attached to its end is proportional to a length x by which this spring is stretched or squeezed from its neutral position and directed always towards a neutral point x=0 of no stretching or squeezing.
F = −k·x
where k is a coefficient of elasticity that characterizes physical properties of a spring.
According to the Newton's Second Law, the acceleration a of an object is proportional to a force F applied to it
F = m·a
where m is the object's mass being a coefficient of proportionality.
A linear acceleration a(t), as a function of time, is a derivative of a linear speed v(t) by time t
a(t) = dv(t)/dt = v'(t)
A linear speed v(t) is, in turn, a derivative of a position of an object x(t) by time
v(t) = dx(t)/dt = x'(t)
Therefore, an acceleration is a second derivative of a position by time
a(t) = d²x(t)/dt² = x"(t)
Equating the value of force by Hooke's Law to that of Newton's Second Law, we get a differential equation that defines a motion of the object
−k·x(t) = m·a(t)
or, equivalently,
−k·x(t) = m·x"(t)
Solution to this differential equation of the second order is a trajectory of our object.
Let's approach the same problem from another side.
An object attached to a spring's end that has mass m and linear speed v has kinetic energy that is equal to
Ekin = ½m·v²
Since speed v(t), as a function of time t is just a derivative of a position x(t) by time, we can express kinetic energy in terms of position, as in the case of potential energy above
Ekin = ½m·[x'(t)]²
NOTICE:
Ekin depends explicitly only on speed x'(t) and
d/dt[∂(Ekin)/∂x'] =
= d/dt[m·x'] = mx"(t) = F
A stretched or a squeezed spring has potential energy equal to the amount of work needed to stretch or squeeze it against the force of its elasticity (you can refer to a lecture Physics 4 Teens - Energy - Potential Energy - Spring on UNIZOR.COM).
Thus, a potential energy of a spring squeezed or stretched by the length x(t), as a function of time t, equals to
Epot = ½k·[x(t)]²
where k is the same coefficient of elasticity as above that characterizes the physical properties of a spring.
NOTICE:
Epot depends explicitly only on position x(t) and
∂(−Epot)/∂x = −k·x(t) = F
Based on two NOTICEs above, it is IMPORTANT to see that
∂(−Epot)/∂x =
= d/dt[∂(Ekin)/∂x'] = F
Since Epot depends explicitly only on position x(t), not on speed x'(t), and Ekin depends explicitly only on speed x'(t), not on position x(t),
∂(Ekin−Epot)/∂x =
= ∂(−Epot)/∂x =
= d/dt[∂(Ekin)/∂x'] =
= d/dt[∂(Ekin−Epot)/∂x']
Φ[f(x)] = ∫[a,b] F[x,f(x),f '(x)]dx
where F[...] is some known smooth real function of three arguments - real variable x, real value of function f(x) and real value of derivative f '(x).
This Euler-Lagrange differential equation looks like this:
(∂/∂f)F [x,f0(x),f '0(x)] =
= (d/dx)(∂/∂f ')F [x,f0(x),f '0(x)]
Let's change more abstract symbols x and f(x) to those applicable to our task.
The argument will be time t instead of abstract x. The function will be a position x(t) instead of abstract f0(x).
Now the Euler-Lagrange equation looks like
(∂/∂x)F [t,x(t),x'(t)] =
= (d/dt)(∂/∂x')F [t,x(t),x'(t)]
Compare this to the equation above that equates partial derivative from Ekin−Epot by x with its partial derivative by x'.
Obviously, L=Ekin−Epot satisfies the Euler-Lagrange equation
(∂/∂x)L[t,x(t),x'(t)] =
= (d/dt)(∂/∂x')L[t,x(t),x'(t)]
which in this case is exactly the same as the equation obtained from the Newton's Second Law
−k·x(t) = m·x"(t)
Expression
L[x(t),x'(t)]=Ekin(x')−Epot(x)
is called Lagrangian.
At any moment it has certain kinetic and potential energy, so we can constract a Lagrangian
L(t) = Ekin(x'(t)) − Epot(x(t))
Consider an integral of this Lagrangian by time
S = ∫[t1,t2]L(t)·dt
This integral is call action.
The trajectory that minimizes or maximizes this action is a solution to an Euler-Lagrange equation
(∂/∂x)L[x(t),x'(t)] =
= (d/dt)(∂/∂x')L[t,x(t),x'(t)]
which has the same solution as Newtonian F=m·a.
Therefore, the trajectory obtained using a Lagrangian approach is the same the one from Newtonian mechanics. BUT IN SOME CASES IT MIGHT BE MUCH MORE CONVENIENT.
The equivalence of a differential equation obtained from the Newton's Second Law and the Euler-Lagrange equation is not just a coincidence peculiar for springs.
In general, kinetic energy always depends on mass and speed
Ekin = ½m·v²
In general, derivative of Ekin by speed v is a momentum of motion p
p = m·v = ∂/∂v(Ekin) =
= ∂/∂v(½mv²)
In general, derivative of momentum p by time t is the force F
dp/dt = d(m·v)/dt = m·a = F
In general, potential energy is, actually, an amount of work W.
Since dW=F·dx, its derivative by x is the force, and a derivative of potential energy by coordinates gives the force as well.
So, the Newton's Second Law and Euler-Lagrange equation are equivalent. Why do we need both?
Practical mechanical problems are rarely as simple as we are taught at high school.
It appears that the more complicated problems with more than one object involved are easier to solve using Lagrangian L=Ekin−Epot than to deal with complicated forces and their interaction constructing the equations of F=m·a type.
The next lectures will be dedicated to a few important physical problems and their solutions using Euler-Lagrange equation.
Monday, August 18, 2025
Physics+ Brachistochrone: UNIZOR.COM - Physics+ 4 All - Variations
Notes to a video lecture on UNIZOR.COM
Brachistochrone
The approach to choose a path along which any system progresses (light propagates, planet moves around the Sun etc.) based on minimizing some numeric function defined for each path appears to be very valuable in Physics, and it helps to solve certain tasks faster and more efficiently than using only the classic Newton's Laws.
Before generalizing this idea, let's consider a specific problem suggested by Johann Bernoulli in 1696.
It's called the Brachistochrone problem (from Greek 'brachistos' + 'chronus' = 'short' + 'time') and is formulated as follows.
Consider two points A and B in the uniform gravitational field (like near the surface of the Earth) with force of gravity directed vertically down. These points are positioned on different heights and not on the same vertical.
A small object should slide from the top point A(a,A) to the lower point B(b,B) along some frictionless supporting track.
We use a standard Cartesian reference frame withY-coordinates increasing upwards, and X-coordinates increasing from left to right on a picture above.
The vector of gravity force is directed down along Y-axis.
Therefore,Y-coordinate A is greater then B, and X-coordinate a is less than b.
The supporting track can go straight from A to B or take some curved form.
The straight brown line of descend on a picture above is shorter, but the curved blue or purple lines, while longer, allow for an object to gain speed faster and the resulting time of descend might still be shorter than for a straight line.
The problem is to determine the shape of a supporting track to minimize the time of sliding.
Mathematically speaking, we have to consider all smooth functions f(x) on a segment [a,b] that satisfy the conditions:
f(a) = A and f(b) = B
Then, out of all these functions, we have to find such that represents the curve of fastest descend from A(a,A) to B(b,B).
This simply formulated problem is far from having a simple solution.
Best mathematicians of 17th century worked on it and solved using different methodologies.
Let's solve it using the apparatus developed for finding a minimum of a functional - the Euler-Lagrange equation. This methodology was discussed in the previous lectures of this course.
We have to express the time T of moving from point A to point B as a functional of a trajectory represented by function f(x):
T = Φ[f(x)]
and find a function y=f0(x) that minimizes this functional.
Hopefully, our functional will look like
Φ[f(x)] = ∫[a,b] F[x,f(x),f '(x)]dx
where F[...] is some known smooth real function of three arguments - real variable x, real value of function f(x) and real value of derivative f '(x)
and we will be able to apply Euler-Lagrange equation to find y=f0(x) as its solution.

The picture above illustrates a trajectory of a movement of an object in a uniform gravitational field along a supporting curved track described by a function y=f(x).
The object's weight (the force of gravity vector) is P=m·g, where m is its mass and g is an acceleration of a free falling in the gravitational field.
Besides the gravitational force, a reaction of a supporting curved track vector of force R acts on this object - the force always directed perpendicularly to a tangential line to a curve.
Both the force of gravity P and the reaction force of a curved track R result in the force vector F moving an object along a trajectory and directed along a tangential line to a curved track.
Consider a segment of a trajectory from x to x+dx, where dx is an infinitesimal increment of argument x.
This segment has a length ds and its value satisfies the Pythagorean Theorem
(ds)² = (dx)² + (dy)²
where dy=d(f(x))=f '(x)·dx
so (ds)²=[1+(f '(x))²]·(dx)²
and ds=√1+(f '(x))²·dx
Assume, at point x the linear sliding speed of an object along its trajectory is v(x).
Then the time an object spends passing a segment ds equals to
ds/v(x) = √1+(f '(x))²·dx / v(x)
To find speed of an object v(x), recall the Conservation of Energy Law.
Potential energy of an object depends on its mass and the height over some zero level.
Assume, the zero level of potential energy is at y=0.
Then the initial potential energy Ua of our object at the beginning of its motion is
Ua = m·g·A
where m is an object's mass,
g is an acceleration of free falling and
A is its initial Y-coordinate.
Its kinetic energy Ka at the beginning is zero because its speed along a trajectory is zero at that point.
Then the total initial mechanical energy of an object (potential + kinetic) is
Ea = m·g·A
When our object moved along a curve from its initial position at (a,A) to position (x,f(x)), its potential energy diminished and kinetic energy grew by the same amount because of the Energy Conservation Law.
New potential energy equals to
Ux = m·g·f(x)
New kinetic energy equals to
Kx =m·v²(x)/2.
The decrease in potential energy Ua−Ux should be compensated by an increase in kinetic energy Kx.
From the Energy Conservation Law the total energy should remain the same Ea = Ex
which leads us to an equation
m·g·[A−f(x)] = m·v²(x)/2
Therefore,
v(x) = √2g·[A−f(x)]
Now the time an object spends passing a segment ds equals to
Integrating this by x from a to b gives a total time of moving along a trajectory - the functional we need to minimize
Φ[f(x)] = ∫[a,b] dT(x)
or
At this point we can drop 2g from the denominator, as this does not change the function-argument f0(x) that minimizes functional Φ[f(x)].
So, our task is to minimize a functional
Recall from the previous lecture that for a given functional
Φ[f(x)] = ∫[a,b] F[x,f(x),f '(x)]dx
the function f0(x) that minimizes or maximizes it should satisfy the Euler-Lagrange differential equation
(∂/∂f)F [x,f0(x),f '0(x)] −
− (d/dx)(∂/∂f ')F [x,f0(x),f '0(x)] = 0
Let's construct this equation for our case.
To shorten formulas, let's temporarily use
h(x) instead of f '(x) and
omit (x) from both f(x) and h(x).
Using this substitution, our functional looks like
From this follows that an expression under an integral is
In terms of these functions, the Euler-Lagrange equation looks like
(∂/∂f)F [x,f,h] =
= (d/dx)(∂/∂h)F [x,f,h]
Let's calculate each term separately.
Left side of an equation is
(∂/∂f)F [x,f,h] =
= √1+h²·(∂/∂f)(A−f)−½ =
= √1+h²·(−½)·(A−f)−3/2·(−1) =
Right side of an equation is
(d/dx)(∂/∂h)F [x,f,h] =
Note that we've agreed to substitute h(x) for f '(x) in the numerator of the last term.
Equating left and right sides of the Euler-Lagrange equation, multiplying both sides by 2√(1+h²)³ ·√(A−f)³ and opening the parenthesis leads to a simpler equation
1 + h² − 2h'·(A−f) = 0
Returning back to original symbols, replace f with f(x) and h with f '(x) getting a second order differential equation for function y=f(x)
1+[f '(x)]²−2f "(x)·[A−f(x)] = 0
or, equivalently,
1+y'²−2y"·(A−y) = 0
The solution y=f0(x) to this second order differential equation is the function that minimizes the functional Φ[f(x)].
A not so obvious transformation can reduce this second order differential equation to the first order one.
Integration is easy if a subject of an integration is a derivative of some function
∫ s'(x)·dx = s(x) + C
where C is some constant.
The left side of the equation above is not a derivative of any function, but let's see what happens if we multiply it by −y'.
−y'·[1+y'²−2y"·(A−y)] =
= −y'·(1+y'²)+2y'·y"·(A−y)
Notice that we can substitute −y' with (A−y)' and 2y'·y" with (1+y'²)' to get
(A−y)'·(1+y'²) +
+ (A−y)·(1+y'²)'
which is a derivative of a product of (A−y) by (1+y'²).
Therefore, if y=f0(x) is a solution to Euler-Lagrange equation
1+y'²−2y"·(A−y) = 0,
it's also a solution to the equation
−y'·[1+y'²−2y"·(A−y)] =
[(A−y)·(1+y'²)]' = 0
or,
{[A−f0(x)]·[1+f0'(x)²]}' = 0
Integrating this, we get the first order differential equation
[A−f0(x)]·[1+f0'(x)²] = C
or, in a shorter notation,
(A−y)·(1+y'²) = C
where C is some constant.
We can solve this differential equation for function y=f0(x) as follows.
Let's resolve this differential equation for y':
From physical considerations, our function must decrease with increase of x. Therefore, it's derivative must be negative, and we will choose a minus sign in all transformations below.
This differential equation can be transformed to integrate separately by x and y:
We can integrate now both sides separately.
Without getting into the details of integration, we can just write the result of the integration by y of the left size.
− √(A−y)·(C−A+y) + D
where C and D are some constants.
Integration of dx produces x+E, where E is yet another constant, but we can combine it into constant D that appears in integration by dy.
Therefore, our function y=f0(x) that minimizes the object's time of sliding down can be expressed as
− √(A−y)·(C−A+y) + D
where C and D are some constants.
It's not really expressed as y being a function of x, just the opposite way, but it should not stop us to explore this curve.
As we see, the function depends on two constants C and D. At the same time we have two initial conditions:
f0(a) = A and
f0(b) = B
Substituting x=a, y=A into an equation above will produce on equation for C and D.
Substituting x=b, y=B into this equation will produce another equation for C and D.
These two equations determine the values of C and D needed to specify the full solution to a problem.
As an example, we used points A(1,5) and B(4,1) and calculated approximate values
C=5.8 and D=−10.1.
Here is the graph that, in particular, crosses points A(1,5) and B(4,1).
At the end of this discussion about brachistochrone it's appropriate to mention that the curve we have found as a solution to the Euler-Lagrange equation is a cycloid - a trajectory of a point on a circle that is rolling along a straight line.
We have not discussed this because our main purpose was just to show how to use the Euler-Lagrange equation to find an extremum of a functional.
Brachistochrone
The approach to choose a path along which any system progresses (light propagates, planet moves around the Sun etc.) based on minimizing some numeric function defined for each path appears to be very valuable in Physics, and it helps to solve certain tasks faster and more efficiently than using only the classic Newton's Laws.
Before generalizing this idea, let's consider a specific problem suggested by Johann Bernoulli in 1696.
It's called the Brachistochrone problem (from Greek 'brachistos' + 'chronus' = 'short' + 'time') and is formulated as follows.
Consider two points A and B in the uniform gravitational field (like near the surface of the Earth) with force of gravity directed vertically down. These points are positioned on different heights and not on the same vertical.

A small object should slide from the top point A(a,A) to the lower point B(b,B) along some frictionless supporting track.
We use a standard Cartesian reference frame with
The vector of gravity force is directed down along Y-axis.
Therefore,
The supporting track can go straight from A to B or take some curved form.
The straight brown line of descend on a picture above is shorter, but the curved blue or purple lines, while longer, allow for an object to gain speed faster and the resulting time of descend might still be shorter than for a straight line.
The problem is to determine the shape of a supporting track to minimize the time of sliding.
Mathematically speaking, we have to consider all smooth functions f(x) on a segment [a,b] that satisfy the conditions:
f(a) = A and f(b) = B
Then, out of all these functions, we have to find such that represents the curve of fastest descend from A(a,A) to B(b,B).
This simply formulated problem is far from having a simple solution.
Best mathematicians of 17th century worked on it and solved using different methodologies.
Let's solve it using the apparatus developed for finding a minimum of a functional - the Euler-Lagrange equation. This methodology was discussed in the previous lectures of this course.
We have to express the time T of moving from point A to point B as a functional of a trajectory represented by function f(x):
T = Φ[f(x)]
and find a function y=f0(x) that minimizes this functional.
Hopefully, our functional will look like
Φ[f(x)] = ∫[a,b] F[x,f(x),f '(x)]dx
where F[...] is some known smooth real function of three arguments - real variable x, real value of function f(x) and real value of derivative f '(x)
and we will be able to apply Euler-Lagrange equation to find y=f0(x) as its solution.

The picture above illustrates a trajectory of a movement of an object in a uniform gravitational field along a supporting curved track described by a function y=f(x).
The object's weight (the force of gravity vector) is P=m·g, where m is its mass and g is an acceleration of a free falling in the gravitational field.
Besides the gravitational force, a reaction of a supporting curved track vector of force R acts on this object - the force always directed perpendicularly to a tangential line to a curve.
Both the force of gravity P and the reaction force of a curved track R result in the force vector F moving an object along a trajectory and directed along a tangential line to a curved track.
Consider a segment of a trajectory from x to x+dx, where dx is an infinitesimal increment of argument x.
This segment has a length ds and its value satisfies the Pythagorean Theorem
(ds)² = (dx)² + (dy)²
where dy=d(f(x))=f '(x)·dx
so (ds)²=[1+(f '(x))²]·(dx)²
and ds=√1+(f '(x))²·dx
Assume, at point x the linear sliding speed of an object along its trajectory is v(x).
Then the time an object spends passing a segment ds equals to
ds/v(x) = √1+(f '(x))²·dx / v(x)
To find speed of an object v(x), recall the Conservation of Energy Law.
Potential energy of an object depends on its mass and the height over some zero level.
Assume, the zero level of potential energy is at y=0.
Then the initial potential energy Ua of our object at the beginning of its motion is
Ua = m·g·A
where m is an object's mass,
g is an acceleration of free falling and
A is its initial Y-coordinate.
Its kinetic energy Ka at the beginning is zero because its speed along a trajectory is zero at that point.
Then the total initial mechanical energy of an object (potential + kinetic) is
Ea = m·g·A
When our object moved along a curve from its initial position at (a,A) to position (x,f(x)), its potential energy diminished and kinetic energy grew by the same amount because of the Energy Conservation Law.
New potential energy equals to
Ux = m·g·f(x)
New kinetic energy equals to
Kx =m·v²(x)/2.
The decrease in potential energy Ua−Ux should be compensated by an increase in kinetic energy Kx.
From the Energy Conservation Law the total energy should remain the same Ea = Ex
which leads us to an equation
m·g·[A−f(x)] = m·v²(x)/2
Therefore,
v(x) = √2g·[A−f(x)]
Now the time an object spends passing a segment ds equals to
| dT(x) = |
|
dx |
Integrating this by x from a to b gives a total time of moving along a trajectory - the functional we need to minimize
Φ[f(x)] = ∫[a,b] dT(x)
or
| Φ[f(x)]=∫[a,b] |
|
dx |
So, our task is to minimize a functional
| Φ[f(x)]=∫[a,b] |
|
dx |
Recall from the previous lecture that for a given functional
Φ[f(x)] = ∫[a,b] F[x,f(x),f '(x)]dx
the function f0(x) that minimizes or maximizes it should satisfy the Euler-Lagrange differential equation
(∂/∂f)F [x,f0(x),f '0(x)] −
− (d/dx)(∂/∂f ')F [x,f0(x),f '0(x)] = 0
Let's construct this equation for our case.
To shorten formulas, let's temporarily use
h(x) instead of f '(x) and
omit (x) from both f(x) and h(x).
Using this substitution, our functional looks like
| Φ[f(x)]=∫[a,b] |
|
dx |
From this follows that an expression under an integral is
| F[x,f,h]= |
|
(∂/∂f)F [x,f,h] =
= (d/dx)(∂/∂h)F [x,f,h]
Let's calculate each term separately.
Left side of an equation is
(∂/∂f)F [x,f,h] =
| = (∂/∂f) |
|
= |
= √1+h²·(−½)·(A−f)−3/2·(−1) =
| = |
|
Right side of an equation is
(d/dx)(∂/∂h)F [x,f,h] =
| = (d/dx)(∂/∂h) |
|
= |
| = (d/dx) |
|
= |
| = |
|
− |
| − |
|
+ |
| + |
|
Equating left and right sides of the Euler-Lagrange equation, multiplying both sides by 2√(1+h²)³ ·√(A−f)³ and opening the parenthesis leads to a simpler equation
1 + h² − 2h'·(A−f) = 0
Returning back to original symbols, replace f with f(x) and h with f '(x) getting a second order differential equation for function y=f(x)
1+[f '(x)]²−2f "(x)·[A−f(x)] = 0
or, equivalently,
1+y'²−2y"·(A−y) = 0
The solution y=f0(x) to this second order differential equation is the function that minimizes the functional Φ[f(x)].
A not so obvious transformation can reduce this second order differential equation to the first order one.
Integration is easy if a subject of an integration is a derivative of some function
∫ s'(x)·dx = s(x) + C
where C is some constant.
The left side of the equation above is not a derivative of any function, but let's see what happens if we multiply it by −y'.
−y'·[1+y'²−2y"·(A−y)] =
= −y'·(1+y'²)+2y'·y"·(A−y)
Notice that we can substitute −y' with (A−y)' and 2y'·y" with (1+y'²)' to get
(A−y)'·(1+y'²) +
+ (A−y)·(1+y'²)'
which is a derivative of a product of (A−y) by (1+y'²).
Therefore, if y=f0(x) is a solution to Euler-Lagrange equation
1+y'²−2y"·(A−y) = 0,
it's also a solution to the equation
−y'·[1+y'²−2y"·(A−y)] =
[(A−y)·(1+y'²)]' = 0
or,
{[A−f0(x)]·[1+f0'(x)²]}' = 0
Integrating this, we get the first order differential equation
[A−f0(x)]·[1+f0'(x)²] = C
or, in a shorter notation,
(A−y)·(1+y'²) = C
where C is some constant.
We can solve this differential equation for function y=f0(x) as follows.
Let's resolve this differential equation for y':
| dy/dx = ±√ |
|
This differential equation can be transformed to integrate separately by x and y:
| −√ |
|
·dy = dx |
Without getting into the details of integration, we can just write the result of the integration by y of the left size.
| − ∫√ |
|
·dy = |
| = − C·arctan√ |
|
− |
where C and D are some constants.
Integration of dx produces x+E, where E is yet another constant, but we can combine it into constant D that appears in integration by dy.
Therefore, our function y=f0(x) that minimizes the object's time of sliding down can be expressed as
| x = −C·arctan√ |
|
where C and D are some constants.
It's not really expressed as y being a function of x, just the opposite way, but it should not stop us to explore this curve.
As we see, the function depends on two constants C and D. At the same time we have two initial conditions:
f0(a) = A and
f0(b) = B
Substituting x=a, y=A into an equation above will produce on equation for C and D.
Substituting x=b, y=B into this equation will produce another equation for C and D.
These two equations determine the values of C and D needed to specify the full solution to a problem.
As an example, we used points A(1,5) and B(4,1) and calculated approximate values
C=5.8 and D=−10.1.
Here is the graph that, in particular, crosses points A(1,5) and B(4,1).

At the end of this discussion about brachistochrone it's appropriate to mention that the curve we have found as a solution to the Euler-Lagrange equation is a cycloid - a trajectory of a point on a circle that is rolling along a straight line.
We have not discussed this because our main purpose was just to show how to use the Euler-Lagrange equation to find an extremum of a functional.
Subscribe to:
Comments (Atom)

