Unizor - Physics4Teens - Mechanics - Dynamics - Friction - Problems 1

Notes to a video lecture on http://www.unizor.com



Friction Problems 1



Problem A



There is an object of mass m on an inclined plane that makes angle φ with horizon.

To move this object up on this inclined plane with constant speed you need to apply a force F_up directed uphill.

The coefficient of friction is unknown.

Let's assume that, left by itself, the object would slide down the
inclined plane under its own weight. The free fall acceleration is g, so the weight of an object of mass m is m·g.

What is the acceleration a of an object when it moves downhill under its own weight?



Hint

F_up = m·g·sin(φ)+μ·m·g·cos(φ)

a = g·sin(φ)−μ·g·cos(φ)



Answer:

a = 2·g·sin(φ) − F_up/m





Problem B



An object is lying on a horizontal platform that moves with acceleration a=10 m/sec².

The coefficient of kinetic friction between an object and a surface of a platform is μ=0.3, while coefficient of static friction is μ_s=0.4.

The free fall acceleration is g=9.8m/sec², so the weight of an object of mass m is m·g, but mass m is unknown.

(a) How the object will behave?

(b) Why was coefficient of static friction μ_s given?

(c) What is the acceleration of the object relative to the ground and relative to the platform?



Answer:

(a) The object will slide back along the platform's surface, but forward relative to the ground.

(b) If the coefficient of static friction is too high, the object will
not change its position relatively to a platform, and the next question
would make no sense.

(c) Relative to the ground acceleration is a₀=g·μ=2.94m/sec².

Relative to the platform acceleration is a₁=a₀−a=−7.06m/sec²

Unizor - Physics4Teens - Mechanics - Dynamics - Superposition of Forces ...

Notes to a video lecture on http://www.unizor.com



Motion on Inclined Plane



Problem A



Consider a slope fixed on the ground that makes an angle φ
with horizon. Let's analyze the motion of an object, as it slides down a
slope under its own weight. Our task is to determine its acceleration
along the slope.



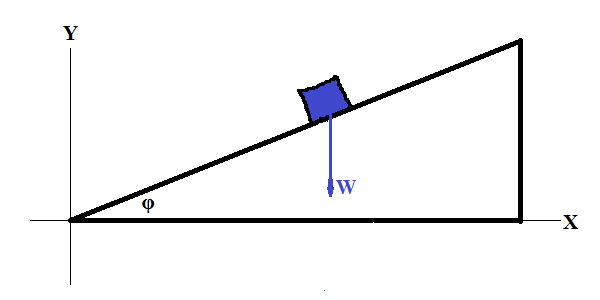
First of all, we have to choose a reference frame - a system of coordinates suitable for this problem.

The main force acting on this object is its weight W - a vector of gravity
directed vertically down to the ground. That prompts us to choose a
frame of reference with horizontal X-axis and vertical Y-axis. So, the
vector of weight has non-zero Y-component and zero X-component: W = {0,W}, where W is a magnitude of vector of weight W. However, this obvious choice is not the best in a case like this.



There are usually numerous forces involved in an experiment and only few
objects. In this case there is only one object. So, instead of catering
to one particular force, like weight, it's better to simplify the motion of a single object.

Much more convenient frame of reference would be the one, where our object in motion has only one non-zero coordinate.



Recall that there must be another force acting on an object - reaction force of the slope, that prevents an object to go vertically down to the ground through a slope and forces it, in cooperation with gravity force, to slide along a slope. This reaction force R
is always perpendicular to the surface, where an object is on (in this
case, perpendicular to a slope), and its magnitude is such that the resultant of the weight W and reaction R is directed along a slope.



Consider a frame of reference with X-axis going along the slope, where the object slides down and Y-axis perpendicular to it.



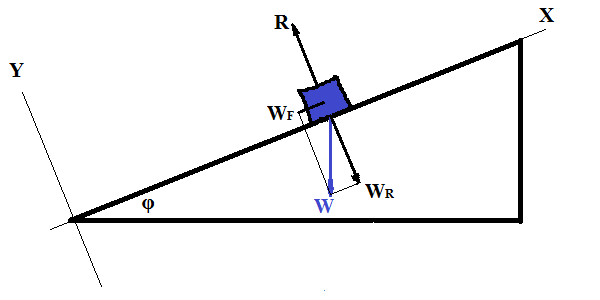
Granted, the weight now has both coordinates non-zero:

(a) perpendicular to a surface of a slope and (on the picture above) directed along negative Y-coordinates vector W_R with magnitude W_R=W·cos(φ), that causes reaction force R, that is equal in magnitude and opposite in direction to W_R, and

(b) parallel to a slope, directed (on the picture) towards negative X-coordinate, vector W_F with magnitude W_F=W·sin(φ), that is the cause of motion of our object down a slope.



As it is pictured, both components of weight are negative since they are
directed towards negative direction of the X- and Y-axes:

W = {−W·sin(φ),−W·cos(φ)}

Force R , as opposite and equal in magnitude to W_R, is

R = {0,W·cos(φ)}.



The resultant of three vectors W_R, W_F and R is W_F, directed down a slope, equaled in magnitude to W·sin(φ).



Therefore, an object of mass M will slide down a slope with acceleration equaled in magnitude to

a = W_F/M = W·cos(φ)/M

Since weight and mass of an object are related as W=M·g, where g is a known acceleration of free falling (9.8 m/sec² on the Earth ground), the resulting acceleration equals in magnitude to

a = M·g·sin(φ)/M = g·sin(φ)

In vector form in the chosen reference frame:

a = {−g·sin(φ), 0}





Problem B



Consider an object A of mass m, sliding without friction
on a slope of slide B, which itself lies on a horizontal surface and can
slide on it without friction. An angle of a slope of slide B is φ with horizon, its mass is M.

Our task is to determine acceleration a of slide B.

Let's analyze the motion of object A on a slope and the motion of a
slide B, as it moves horizontally, as a result of the weight of object A
on it.





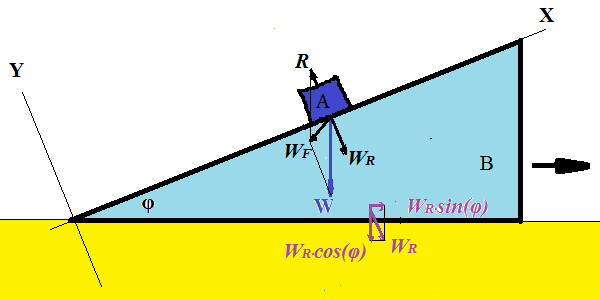
As object A presses down with its weight, it slides downhill along a
slope of a slide B. At the same time slide B moves to the right (on the
picture above).

The horizontal component of the pressure W_R of
an object A on slide B perpendicularly to its slope is the cause of the
motion of a slide B. However, this pressure is not the same as in the
problem A above. It will be less. Its opposite reaction force R, that is equal in magnitude to W_R, but acting on the object A, will also be less than in the problem A above.

The resultant of weight W and reaction force R is force W_F that is not parallel to a slope, but tilted downwards.

So, the combination of object A sliding downhill on a slope and slide B
movement to the right produces the resultant move of object A that is
not parallel to a slope, neither it is directed vertically down, but
will be somewhere in-between.



Let's consider the same reference frame as in the problem A above. Now
both object A and slide B, as they move, have both X- and Y-components
not equal to zero.



Consider only Y-coordinate of the A object now and Y-components of forces acting on it.

In the direction of Y-axis the force W_F = W + R, acting against object A, has value

W_Fy = W_y + R_y = R − W·cos(φ)



This force R − W·cos(φ), according to the Newton's Second Law, should be equal to object A's mass m, multiplied by a Y-component of its acceleration, which so far is unknown.



Let a be an acceleration of slide B in the direction of
its horizontal movement. Since displacement of object A in the direction
of the Y-axis (perpendicularly to a slope) equals to horizontal
displacement of a slide B multiplied by sin(φ), the
acceleration of slide B in the horizontal direction and acceleration of
the object A in a direction perpendicular to a slope, maintain the same
factor.

Therefore, the acceleration of object A perpendicularly to a slope of slide B equals to a·sin(φ), where a is the acceleration of the slide B that we have to determine in this problem.



The Newton's Second Law for object A in the direction of the Y-axis (perpendicular to a slope of slide B) is

R − W·cos(φ) = −m·a·sin(φ)

(minus on the right because the acceleration of object A relative to Y-axis is negative).

This equation is the first in a system of two equations that include two unknowns R and a.



On the other hand, a horizontal component of vector −R is the cause of horizontal acceleration a of slide B that has mass M.

Therefore,

R·sin(φ) = M·a

This is the second equation in a system of two equations that include two unknowns R and a.



Solving this system as follows.

From the second equation:

R = M·a/sin(φ)

Substitute it in the first equation:

M·a/sin(φ) − W·cos(φ) =

= −a·m·sin(φ)



The solution for horizontal acceleration of slide B is

a = W·cos(φ) /

/ [m·sin(φ) + M/sin(φ)] =

= W·sin(φ)·cos(φ) /

/ [m·sin²(φ)+M]



So, our final result for an acceleration a of slide B, as it moves horizontally, is
W·sin(φ)·cos(φ)/[m·sin²(φ)+M]

Unizor - Physics4Teens - Mechanics - Dynamics - Friction

Notes to a video lecture on http://www.unizor.com



Friction



What's good and bad about friction?



Friction prevents us to easily move furniture around. We can buy special
devices to make it easier, but friction is definitely prevents to move
furniture easily.

Friction is the reason why parts in many machines wear out and need replacement.

Friction between the air and a spaceship, when it enters the atmosphere,
causes tremendous heating of the spaceship's body and requires special
layer of heat-resistant material to cover the spaceship.

Friction prevents a rollerblader to roll indefinitely along the smooth straight road.

In a word, friction is bad.



But is it really?..



Friction is needed to walk on a road, to drive a car, to wear clothes,
to have furniture in place where we want it, to have plates on a table
in a steady position without slipping over the edge, to fork a piece of
meat, to hold a glass of water in a hand.

Enough! As we see, we cannot live without friction, but sometimes would like to reduce it.



So, what is friction?

Here is what causes friction:



On a micro level the surfaces of two objects touching each other are not
perfect. Each little bump of one is catching a little bump of another,
thus preventing smooth gliding of one surface over another.

As was mentioned above, there are good and bad sides of this story, but
it is what it is. We have to use this friction, when needed, and reduce,
when desired.



Static Friction



Static friction is the friction between an object at rest and surface it is positioned on.

A chair stands at a fixed place on a floor, even if the floor is slightly tilted, because static friction holds it in place.

Micro-bumps on the floor are caught in-between micro-bumps on the chair's legs and fix the chair's position on a floor.



Friction is the source of the force preventing the motion. If there is
no force that attempts to move an object from the position of rest,
friction results in no force preventing this move, but, if there is a
force that attempts to move an object, friction exhorts a force against
it, thus preventing the move.



If the force that attempts to move an object is not too strong, bumps on
the surfaces of object and its support are still caught between each
other, an object stays in place, which means that the force of friction,
directed against the force that attempts to move an object, is equal to
a force of moving by magnitude and opposite in direction.



Obviously, the force of friction has its limits, so, if a very strong
force attempts to move an object, the bumps on the surface will no
longer be able to hold an object, and an object moves.

So, as the force attempting to move an object from the state of rest
grows in magnitude, so does a force of static friction that prevents
this move, but only up to a maximum value, after which the force of
friction cannot grow any more, and the object moves. This maximum value of the friction force is the one when it is specified explicitly.



To move an object from the position of rest we have to apply force. The
heavier an object - the deeper bumps on its surface are caught
in-between bumps of the surface it stands on. Therefore, the force
needed to move it from the position of rest depends on an object's
weight. At the same time, surfaces can be more or less smooth, that is
they can have deeper or shallower bumps. Obviously, the degree of
smoothness must be a factor in the amount of force needed to move an
object from the position of rest.



So, two major factors contribute to the amount of force needed to shift
an object from the position of rest: the pressure between an object and a
surface it stands on (for example, the component of its weight) and the
quality of surfaces of an object and its support.



According to numerous experiments, for any two surfaces (surface of an object and surface of a support it rests on) there is a coefficient of static friction μ, such that the force needed to shift an object from the position of rest F depends on this coefficient and the normal pressure N between an object and its supporting surface as

F = μ·N



If the experiment is conducted on Earth and the supporting surface is horizontal, normal pressure of an object is its weight.

If the surface is an incline, the vector of weight should be represented
as a combination of a normal to a supporting surface and tangential to
it components. The normal component contributes to friction, while the
tangential component represents the force that attempts to move object
from the position of rest.



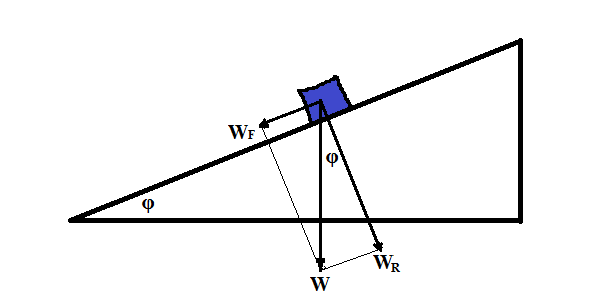
Consider an incline of angle φ and an object of weight W on it. Will it slide down?



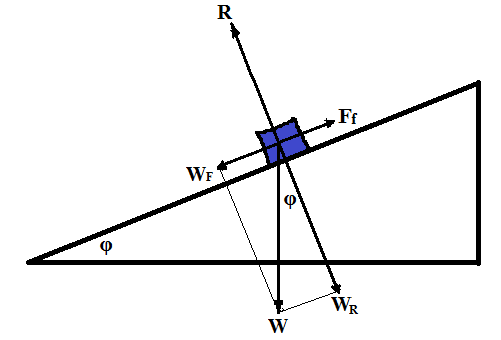
The following forces are acting upon this object:

(a) vector of gravity of Earth W directed vertically down;

(b) reaction of the surface R directed perpendicularly to a surface of an inclined;

(c) force of static friction F_f directed against potential movement down the slope.

The right approach to analysis of this experiment is to represent a vector of weight W as a combination of a vector perpendicular to an inclined W_R and the vector of force attempting to move an object down a slope W_F.

Now the only force that attempts to move an object is a component of its weight tangential to an inclined W_F.

The reaction force R equals to a component W_R of weight.


Obviously, the magnitudes of these vectors are:

W_F = W·sin(φ)

W_R = W·cos(φ)

Assuming, we know that the coefficient of static friction equals μ. Then the maximum force of static friction equals to

F_f = W·cos(φ)·μ



Therefore, if W_F is greater than F_f, the object will slide down a slope, otherwise the static friction will be able to hold it in place.

The minimum angle when the movement occurs is a solution of the following equation for angle φ:

W·sin(φ) = W·cos(φ)·μ or

tan(φ) = μ or

φ = arctan(μ)

This is an angle, when the sliding of an object under its own weight begins.



Kinetic Friction



Kinetic friction is the friction between a moving object and
surface it moves on or between surfaces of two touching each other
objects moving relative to each other.



Generally speaking, we all know that it's easier to move a sofa on the
floor after the movement has started than to initiate a movement from
the state of rest.



The theory behind the friction, based on tiny bumps on the surfaces of
touching each other objects, explains this as a result of deeper
penetration of bumps of one surface between the bumps of another, when
objects are at rest, than when objects are in motion and bumps have
little time to deeply penetrate each other, they slide across each
other, causing kinetic friction, which is less than static.

These bumps are so small that relative speed of one object against another plays little role in the strength of kinetic friction, but the pressure between the objects and material their surfaces are made of are very important.



Quantitatively, kinetic friction is very much like static one with the only difference in the coefficient of friction.

According to numerous experiments, for any two surfaces there is a coefficient of kinetic friction μ, such that any moving object experiences the force F, acting against its movement, which depends on this coefficient and the normal pressure N between an object and its supporting surface as

F = μ·N



This is an experimental law. Coefficients of friction are measured for
many pairs of surfaces, which allows to solve such problems as to find
the distance of breaking from some speed to full stop, determine forces
needed to overcome the friction to move an object with constant speed
etc.

These are the problems we will solve in the next lectures.

Unizor - Physics4Teens - Mechanics - Dynamics - Conservation of Momentum

Notes to a video lecture on http://www.unizor.com



Conservation of Momentum



In the differential form relationship between vectors of momentum of motion and impulse of force causing this motion is

d[m·v(t)] = F(t)·dt

The same can be expressed in terms of derivative of momentum by time:

d[m·v(t)]/dt = F(t)

or, using different notation for derivative,

[m·v(t)]' = F(t)



Any of the above equations are equivalent to the Newton's Second Law.



A trivial consequence of these equations is that in case of absence of force (F(t)=0) the momentum's derivative is zero and, therefore, momentum remains constant.



If we have a system of objects with no external forces, any force,
acting from some object against another has equal in magnitude and
opposite in direction reaction force acting from the latter to the
former. Since the time of interaction is the same for action and
reaction, while forces are equal in magnitude and opposite in direction,
their vectors of impulses, if added, produce zero total impulse. Each
impulse produces a corresponding change in momentum of an object it's
applied against. These momentums will also be of the same magnitude and
opposite in direction. Consequently, the total momentum of the system
will not change.

We can conclude that in the absence of external forces the momentum of motion of a system of objects is constant.

This is the Law of Conservation of Momentum.



Example 1



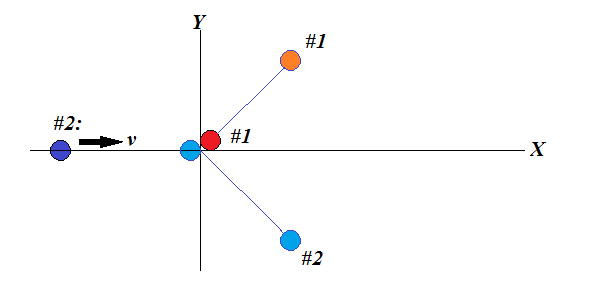
Consider a frame of reference fixed on a billiard table.

A ball #1 is positioned near the origin of coordinates in the middle of a table.

Another ball #2 of the same mass is positioned at some point on the X-axis on its negative side.

A player hits ball #2 towards the point where ball #1 is located, giving it a speed v.

After the contact the balls went each in its own direction. Ball #1 went at an acute positive angle α from the positive direction of the X-axis (that is, counterclockwise), while ball #2 went at an acute but negative angle −β from the positive direction of the X-axis (that is, clockwise).

What are the magnitudes of the speeds of the balls after contact (ignore the friction)?



Solution

Let's apply the Law of Conservation of Momentum.

Initially, the total momentum of the system was equal to the momentum of
ball #2 (as the only one having non-zero velocity), which is P = m (kg)·v (m/sec).

As a vector, it has only X-component not equal to zero, since velocity of ball #2 is along the X-axis.

After the contact the balls have velocities v₁ (for ball #1) and v₂ (for ball #2) with unknown magnitudes, correspondingly, v₁ and v₂.

These velocities, as vectors, have both X- and Y-components:

v_1x = v₁·cos(α)

v_1y = v₁·sin(α)

v_2x = v₂·cos(−β) = v₂·cos(β)

v_2y = v₂·sin(−β) = −v₂·sin(β)

The sum of X-components of momentums of both balls after the contact
must be equal to X-component of the momentum of ball #2 before the
contact and the sum of Y-components of momentums of both balls after the
contact must be equal to Y-component of the momentum of ball #2 before
the contact. that gives us two equations with unknown:


m·v₁·cos(α)+m·v₂·cos(β) = m·v

m·v₁·sin(α)−m·v₂·sin(β) = 0



Reducing by m both equations, we have a simple system of two linear equations with two unknowns:


v₁·cos(α) + v₂·cos(β) = v

v₁·sin(α) − v₂·sin(β) = 0



Solutions for this system are:

v₁ = v·sin(β)/sin(α+β)

v₂ = v·sin(α)/sin(α+β)



Interesting particular case appears if α=0, that is when
the ball #2 hits the ball #1 heads-on. Then the speed of the ball #2
after the contact is zero, it stops at the place of contact and the ball
#1 takes on the full speed v, that the ball #2 used to have, and continues the motion in the same direction along the X-axis.





Example 2

Consider an inertial system of reference on a plane.

Object A moves along X-axis from the negative side of the X-axis in the positive direction towards the origin of coordinates.

Object B moves along Y-axis from the negative side of the Y-axis in the positive direction towards the origin of coordinates.

The mass of object B is 4 times greater than mass of object A, but the
speed of object A along X-axis is 3 times greater than speed of object B
along Y-axis.

At the origin of coordinates these two objects meet and attach to each
other, forming a new combined object AB. The magnitude of the speed of
the combined object AB is v_AB.

What are the speeds of objects before their contact?



Solution

Let the unknown mass of object A be m_A and its speed along the X-axis be v_A.

Let the unknown mass of object B be m_B and its speed along the Y-axis be v_B.

We will deal with scalar speeds because the direction of the velocities
is along the coordinate axes and, therefore, Y-component of the velocity
of object A is zero, as well as X-component of the velocity of object
B.

The vector of momentum of object A before contact is directed along the positive direction of the X-axis and its magnitude is

P_Ax = m_A·v_A

The Y-component of the momentum of object A is zero:

P_Ay = 0

For object B the momentum before the contact is directed along the positive direction of the Y-axis and its magnitude is

P_By = m_B·v_B

The X-component of the momentum of object B is zero:

P_Bx = 0

After the contact and attachment the momentum of the combined object AB is equal by magnitude (with unknown direction) to

P_AB = (m_A+m_B)·v_AB

While we do not know the direction of the velocity of the combined
object AB, we can evaluate the X- and Y-components of its momentum as
sums of corresponding X- and Y-components of momentums of objects A and
B.

From the Law of Conservation of Momentum follows

P_Ax+P_Bx = P_ABx

P_Ay+P_By = P_ABy

Therefore,

P_ABx = m_A·v_A

P_ABy = m_B·v_B

From these two orthogonal components we can derive the magnitude of the momentum vector of combined object AB:
|P_AB| = √[m_A·v_A]² + [m_B·v_B]²

On the other hand, the mass of combined object AB is a sum of masses of
objects A and B. Also, the magnitude of a speed of combined object v_AB is given.

Therefore,

(m_A+m_B)·v_AB =

= √[m_A·v_A]² + [m_B·v_B]²

We know that

m_B = 4·m_A

v_A = 3·v_B
Substituting these proportions to the equation above for the momentum of combined object AB, we obtain

(m_A+4·m_A)·v_AB =

= √[m_A·3·v_B]² + [4·m_A·v_B]² =

= 5·m_A·v_B

Reducing both sides of the equation by 5·m_A, we obtain the value of speed of object B:

v_B = v_AB

Now we can determine speed of object A:

v_A = 3·v_B = 3·v_AB

Unizor - Physics4Teens - Mechanics - Dynamics - Impulse of Force

Notes to a video lecture on http://www.unizor.com



Impulse



In a simple case of a single constant force F acting in the direction of motion on an object of mass m that moves with constant acceleration a the Newton's Second Law states that

F = m·a



Let's assume that at moment of time t the speed of this object was v and at moment of time t+Δt the speed of this object was v+Δv.

Since an objects moved with constant acceleration a, the average increment of speed during this time should be equal to the acceleration multiplied by increment of time

(v+Δv) − v = a·[(t+Δt) − t] or

Δv = a·Δt



Multiplying both sides of the above equation by mass m, we obtain

m·Δv = m·a·Δt or

m·Δv = F·Δt

Considering m is constant, we can make the following manipulations with the left side of this equation:

m·Δv = m·[v(t+Δt)−v(t)] =

= m·v(t+Δt)−m·v(t) = Δ(m·v)

Therefore,

Δ(m·v) = F·Δt

The expression on the left side represents an increment of the momentum of motion. The expression on the right side is called impulse of the force F acting on an object during interval of time Δt.



If the time interval Δt is infinitesimal, this can be applied to variable force F(t) and written in terms of differentials

d(m·v) = F(t)·dt



Integrating this equality by time t, we obtain on the left side the total momentum change during time from moment of time t=t₁ to moment t=t₂:

P = ∫_t1^t₂d(m·v) =

= m·v(t₂) − m·v(t₁)



The total impulse exhorted by a variable force F(t) during this time from t₁ to t₂ is

J = ∫_t1^t₂F(t)dt



Hence, our qualitative observation, that the force acting on an object
changes its velocity, can be quantitatively characterized as impulse exhorted by a force during certain time period equals to change of momentum during this period.



Obviously, for a simple case of constant force F this is equivalent to

m·v(t₂) − m·v(t₁) = F·(t₂−t₁)

which fully corresponds to the Newton's Second Law for constant force F and, therefore, constant acceleration a since

[v(t₂)−v(t₁)]/(t₂−t₁) = a = F/m



Generally speaking, force is a vector. So is velocity and, therefore, momentum of motion. All the definitions discussed above, considering forces and motions in our three-dimensional space, are for vectors.

Hence, for constant force F in three-dimensional space the definition of impulse of this force acting during time t is: J = F·t.

For variable force F(t) acting on object from moment of time t=t₁ to moment of time t=t₂ we define the impulse in the integral form

J = ∫_t1^t₂F(t)dt

where integral of vector is a vector of integrals of its X-, Y- and Z-components.



Using the approach based on the concept of impulse of the force and momentum of motion, we can simplify solutions to some problems.

Consider a case when an object of mass m, staying at rest in some inertial reference frame, is pushed forward with constant force F₁ during time t₁, then with force F₂ in the same direction during time t₂.

What would be its final speed v_fin?

The impulse given by the first force is F₁·t₁. It caused an increase in speed from 0 to v₁.

Therefore,

F₁·t₁ = m·(v₁−0)

Then the impulse given by the second force is F₂·t₂. It caused an increase in speed from v₁ to v_fin (the final speed).

Therefore,

F₂·t₂ = m·(v_fin−v₁)

Adding them together, we obtain

F₁·t₁ + F₂·t₂ =

= m·v₁ + m·(v_fin−v₁) =

= m·(v_fin−0) = m·v_fin

which gives the final speed

v_fin = [F₁·t₁ + F₂·t₂] /m

But the easiest way to solve this is to use combined impulse given to an
object as the cause of increased speed from zero to its final value v_fin by adding impulses F₁·t₁ + F₂·t₂ and equating their sum to final increase in momentum m·v_fin with the same result for final speed.



SUMMARY

Any action of force on an object during certain time interval exhorts an impulse that causes to change the object's momentum.

Each consecutively or simultaneously applied impulse contributes to this
change of momentum, so the final momentum of an object is the combined
effect of all impulses acting on it in an integrated fashion.




Example

Liquid fuel is pumped into combustion chambers of airplane engines at the rate μ (kg/sec).

Burned gases are exhausted with speed v_out. An airplane is in uniform motion along a straight line with constant velocity.

What is the force of air resistance acting against its motion?

Assume that the mass of an airplane is significantly greater than the
mass of exhausted gases, so we can ignore the loss of mass during
engine's work.



Solution

Airplane is in uniform motion, which allows us to use a reference frame
associated with it as the inertial frame, where the Newton's Laws are
held and all calculations can be done.

Since an airplane's motion is uniform, the sum of the vector of air
resistance force, directed against its movement, and the vector of the
reaction force from the gases, exhausted by its engines and directed
towards its movement, should balance each other and be equal in
magnitude since their directions are opposite.

During time interval Δt the engines exhaust burned gases of mass Δm=μ·Δt, accelerating them from speed zero to v_out and correspondingly increasing their momentum.

Therefore, from the equality between the increment of momentum of motion of burned gases and the impulse of force applied to them by the engines, we have the following equality:

Δm·v_out = F··Δt

Using the expression for Δm above, we derive from this

μ·Δt·v_out = F··Δt

And the value for the force produced by an engine applied to burned gases pushing them backward

F = μ·v_out

According to Newton's Third Law, this is the same force, with which burned gases push an airplane forward.

Since the airplane movement is uniform, the air resistance is also equal in magnitude to this value.

Unizor - Physics4Teens - Mechanics - Dynamics - Momentum of Motion

Notes to a video lecture on http://www.unizor.com



Momentum of Motion



In a simple case of a single constant force F acting in the direction of motion on an object of mass m that moves with constant acceleration a the Newton's Second Law states that

F = m·a



Let's assume that at moment of time t the speed of this object was v and at moment of time t+Δt the speed of this object was v+Δv.

Since an objects moved with constant acceleration a, the average increment of speed should be equal to the acceleration multiplied by increment of time

(v+Δv) − v = a·[(t+Δt) − t] or

Δv = a·Δt



Multiplying both sides of the above equation by mass m, we obtain

m·Δv = m·a·Δt or

m·Δv = F·Δt or

m·(Δv/Δt) = F



If the time interval Δt is infinitesimal, this can be written in terms of derivative of speed v by time t as

m·(dv/dt) = F

or, since mass m is constant,

d(m·v)/dt = F



So, the force F equals to a derivative by time of the value of a product of mass by speed m·v, called momentum of motion.

Since we have reduced the time interval Δt to
infinitesimal value, it's no longer important that the force and
acceleration are constant. In the next moment of time it can be
different, but at any moment of time the dependency between the force
and a derivative of the momentum above will take place.



Let's consider a more complicated case of motion in the three-dimensional space.

The Newton's Second Law states that the vector of force F(t), as a function of time t, equals to a product of constant mass m and the vector of acceleration a(t), which, in turn, also depends on time t:

F(t) = m·a(t)



An immediate consequence from this, considering the vector of acceleration is a derivative of vector of velocity v(t), is the following chain of equalities:

F(t) = m·a(t) = m·dv(t)/dt =

= d(m·v(t))/dt

from which we conclude that the force F(t), acting on an object, is a derivative by time of the characteristic of motion called momentum, that is equal to m·v(t):

F(t) = [m·v(t)]^I



The same equality can be expressed in term of infinitesimal increments:

F(t)·dt = d(m·v(t))

The left side of this equation is an increment in impulse of the force F(t) during the time from t to t+dt, while the right side represents an increment of the momentum of object of mass m moving with velocity v(t) during the same time interval.



Let's return to a simple case of a constant force acting in the direction of movement with an equation that connects the force with a derivative of momentum:

d(m·v)/dt = F

The first consequence from this equation is that in the absence of force (F=0)
the derivative of momentum is zero and, therefore, momentum is
constant. With constant mass it is equivalent to the Principle of
Inertia because it implies the constant velocity.

But, expressed as a constant momentum, it covers a more general case of complex systems of objects with no external forces.



Assume that a two-stage rocket of mass m flies in open space far from any gravity fields along a straight line with speed v
with no engine working. According to the Principle of Inertia (and the
Newton's First Law), it will move like this indefinitely.

Then at some moment the first stage of mass m₁ is separated from the second stage of mass m₂=m−m₁. This separation is achieved by pushing the first stage back along the same straight line with a force F during time t.

The resulting speed of the first stage is

v₁ = v − (F/m₁)·t

The resulting momentum of the first stage is

m₁·v₁ = m₁·v − F·t

Meanwhile, according to the Newton's Third Law, the same by magnitude
force should push the second stage forward during the same time. Its new
speed is

v₂ = v + (F/m₂)·t

The momentum of the second stage is

m₂·v₂ = m₂·v + F·t

Let's add the momentums of two stages after the separation:

m₁·v₁ + m₂·v₂ =

= m₁·v − F·t + m₂·v + F·t =

= (m₁ + m₂)·v = m·v



As we see, even in case of a complex system of objects with no external forces, the momentum of an entire system is constant.

Our example with a rocket can be generalized into a system of any number
of objects and not only straight line motion. We will address this
issue further in the course as the Law of Conservation of Momentum.

Unizor - Physics4Teens - Mechanics - Dynamics - Superposition of Forces ...

Notes to a video lecture on http://www.unizor.com



Superposition of Forces -

Problems 2



Problem A



Consider a slope that makes an angle θ with the ground. On
the top of this slope there is a pulley, through which goes a
weightless non-stretchable thread that connects two point-objects:

one of mass M₁, sliding up the slope, and

another of a bigger mass M₂, hanging off the top pulley vertically down and pulling the thread down, thus forcing the smaller object to go up the slope.



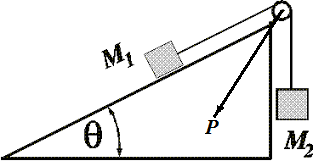
Determine the direction and magnitude of the pressure vector P on the pulley's axis.



Answer:



Direction of the vector of pressure on the pulley's axis P is along the angle bisector of the angle at the top of a pulley.

The magnitude of this vector is

P = k·[1+sin(θ)]·cos(π/4−θ/2)

where

k = 2M₁·M₂·g / (M₁+M₂)





Problem B



A point-object is hanging on a thread of length L and is uniformly moving along a circular trajectory in a horizontal plane, while a thread always maintains a constant angle φ with a vertical.



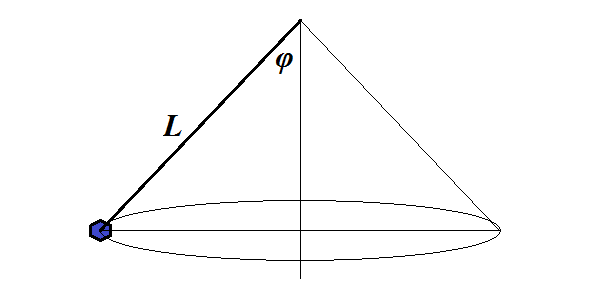
How many loops N(t) this object does in time t?



Answer:



N(t) = (t/2π)·√g/[L·cos(φ)]

where g is a free fall acceleration.





Problem C



A wedge of mass m and angle 2φ slides down between two point-objects of mass M each, pushing them apart without any friction.



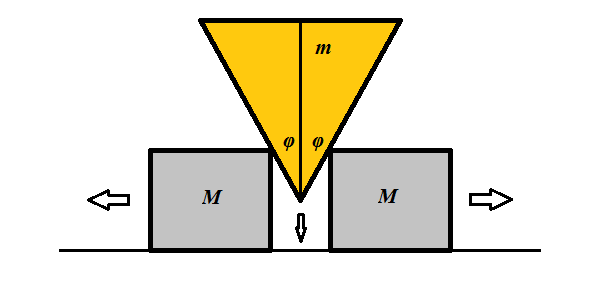
Find the acceleration a of each of the two objects that a wedge pushes apart.



Answer:



a = g·tan(φ)/

/[1+2(M/m)·tan²(φ)]





Problem D

During long jump competition a sportsman accelerates with constant acceleration a during time t and then jumps vertically up.

During his jump he goes up to height h, while continuing moving forward because of his initial horizontal speed he gained before jumping.

What is the length L of his jump?



Answer:

L = 2a·t·√2h/g

Unizor - Physics4Teens - Mechanics - Dynamics - Superposition of Forces ...

Notes to a video lecture on http://www.unizor.com



Superposition of Forces -

Problems 1



Problem A



A boat stands still in the middle of a river. It is tied to a river bank by a rope of the length L.

The river flow pushes it with the force F downstream, and the wind pushes it with the force 0.75·F perpendicularly to the river flow away from the bank.

(a) What is the force of tension P of the rope?

(b) What is the distance d from the river bank to the boat?



Answer:

(a) P = 1.25·F

(b) d = 0.6·L





Problem B



An object of mass m and, therefore, of weight at the ground W=m·g, where g
is a free fall acceleration, moves with constant linear speed on a
bridge, that has a shape of an arc with upward convexity of a radius R.

(a) Determine the speed v of an object as a function of pressure P it produces on the bridge at the top of the arc.

(b) At what speed v₀ the object will become "weightless" at the top of the bridge's arc?



Answer:

(a) v = √R·(g − P/m)

(b) v₀ = √R·g,

because "weightlessness" is a state when an object does not press on the support and, therefore, P=0





Problem C



A point object of mass m and, therefore, of weight W=m·g, where g is a free fall acceleration, is hanging on the end of a weightless thread of length R,
fixed at the other end at some point, and can freely move like a
pendulum within a vertical plane that we can take as the XZ-plane of
coordinates with origin at the point where a thread is fixed.

An object's initial position is with its thread making an angle φ from a vertical.

(a) What is the tension of a thread P in the initial position?

(b) What is the vector of force F acting on an object in its initial position in the direction of its motion along a circular trajectory?



Answer:

(a) Tension P = m·g·cos(φ)

(b) Force along the trajectory F = m·g·sin(φ)





Problem D



A projectile is launched from the wall of the castle horizontally towards the army that laid a siege on this castle.

The height of the castle wall is H, the horizontal speed of a projectile is v.

The free falling acceleration caused by gravity is g.

Ignore the air resistance.

(a) What is the time t_Land the projectile will be in the air until landing?

(b) What is the distance d of a point the projectile lands from the bottom of the castle wall?

(c) What is the magnitude of a speed of the projectile v_Land at the moment of landing?



Answer:

(a) t_Land = √2H/g

(b) d = v·√2H/g

(c) v_Land = √v² + 2Hg

Unizor - Physics4Teens - Mechanics - Dynamics - Resultant Force

Notes to a video lecture on http://www.unizor.com



Resultant Force



According to the Principle of Superposition of Forces, we can replace actions of many forces acting upon a point-object (each one being a vector) with a vector sum of these forces (called resultant force), getting exactly the same effect on the motion of a point-object.



An immediate consequence from the Principle of Superposition of Forces
is that any single force acting upon a point-object can be replaced by a
vector sum of a few forces, which produce exactly the same effect on
the motion of a point-object, as long as this vector sum of forces
exactly equals to the vector of original force.



We will demonstrate this Principle on a few examples.





Example 1



In the frame of reference associated with the ground we have a point-object sliding down a slope.

Given are: mass of an object m, force of gravitation of this object (its weight, directed vertically down) W and an angle φ between a slope of a slide and horizontal ground.

Our task is to determine the acceleration of this object on its
trajectory down a slope, considering there is no friction that slows
down the object's movement down a slope.



Solution



Trajectory of our object is a straight line (the slope), mass m
is known, so all we need to find the acceleration from the Newton's
Second Law is the force that pushes this object along its trajectory
down a slope.

Obviously, the slope's angle φ plays an important role here. Consider a slope with φ=0, that is the "slope" is not really a slope, but a horizontal plane. The object will not move then because its weight W, directed vertically down perpendicularly to a horizontal plane, is completely balanced by the reaction force of the plane R
directed vertically up and equal in magnitude to the weight, according
to the Newton's Third Law. The resultant force is zero-vector and there
is no acceleration.

On the other extreme, if our slide is vertical with φ=90°, an object does not press on it, there is no reaction force, all the object's weight W is directed along the vertical trajectory downward, and the acceleration can be determined from the Newton's Second Law as a=W/m.



To meaningfully include the slope's angle φ into our calculation, we will represent its weight W as a vector sum of two forces:

(a) the force W_R, directed perpendicularly to a slope, causing slope's reaction force R to balance it, and

(b) the force W_F, directed parallel to a slope, pushing the object forward along its trajectory and causing its acceleration.

If we succeed in such representation, we will say that the force W_F is the one and only force that pushes the object of mass m down a slope and can be used to determine the object's acceleration from the Newton's Second Law as a=W_F/m.



This representation of the weight of an object as a sum of two vectors W=W_R+W_F, knowing the angle φ, is easy.


The magnitude of vectors W_R and W_F, which we will denote as W_R and W_F correspondingly, equal to

W_R = W·cos(φ)

W_F = W·sin(φ)

where W is the magnitude of a vector of weight W.



The force W_R
is completely balanced by the reaction force of the slope (they both
are perpendicular to a slope, equal in magnitude and oppositely
directed, according to the Newton's Third Law).

So, the only force affecting the motion of an object on its trajectory down a slope and acting along this trajectory is W_F, the magnitude of which we have calculated above.

Therefore, an acceleration of an object down a slope will be a vector directed parallel to a slope with a magnitude

a=W·sin(φ)/m.





Example 2



A motorcycle stuntman decides to demonstrate his skills by going inside a vertical loop.

His mass is m.

His linear speed inside this loop is v.

The magnitude of the gravity force (his weight with a motorcycle) is W.

The radius of a loop is R.

Find the pressure on the loop at its top and at its bottom from a moving motorcycle.



Solution



Let's set our frame of reference on the ground with Z-axis directed upward and a loop being in the XZ-plane.



Since an object of mass m moves with a constant linear speed v along a circular trajectory of radius R,
there is a force that keeps it on this trajectory. This force is always
directed towards the center of a circle and is equal in magnitude to m·a, where a is a magnitude of its acceleration towards a center of a circle called centripetal acceleration.

From the Kinematics of rotation we know that a=R·ω², where ω is the angular speed of rotation and is related to linear speed of rotation v as v=R·ω.

From this we derive the centripetal acceleration a in terms of linear speed and radius: a=v²/R.



Knowing the force that keeps an object on a circular trajectory, let's analyze what is the source of this force.

On one hand, there is always a weight directed downward (towards negative direction of Z-axis) and equal in magnitude to W.

On the other hand, an object presses onto the loop with the force P(t)
perpendicularly to the loop, and the loop reacts back unto object with
the same by magnitude but oppositely directed reaction force. This
reaction force is directed upward, when the object is at the bottom of
the loop (we will denote its magnitude as P_b), or downward, when an object is at the top (we will denote its magnitude as P_t).



The combination of weight and the reaction force of the loop is the
resultant force that keeps the object on its circular trajectory.



Therefore, at the bottom of the loop, when weight is directed downward,
reaction is directed upward and the centripetal force is directed
upward,

−W+P_b = m·R·ω²



At the top of the loop, when weight is directed downward, reaction is
directed downward and the centripetal force is directed downward,

−W−P_t = −m·R·ω²



From the first equation we can derive the reaction force at the bottom
that is, by magnitude, equals to the pressure on a loop at this point:

P_b = m·R·ω² + W

From the second equation we can derive the reaction force at the top
that is, by magnitude, equals to the pressure on a loop at this point:

P_t = m·R·ω² − W



Theory of gravitation, that will be studied later in this course, states
that weight is a force of gravity proportional to a product of masses
of a planet and an object on its surface and inversely proportional to a
square of a distance between centers of mass. The latter is
approximately equal to a radius of a planet.

For Earth it is expressed as W = m·g, where constant g is an acceleration of the free falling on Earth, which is equal to 9.8 m/sec².

On Jupiter, by the way, this constant - free fall acceleration - is equal to 25 m/sec².

Using this, we can write our formulas for pressure as follows:

P_b = m·R·ω² + m·g = m·(R·ω² + g)

P_t = m·R·ω² − m·g = m·(R·ω² − g)



It should be noted that, while P_b is always positive, P_t
might be negative, if the speed of an object is not sufficient. If
negative, the movement will not be circular and object will fall down
from its trajectory.



If R·ω²=g or ω=√g/R, or v=√g·R,
the object will experience weightlessness at the top position, since it
will not press onto loop and, therefore, loop will not press on it. For
loop of, say, 10 meters in diameter (R=5 m) linear speed of approximately 7 m/sec
will produce an effect of weightlessness at the top of a loop. This
linear speed with a given radius of a loop is equivalent to the angular
speed of 1.4 rad/sec or about one complete loop in 4.5 second.

Slower speed will result in falling from the circular trajectory.  

Unizor - Physics4Teens - Mechanics - Dynamics - Superposition of Forces

Notes to a video lecture on http://www.unizor.com



Sum of Forces



Previously, in most cases we were analyzing the motion of objects with only one force participating in the process.

With few exceptions our objects moved either along a straight line with a
force acting along this line or rotated around some center with only
one force keeping them on their circular trajectory.
A couple of problems related to launching of projectile at an angle to
horizon did deal with a more complex motion, but even in this case there
was only one force - gravity - that acted on an object.



This lecture is dedicated to general approach to dealing with multiple
forces of different types acting simultaneously on the same object.

Let's review what kind of forces occur in real life and, therefore, might affect the motion of an object.



Applied Forces

These are forces caused by one object contacting another (pull, push, roll etc.).

These are the first kind of forces people dealt with and understood
relatively well in a sense that they always saw the source of them.

A car moves because its engine pushes the wheels forward. A person walks
because his muscles make his legs move in a special way to push back
the road.



Friction

The effect of friction is slowing down the movement, unless additional
forces are applied. The source of friction is non-ideal contact between a
moving object and its surrounding, that causes tiny bumps between them
catch each other, thus preventing the uniform motion.

To the same category we can put resistance of air, when a plane flies in
a sky or resistance of water, when a submarine moves in the deep sea.



Tension

If you pull a cart by a rope, you pull the rope, not a cart. That force
somehow is transferred to a cart. The mechanism of transferring a force
from one end of a rope to another is tension. Your force of
pulling attempts to stretch a rope, but internal links within a rope do
not allow it to stretch, one link is attached to another and transfers
the force down to all tiny links inside the rope. That causes the rope
to become tense, and the force you applied to one end of the rope is the
cause of the rope's tension, which, in turn, pulls the cart.



Elasticity

Elasticity is a property of an object, like spring or rubber, to change
its form under some external force and then restore the original form,
when the force is no longer applied. If an object stretches with its
weight a vertically positioned spring with fixed top end, reaching some
fixed balanced position, it is the elasticity force of a spring that
counteracts the force of the object's weight, thus holding an object in a
fixed position.

The cause of elasticity is in the inner structure of a material. Steel
of spring is such an elastic material, as well as rubber and others.



Gravitation

Any two masses attract ("gravitate") each other. The attraction is
mutual, the force of gravitation of object A towards object B is
directed from A to B and is equal in magnitude, but opposite in
direction, to the force of gravitation of object B towards object A,
directed from B to A.

Earth attracts everything on it, like people, houses, airplanes in the
sky, ships in the sea, while each of them attract Earth with the same in
magnitude, but opposite in direction force.

Quantitatively, the force of gravitation between two masses proportional
to each mass and inversely proportional to square of distance between
them. This is an experimental fact, we'll discuss it later in this
course.



Electricity

This force is in some way similar to gravitation, but in case of
gravitation we have only one type of force - attraction, while in case
of electricity it might be attraction or repelling, depending on what
kind of electrical charges we deal with.

Two electrically charged objects with opposite charges (which we call
"positive" and "negative") attract each other similarly to gravitation.

Quantitatively, the force of electrical attraction between two
electrically charged objects is proportional to each charge and
inversely proportional to square of distance between them. This is an
experimental fact, we'll discuss it later in this course.

If two positively or two negatively charged objects are involved, the
forces will act in opposite direction, the objects will be repelled from
each other with the force of repelling exactly the same in magnitude as
the force of attraction in case of two opposite charges.



Magnetism

This force is in some way similar to electricity, but in case of
electricity we have two types of objects - positively and negatively
charged, while in case of magnetism each magnetized object has two ends
- two "poles" with opposite "polarity". There are two kinds of
polarity, that we conditionally call "North" (N) and "South" (S), and
opposite ones (N - S) attract each other, while similar ones (N - N or S
- S) repel.

Two magnetized objects attract or repel each other, depending on which side of one object is close to which side of another.

Quantitatively, the force of magnetic attraction or repelling between
two magnetized objects is proportional to degree of their magnetizing
and inversely proportional to square of distance between them. This is
an experimental fact, we'll discuss it later in this course.



So, there is a multitude of forces that can act on our object
simultaneously and we have to be able to analyze their combined effect
on the motion.

The main idea of a motion, when multiple forces act on an object, is a principle of superposition of forces.



It is experimentally confirmed and accepted in classical Physics as an
axiom that, if two or more forces act on the same object at the same
time, the object moves identically to the movement caused by only one
force, that is a vector sum of all individual forces acting on an
object.



This axiom is called Principle of Superposition of Forces.



Here we are talking about general principle, that we accept for any kind
of forces in three-dimensional world, each being a vector: acting together, these forces produce the same effect, as if they are all replaced by one force - their vector sum.



Let's illustrate this with a couple of examples.



1. When a rocket is launched vertically up, there are two major forces
acting upon it: the force of gravity pulls it down and its engine pushes
it up (stronger than gravity, of course). These two forces are directed
along the same vertical line, but opposite in direction. Their vector
sum is directed upwards and quantitatively is determined by a vector sum
of these major components.



2. A car moves up the hill and is acted upon by three forces:

gravity pulls it downward,

its engine pulls uphill and

the reaction of the road pushes perpendicularly to the road.

The vector sum of these three forces must point up the hill.



3. An object is hanging on a thread fixed to a point on a ceiling and is moving in a vertical plane like a pendulum.

There are two forces acting upon it at each moment:

gravity pulls it downward,

tension of a thread pulls it towards the point on a ceiling, where a thread is fixed.

The vector sum of these two forces must be tangential to an arc of
trajectory of this object and directed towards this arc's midpoint.



All the above examples are examples of the Principle of Superposition of Forces
- a universal principle of Physics, which we accept as an axiom,
regardless of the physical nature of the forces involved, and which is
confirmed by experiments.  

Unizor - Physics4Teens - Mechanics - Dynamics - Forces - Problems

Notes to a video lecture on http://www.unizor.com



Forces - Problems



Problem 1



A car of mass m uniformly accelerates from a state of rest to a maximum speed v_max along a straight road during time t_max,

(a) What is the most convenient reference frame to solve this problem?

(b) What is the vector of acceleration a(t) as a function of time?

(c) What is the force F(t) its engine produces to push car forward as a function of time?

(d) What is the vector of velocity v(t) as a function of time?

(e) What is the distance d(t) it covers as a function of time?



Answers:



(a) Reference frame:

Origin at the beginning position of a car on a road, X-axis goes along
the road in the direction of car's movement, Y- and Z-axes are in any
position perpendicular to X-axis.

In this frame the Y- and Z-coordinates will always be zero for any moment of time t.

(b) Acceleration: vector directed along the X-axis with magnitude

x"(t) = a = |a(t)| = v_max /t_max

(c) Force: vector directed along the X-axis with magnitude

|F(t)| = m·a = m·v_max /t_max

(d) Velocity: vector directed along the X-axis with magnitude

x'(t) = |v(t)| = a·t = v_max ·t /t_max

(e) Distance:

x(t) = d(t) = a·t²/2 = v_max ·t²/(2·t_max)



Checking:



Acceleration must be constant:

x"(t) = v_max /t_max

(does not depend on t)

At t=0 distance from the beginning position must be zero:

x(0) = v_max ·0²/(2t_max) = 0

At t=0 vector of velocity must have magnitude of zero:

x'(0) = v_max ·0/t_max = 0

At t=t_max vector of velocity must have magnitude v_max:

x'(t_max) = v_max ·t_max/t_max = v_max





Problem 2



Exactly the same as Problem 1 above, except in the beginning at time t=0 a car is not at rest, but moves with speed v_min.



Answers:



(a) Reference frame:

Origin at the beginning position of a car on a road, X-axis goes along
the road in the direction of car's movement, Y- and Z-axes are in any
position perpendicular to X-axis.

In this frame the Y- and Z-coordinates will always be zero for any moment of time t.

(b) Acceleration: vector directed along the X-axis with magnitude

x"(t) = a = |a(t)| = (v_max−v_min)/t_max

(c) Force: vector directed along the X-axis with magnitude

|F(t)| = m·a = m·(v_max−v_min)/t_max

(d) Velocity: vector directed along the X-axis with magnitude

x'(t) = |v(t)| = v_min + a·t = v_min + (v_max−v_min)·t /t_max

(e) Distance:

x(t) = d(t) = v_min·t + a·t²/2 = v_min·t + (v_max−v_min)·t²/(2·t_max)



Checking:



Acceleration must be constant:

x"(t) = (v_max−v_min)/t_max

(does not depend on t)

At t=0 distance from the beginning position must be zero:

x(0) = v_min·0 + (v_max−v_min)·0²/(2·t_max) = 0

At t=0 vector of velocity must have magnitude of v_min:

x'(0) = v_min + (v_max−v_min)·0 /t_max = v_min

At t=t_max vector of velocity must have magnitude v_max:

x'(t_max) = v_min + (v_max−v_min)·t_max /t_max = v_max





Problem 3



A planet of mass m uniformly (that is, with constant angular speed) rotates around its star on a constant distance R from it, making one full circle (that is, 2π radians) in t_o time.

(a) What is the most convenient reference frame to solve this problem?

(b) What is the angular speed ω of a planet as it rotates around its star?

(c) What is the position vector of a planet as it goes along its
circular trajectory in XY-coordinates (Z-coordinate is always 0 for
properly chosen frame of reference)?

(d) What is the vector of velocity of a planet as it goes along its
circular trajectory, and how is this vector directed relative to
position vector?

(e) What is the magnitude of velocity vector (speed) v?

(f) What is the vector of acceleration of a planet as it goes along its
circular trajectory, and how is this vector directed relative to
position vector?

(g) What is the magnitude of acceleration vector a?

(h) Express the magnitude of acceleration vector a in terms of radius of a circular trajectory R and the magnitude of the velocity vector v.

(i) What is the vector of force of gravity from a star to a planet in
terms of mass, radius of trajectory and speed (angular and linear)?



Answers:



(a) Reference frame:

Origin at the center of a star, XY-plane should be a plane where a
planet rotates, Z-axis is perpendicular to XY-plane, X-axis is from a
star to a point where planet is located at moment of time t=0.

In this frame the Z-coordinate will always be zero for any moment of time t.

(b) Angular speed:

ω = 2π/t_o - constant

(c) Position vector {x(t), y(t)}:

x(t) = R·cos(ωt)

y(t) = R·sin(ωt)

(d) Velocity {x'(t), y'(t)}

(first derivative of position):

x'(t) = −R·ω·sin(ωt)

y'(t) = R·ω·cos(ωt)

This velocity vector is perpendicular to position vector since their scalar product x(t)·x'(t)+y(t)·y'(t) equals to zero.

(e) Magnitude of velocity vector (speed):

v = √x'(t)²+y'(t)² = R·ω

(f) Acceleration {x"(t), y"(t)}

(second derivative of position or

first derivative of velocity):

x"(t) = −R·ω²·cos(ωt)

y"(t) = −R·ω²·sin(ωt)

This velocity vector is collinear to position vector, but directed
towards the origin of coordinates because both components have negative
multiplier −ω² in front of them.

(g) Magnitude of acceleration vector:

a = √x"(t)²+y"(t)² = R·ω²

(h) a = v²/R

(i) F = m·a = m·R·ω² = m·v²/R

Unizor - Physics - Mechanics - Dynamics - Newton's Three Laws

Notes to a video lecture on http://www.unizor.com



Newton's Three Laws



Newton's three laws of motion are axioms that we accept to be true in any inertial frame of reference.

As a very good approximation of the inertial frame of reference, we can consider the heliocentric system of coordinates with an origin at Sun and axes directed to stars.

In many cases we will consider geocentric system of coordinates with
origin at the center of the Earth and axes directed to stars or
ground-related system with origin and XY-plane fixed on the ground as
approximately inertial.



Another important consideration is that in their classic formulation the
Newton's laws address the principles of motion of point objects, where
all the mass of an object and all the forces applied to it are
concentrated in one point with three coordinates.

So, the geometric size of the point object is zero, and in most cases we
will omit the word "point", implying it when talking about objects,
unless otherwise is explicitly specified.



First Law



The Newton's First Law is the familiar Law of Inertia that states that an object at rest stays at rest and an object in uniform motion stays in this uniform motion (that is, no change in velocity vector), unless acted upon by unbalanced forces.



Second Law



The Newton's Second Law is the most fundamental law of classic Mechanics. It establishes a quantitative relationship between vector of force F , vector of acceleration a and mass m (scalar) of an object.

These concepts were explained in the previous lecture "Force,
Acceleration, Inertial Mass". The Newton's Second Law brings
quantitative relationship to these concepts as follows.

F = m·a

Notice, this is a vector equation, the force and the acceleration are
vectors. If in certain cases we omit the symbol of vector, the line
across the top, we just assume that the force and the motion, including
the velocity and acceleration, are all occurring along one straight
line.



The above formula is based on the process of establishing the units of measurement for force and mass, described in the previous lecture, and is experimentally confirmed.

Let us recall how we introduced the units of measurement of force and mass.

1. We have taken one particular object (a small cylinder of
platinum-iridium alloy) and said that this object has, by definition,
the inertial mass (or simply mass) of 1 kilogram (kg) - an object of the unit mass.

2. Then we defined any force acting on this cylinder of unit mass and pushing it with an acceleration of 1 m/sec² as being a force of unit magnitude of 1 newton (N) and direction coinciding with the direction of the acceleration.

3. Using the force of unit magnitude of 1 N and applying it to different objects, we defined the mass of any object by the acceleration it gets, if the unit force acts upon it. If the unit force causes it to accelerate with a value a m/sec², its mass, by definition, is 1/a kg. This is because mass was defined as the measure of inertia, hence higher acceleration of an object signifies proportionally smaller inertia and, therefore, proportionally smaller mass.

4. Using the object of unit mass of 1 kg and applying to it different forces, we defined the magnitude of these forces. If the force causes an acceleration of a m/sec² of an object of the unit mass, then, by definition, the magnitude of this force is a (N).



So, we have defined the units of measurement of force and mass in such a way that the Newton's Second Law is true by definition in two simple cases.

Case 1. For the unit of force 1 N and acceleration a(m/sec²) the mass, by definition, is 1/a(kg) and the formula F = m·a is true:

1 (N) = 1/a (kg) · a (m/sec²)

Case 2. For the unit of mass and acceleration a(m/sec²) the force is a(N) and the formula F = m·a is also true:

a (N) = 1 (kg) · a (m/sec²)



It has been experimentally confirmed that mass is additive. That is, if one object has mass m₁ (that is, the force of 1 N gives it an acceleration of 1/m₁ m/sec²) and another object has mass m₂ (that is, the force of 1 N gives it an acceleration of 1/m₂ m/sec²), then a combined object has mass m₁+m₂ (that is, the force of 1 N gives it an acceleration of 1/(m₁+m₂) m/sec²).



It has been also experimentally confirmed that force (as a vector) is additive. That is, if one force is F₁ (that is, an object of 1 kg accelerates by it at a rate |F₁| m/sec² in the direction of this force) and another force is F₂ (that is, an object of 1 kg accelerates by it at a rate |F₂| m/sec² in the direction of this force), then a vector combination of these two forces F₁ +F₂ , applied together to an object of 1 kg will cause the acceleration of this object at the rate |F₁+F₂| m/sec² in the direction of a vector sum of these forces.



In other words, these additive properties of mass and force state that an increase in mass of an object causes proportional decrease in acceleration, if acted by the same force, and an increase in force causes proportional increase in acceleration, if acted on the same object.



Using this additive property of mass and force and the basic equation that defined our units of measurement

1 (N) = 1 (kg) · 1 (m/sec²)

we increase the mass by a factor of m without changing the force, thus decreasing the acceleration by the same factor of m, getting

1 (N) = m (kg) · 1/m (m/sec²)

Then we increase the force by a factor of m without changing the object, thus increasing the acceleration by the same factor of m, getting

m (N)=m (kg) · m/m (m/sec²)=

= m (kg) · 1 (m/sec²)

Then we increase the force again by a factor of a without changing the object, thus increasing the acceleration by the same factor of a, getting

m·a (N) = m (kg) · a (m/sec²)

which means that the force, applied to an object of mass m(kg) and accelerating it with acceleration a(m/sec²) equals to m·a(N), which constitutes the Newton's Second Law.



The above logic is not a rigorous proof but a reasonable foundation for
the Newton's Second Law, which was established experimentally and
accepted as an axiom.


Incidentally, the Newton's First Law (Law of Inertia) follows from the Second Law. Indeed, if force is zero, acceleration is zero as well for an object with non-zero mass.
That means that in the absence of external forces there is no
acceleration and an object stays at rest or moves uniformly with
constant velocity vector, exactly as the Law of Inertia states.



Two important side notes about the Newton's Second Law.

Firstly, more general form of this law, when force and, therefore, acceleration depend on time looks exactly the same:

F(t) = m·a(t)

Secondly, this equation can be considered as a differential equation of the second order since vector of acceleration a(t) is the second derivative of a position vector P(t) :
F(t) = m·d²P(t)/dt²

In coordinate form, where

F(t) = {F_x(t), F_y(t), F_z(t)} and

P(t) = {P_x(t), P_y(t), P_z(t)}

the vector equation is split into three coordinate differential equations of a second order:

F_x(t) = m·d²P_x(t)/dt²

F_y(t) = m·d²P_y(t)/dt²

F_z(t) = m·d²P_z(t)/dt²



Third Law



The Newton's Third Law states that for for every action there is an equal in magnitude and oppositely directed reaction.

In other words, forces are always paired. When object A acts with a force F upon object B, object B acts at the same time upon object A with a force −F .

Notice that these two forces are applied to different objects, the one
originated at A is applied to B, and the one originated at B is applied
to A, and, therefore, strictly speaking, they are not balancing each
other. However, their magnitude is the same and the direction is
opposite to each other.



So, why then a cup on the table is not moving, implying that all the forces acting upon it are balanced?



Consider the following example.

A cup is on a table. It pushes down on a table with its weight (more
precisely, the Earth pulls it down with its gravitation), but nothing
moves, there is no acceleration of either a cup or a table. Why? Because
opposite forces of reaction participate in balancing, counteracting the
force of gravity.

A cup has two balancing forces acting on it: the gravity (its weight,
the force of Earth's gravity that pulls it down) and the reaction of the
table, that is equal in magnitude to the weight and pushes a cup up.
So, the gravity and the reaction of a table, acting upon the same cup,
balance each other, a cup is at rest.

A table is at rest as well because, again, there are balancing forces:
the gravity (table's weight) plus the weight of a cup on a table push
the table down, but the reaction of the floor pushes a table up, thus
balancing the downward forces.



So, forces of action and reaction do not balance each
other, since they are applied to different object. But they do
participate in balancing by nullifying other forces, like gravity.