Unizor - Physics4Teens - Electromagnetism - Electric Current

Notes to a video lecture on http://www.unizor.com

Electric Current

Conductors and Dielectrics

Electric current is a flow of electric charge. Since the actual carrier of electric charge is excess or deficiency of electrons, we need certain material where electrons can travel. So, vacuum cannot be a conductor of electricity because there is no electrons in it, but many metals, like copper, can. But we know that the electrons are orbiting the nuclei of the atoms. So, why do they travel?

The answer is: the force of an external electric field pushes or pulls electrons off their orbits and, as a result, they move inside the material where electric field is present towards or away from the source of the electric field, depending on whether the source is positively (deficiency of electrons) or negatively (excess of electrons) charged.

Consider a copper wire. It contains atoms of copper with 29 electrons in each atom, orbiting on different orbits around corresponding nuclei with 29 protons and from 34 to 36 neutrons in each.
Electrons stay on their orbit until some outside electric field comes into play. When it does, if its intensity is sufficient to push or pull light electrons off their orbits, while heavy nuclei stay in place, these electrons move in one or another direction as a result of different forces acting on them, the major of which is the intensity of the outside electric field. General direction of electrons is defined by the vector of intensity of the electric field. That makes copper a good conductor of electricity.

On the other hand, there are materials, like glass, where electrons are connected stronger to their nuclei, which makes more difficult to push them off their orbits. these materials do not conduct electricity, they are called insulators or dielectrics.

Ideal conductor, connected to an electrically charged object, makes an extension of this object. Since electrons are freely moving between the original object and an attached conductor, both constitute a new object with an electric charge evenly distributed between its parts.
Ideal dielectric, attached to an electrically charged object, does not share its electrons with this object, so the object remains the only one charged.

In practical cases there are no ideal conductors (except under certain conditions of superconductivity under temperatures close to absolute zero) and no ideal dielectrics (except absolute vacuum that has no electrons at all).

Metals are usually good conductors because their nuclei are relatively not easily moved from their places, while electrons are easily pushed off their orbits.
We use this property of conductors to direct the electrons to perform some work, like lighting the bulbs or moving electrical cars.

IMPORTANT NOTICE:
Conductivity is related to movement of electrons and is a measure of how easily electrons are pushed form their orbits by outside electric field.
This should not be mixed with permittivity defined for electric fields and is a measure of propagation of electric field inside some substance.

Electric Current

If the source of the field is a positive charge located near one end of a copper wire, electrons inside the wire would go towards that end. If the negative charge is the source of the field, electrons will move towards the opposite end.

If there is nothing on the opposite end of a copper wire, electrons, after being pushed towards one of the edges, will stop. If, however, there is an opposite charge on the other end of a wire, electrons will move from the negatively charged end to the positively charged one until both charges neutralize each other and whatever end was missing electrons (positively charged) will be compensated by electrons that are in excess on the negatively charged end.

Imagine now that we manage to keep one end of the wire constantly charged positively, while another end constantly charged negatively. Then electrons from the negatively charged end will flow to the positively charged end as long as we can keep these constant opposite charges on both ends. We will have a constant flow of electricity, which is called electric current (or simply current in the context of electricity).

This process of maintaining constant flow of electricity is analogous to maintaining constant flow of water down the water slide using a pump that constantly pumps the water from a pool to the top of a slide, from which it flows down because of the difference in heights and gravity.

While the presence of the electric field is felt almost instantaneously (actually, with a speed close to a speed of light), the electrons that carry electrical charge are not moving from a negatively charged end of a copper wire to the positively charged end with this speed.

A good analogy is the pipe filled with water and a pump connected to one of its ends. As soon as the pump starts working, the water it pumps starts its trip along the pipe and pushes the neighboring molecule of water. Those, in turn, push the next ones etc. So, the water will come from another end of a pipe almost instantaneously (actually, after a time interval needed for the sound waves in the water to cover the length of a pipe), but it's the "old" water already present in the pipe before the pump started working. "New" water that is physically pushed into a pipe by a pump will eventually reach the other end, but not that fast.

Finally, let's talk about measurement of the electric current.
The natural way of measurement of the flow of water in the pipe, as exemplified above, would be amount of water flowing out of a pipe per unit of time.
In our case of electric charge we can do the same - measure the flow by amount of electricity (in coulombs) traveling from one source of electric field to another (with opposite charge) per unit of time.

The unit of measurement of the electric current is ampere, where 1 ampere is the flow of electricity, when 1 coulomb of electricity is moving across the wire within 1 second.
1 A = 1 C / 1 sec.

Recall the definition of a unit volt as a difference in electric potential between points A and B such that moving one coulomb of electric charge between these points requires one joule of work. Therefore,
1 J = 1 V · 1 C
From the definition of ampere above
1 C = 1 A · 1 sec.
Therefore,
1 J = 1 V · 1 A · 1 sec
1 V · 1 A = 1 J / 1 sec
As we know,
1 J / 1 sec = 1 W (watt)
So, electric current of 1 ampere between points with difference of potential 1 volt performs work of 1 watt, that is 1 joule per second.

There is a direct analogy between electricity and mechanics with force analogous to voltage and speed analogous to amperage
Force · Distance = Work
Force · Distance / Time =
= Work / Time = Power
Force · (Distance / Time) =
= Force · Speed = Power
Voltage · Amperage = Power

Let's consider a slightly more complicated example of the electric current.
Assume that at one end of a copper wire we have a source of electric field with negative charge and at another end of this wire we have another source of electric field also with negative charge. Both ends will repel electrons inside a wire. However, if the charges are not equal, the larger one will push stronger, and electrons will move away from it towards the other end of a wire.

The situation with two unequal negative charges is analogous to a water pipe with two pumps of different power pumping water into it from both ends. The stronger pump will overcome the weaker and the water will move from a stronger pump to the weaker.

So, the most important factor in determining the direction of electrons in the wire is the intensity of electric field produced by electric charges. For multiple sources of electric field their vectors of intensity are added. From a general viewpoint, if there is a difference in intensity of electric fields, electrons will travel in the direction defined by a stronger force. In practical situation, when two sources of electricity are applied to two ends of a wire, one positive and one negative, one end attracts electrons and another pushes them away, the flow of electrons will be always from negative to positive charge.

Assume, the intensity of electric field at the end A of a wire is E_A and intensity at the other end B is E_B. If both charges at points A and B are positive or both negative, the vectors E_A and E_B inside a wire are oppositely directed. If the charges are of different sings (which is a typical situation in practical applications of electricity), these vectors are directed the same way.

The force acting on each coulomb of electricity inside a wire is a vector sum of both intensities:
E = E_A + E_B
The work needed to move one coulomb of electricity is, therefore,
W = E·L,
where L is the length of a wire.
This value W represents the difference of electric potentials of the electric field between points A and B, that is the voltage V_AB between them.
The difference in intensity of an electric field corresponds to the non-zero voltage between these points.

If we can maintain the difference in electric field's potential between the two ends of a wire (non-zero voltage between them), the intensity of an electric field will push electrons from one end of a wire to another. This is how direct electric current is maintained.

As electrons move from one end to another, they leave "holes" - spots where they used to be, which are "moving" in the opposite direction. Since we conditionally associate "negative" charge with electrons and "positive" charge with the absence of electrons ("holes"), we can say that the direction of positive charges is opposite to that of negative.

For historical reasons, because electrons were not discovered yet, the direction of positive charges (that is, "holes" that are left, when electrons leave their places) was defined as a direction of the electric current.

The word direct means that the direction of the flow of electrons does not change with time and goes from the end with negative charge to the end with positive charge, which implies that the direction of the electric current (the direction of "holes" left by electrons) is opposite, from positive to negative end. For practical reasons we will not consider the case of the same sign of charges on both ends.

In most practical cases there is a device that separates the electrons from the neutral atoms within some object, thereby producing negative and positive charges on its terminals. If there is some conductor of electricity between these terminals, electrons will move from one terminal to another along this conductor, which constitutes a direct electric current in it.

Unizor - Physics4Teens - Electromagnetism - Electric Field - Capacitors

Notes to a video lecture on http://www.unizor.com

Capacitors

Electric Field of
a Uniformly Charged Disk

Please refer to Problems 4 of "Electric Field", as we will use its results.
The problem there derives a formula of intensity of the electric field produced by an infinitely thin disk of radius R charged with surface density of electricity σ at point P positioned at height h above the center of this disk in case the space around this disk is filled with material with dielectric constant (also known as relative permittivity) ε_r.

The direction of the vector of electric field intensity is along the perpendicular from point P to a charged disk and its magnitude equals to
E(h) =
= [σ/(2ε_r·ε₀)]·[1−1/√1+R²/h² ]

From the above formula for any media filling the space around a charged disk we see that the greater dielectric constant ε_r for the media that fills the space around the charged disk - the smaller intensity of the field around it.

Assume now that our goal is to generate electric charge (excess or deficiency of electrons) and store it somehow. Since electrons are not easily produced from nothing, we should take some electrically neutral object X, separate part of its electrons from the atoms and place them into a different object X₋, which becomes negatively charged, leaving old object positively charged, which we can label now X₊.

For practical reasons objects X₋ and X₊ should be near each other and we should prevent any kind of exchange of electric charge, like a spark, between them, which would negate our efforts to separate negative and positive charges. Considering the proximity of X₋ and X₊, it would be beneficial for avoiding any exchange of the charge between them to have a uniform distribution of charge in each object.

The best configuration of objects X₋ and X₊ that allows approximately uniform distribution of charge in the presence of opposite charge nearby is when both objects are thin flat plates positioned parallel to each other. Other configurations will cause the concentration of charges in places close to the opposite charge and higher intensity of the electric field between them, which might result in a discharging spark. Another configuration might be of two concentric spheres, but it's not very practical.

Consider now two relatively large infinitely thin disks of radius R with opposite charges +Q and −Q positioned parallel to each other, perpendicular to a line connecting their centers and at distance d from each other. Let's measure an intensity of the electric field at any point between these disks on a center line at distance h from positively charged disk (0 ≤ h ≤ d).

The intensity of a combined field of two disks is a vector sum of intensities of all components of this field. The direction of the intensity of both fields is along the center line between them. The probe charge is +1C, so the positively charged disk will repel it, while negatively charged one will attract it. So, we can calculate the magnitude of each field and add them together to get the magnitude of the combined field.

The density of the electric charge for these disks equals to a total charge Q divided by a surface area A. There are two opposite surfaces of each disk, but in case we have two close to each other parallel disks with opposite charges the electric charge of each disk (excess or deficiency of electrons) concentrates on a surface that is close to another disk with an opposite charge. So for each disk the absolute value of charge density is constant that equals to
σ = Q/A = Q/(πR²)

The magnitude of the field intensity from a positively charged disk at distance h from its surface is
E(h) =
= [σ/(2ε_r·ε₀)]·[1−1/√1+R²/h² ]

The magnitude of the field intensity from a negatively charged disk at distance d−h from its surface is E(d−h).

Just as an observation, let's notice that, in case the disks are very large and the distance between them very small, both E(h) and E(d−h) are approximately equal to
E = σ/(2ε_r·ε₀)

Since both vectors of intensity are directed from positive to negative disk (positively charged disk repels the probe charge of +1C positioned in-between the disks, and the negatively charged disk attracts it), the magnitude of the intensity of the combined electric field produced by both disks equals to
E(h) = E(h)+E(d−h)
Expressed in all its details, the formula is quite large and difficult to analyze.

At this point we will do what physicists usually do with a cumbersome formula - assume that in practice certain really small values can be assumed as infinitely small and certain large values to be infinitely large.
Indeed, if h→0 or h→d the assumption above is correct. Representing graphically intensity E as a function of h for R=10 and d=0.1 on a segment 0 ≤ h ≤ d shows hardly visible rise in the middle of a segment with h=d/2.

So, for practical reasons we will assume that the distance between the disks d is very small, while the radius of disks R is very large. Since the point we measure the intensity is between the disks at the distance h from one of them, variables h and d−h can also be assumed as very small.
This assumption leads to consider the values R²/h² and R²/(d−h)² as infinitely large, which result in the following approximate formula for the intensity of a combined field between the disks:
E ≅ σ/(2ε_r·ε₀) + σ/(2ε_r·ε₀) =
= σ/(ε_r·ε₀)
So, approximately, the electric field between the large parallel disks on a small distance from each other is uniform and depends only on the density of electric charge on the disks σ and the dielectric constant of the media between them ε_r.

Let's analyze a process of discharging of electricity between two disks.
Since our purpose is to store the charges and to avoid discharge, we should know how much electricity Q we can store in these two disks before electrons jump from a negatively charged disk to a positively charged because of the force of attraction.

The discharge will be more difficult if the force of attraction between the disks is less. The force of attraction is characterized by the intensity of the field between the disks. Knowing intensity of the field between the disks E, which is the force acting on a unit charge, we can calculate the work needed by a charge of +1C to overcome a distance d between the disks by multiplying the intensity (force) by the distance.

The work needed to discharge +1C, that is the work needed to move +1C of charge from one disk to another (the voltage between the disks) is
V = E·d = σ·d/(ε_r·ε₀)

Let's recall that the purpose of our work is to store as much electric charge in these two disks as possible. But with growing charge Q proportionally grows the density of electricity σ and proportionally grows the intensity of the field and the voltage between the disks.

Let's introduce the new characteristic that defines the ability of our two disk construction, called capacitor, to hold electric charge - capacity C = Q/V.
Defined as such, the capacity of a capacitor described above equals to
C = Q/V = σ·A/[σ·d/(ε_r·ε₀)] =
= A·(ε_r·ε₀)/d

As we see, the capacity of our capacitor depends on three major factors:
(a) the area of the disks (capacity is proportional to this area)
(b) the distance between disks (capacity is inversely proportional to this area)
(c) the dielectric constant of the media between the disks (capacity is proportional to a dielectric constant of the media).

To satisfy the purpose of storing as much electricity in the capacitor as possible, we should increase the area of the disks, decrease the distance between the disks and isolate disks from each other with the media with high dielectric constant.

The disk shape of a capacitor is not really important, as long as it contains two flat parallel shapes on a small distance from each other. The easiest variation from the practical standpoint is two rectangles. Although different shape leads to slightly different results in the value of capacity, the difference is negligible, and it disappears completely when the distance between planes becomes an infinitesimal value. So, the definition of capacity
C = A·(ε_r·ε₀)/d
is quite universal and is widely used as a characteristic of a capacitor.

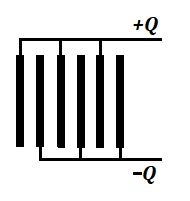
Finally, if we adapt a rectangular form of a capacitor, it's easy to significantly increase the area A by folding or rolling both surfaces together. This technique is actually utilized in manufacturing capacitors of large capacity and it's called parallel connection of capacitors.
In such a way of connecting capacitors the total capacity of an assembly equals to a sum of capacities of individual capacitors
C = C₁+C₂+C₃+C₄+...
This picture depicts an idea to stack smaller individual capacitors to enlarge the area, thus allowing to store more electric charge in a smaller volume.

Unizor - Physics4Teens - Electromagnetism - Electric Field - Voltage

Notes to a video lecture on http://www.unizor.com

Voltage

Recall the concept of the electric field potential.
By definition, the electric field potential is a quantitative characteristic of an electric field, defined for each position in this field, as the amount of work needed to move a probe - positively electrically charged point-object of +1C (one coulomb) - from infinitely remote point in space, where the field does not exist, to this position in the field.

Also recall that in an electric field amount of work to move a charge from one position to another is independent of a trajectory because electrostatic forces are conservative. So, amount of work to move a charge from point A to point B along a straight line between them is the same as if we move along some curve or go from A to an infinitely far point and then return to B.

Electric potential for each point of an electric field fully defines this field. If we know the electric potential at each point of a field, we don't have to know what kind of an object is the source of the field, nor its charge, nor shape in order to understand the movement of any probe object in this field.

To find the amount of work needed to move a charge q from a point in the electric field with a potential V₁ to a point with potential V₂ we can simply multiply the electric charge by the difference of electric potentials between these points:
W = q·(V₂−V₁)
The sign of the resulting value of work W is important. It signifies whether outside force has to perform the work against the forces of the electric field (like forcing a positive charge to go further from the attracting negative charge) or the electric field does the work itself (like forcing a positive charge to go further from the repelling positive charge).

The expression in the parenthesis in the above formula for work W, that signifies the difference in electric potentials between two points in the electric field, is the main component to calculate the work needed to move a charge between these points. This expression has a special name - voltage - in honor of Italian physicist Alessandro Volta.

Since the electric potential is the work performed on the unit charge, the convenient unit of measurement of this potential is the unit of work per unit of charge.

This unit of measurement is called volt (symbol V) and it is defined as such a difference in electric potential between two points in an electric field that one joule of work (1J) is required to move one coulomb of positive charge (+1C) between these points:
1V = 1J/1C

In the electric field produced by an electrically charged point-object with Q amount of electricity the potential at any point depends only on its distance R from the source of the field and equals to k·Q/R. So, the voltage between two points at distances R₁ and R₂ equals to
ΔV = k·Q·(1/R₁ − 1/R₂)

In the electric field produced by an electrically charged infinite plane with density of charge σ the intensity of the field is constant for all points in space and is equal to 2π·k·σ (see Problems 2 of this section). The direction of the force is always perpendicular to the plane. Therefore, moving a probe charge parallel to the plane does not require any work, and the only parameter we have to take into consideration is the height above the plane. The amount of work needed to move a probe charge of +1C from the height H₁ to height H₂ is the product of the force (intensity of the field) by distance (difference in height). Therefore, it equals to
ΔV = 2π·k·σ·(H₂−H₁)

Important Analogy

Producing electric charge by separation of electrons from the neutral atoms can be compared with raising the level of water (or any other liquid) in the tall vertical tube with closed valve at the bottom in the gravitational field of Earth.
Electric charge causes the existence of electric field that is the source of a force on any electrically charged object.
The water raised to a certain height is the source of pressure, which is the force acting on any object at the bottom.
The voltage, which is a difference in electric potential between two points in the electric field is analogous to a difference in potential energy between the water at two different heights.
Connecting positive and negative charges will cause their mutual neutralization, so no electric field and no voltage will be present anymore.
Opening a valve in the vertical tube with water will cause the water to flow down, and no pressure will exist anymore at the bottom of the tube.

This analogy might be useful to understand many facts related to electricity, and it goes much deeper than just about voltage. Electric generators, electric motors, conductors, resistors etc. - all can be to an extent compared with corresponding water-based devices. We will address these concepts, as we progress with the course.

Unizor - Physics4Teens - Electromagnetism - Electric Field - Problems 4

Notes to a video lecture on http://www.unizor.com

Problems 4

Problem A

An infinitesimally thin disk α of radius R is electrically charged with uniform density of electric charge σ (coulombs per square meter). What is the intensity of the electric field produced by this disk at point P positioned at distance h (meters) from its surface on a perpendicular through its center?

Solution
Please refer to Problems 2 of "Electric Field", as we will use its results. The Problem A from Problems 2 is about intensity of the electric field produced by an infinite plane.

Here we will consider a finite electrically charged infinitely thin disk of the radius R instead of an infinite plane as in Problems 2.
Assume, as in Problems 2, the density of electrical charge of this disk is σ and the point we want to measure the intensity of the field is P located above the disk on the perpendicular through its center on height h above it.

Going through exactly the same logic as in Problems 2, dividing our disk into concentric rings, we will come to a formula for intensity produced by an infinitely narrow ring of inner radius r and outer radius r+dr, where r is changing from 0 to R:
dE(h,r) =
= 2π·k·σ·r·dr·h / (h²+r²)^3/2

After substitution
y = 1 + r²/h²
we obtain
dy = 2r·dr/h²
2r·dr = h²·dy
dE(h,y) =
= π·k·σ·dy·h³ / (h²+r²)^3/2=
= π·k·σ·dy / (1+r²/h²)^3/2 =
= π·k·σ·y^−3/2·dy
which is easy to integrate since it's a plain power function.
The limits of integration for r are from 0 to R.
Therefore, the limits of integration for y are from 1 to 1+R²/h².
The indefinite integral of y^−3/2 is −2y^−1/2. Therefore, the total vector of intensity at point P equals to
E(h) =
= −2π·k·σ·[(1+R²/h²)^−1/2−1] =
= 2π·k·σ·[1−(1+R²/h²)^−1/2] =
= 2π·k·σ·[1−1/√1+R²/h² ]

We can rewrite this formula using the permittivity of vacuum ε₀=1/(4π·k) as
E(h) = (σ/2ε₀)·[1−1/√1+R²/h² ]

Analyzing this formula, we see that the intensity of the electric field of a uniformly charged disk of radius R at point above its center on the height h depends on the ratio R/h.
If the height remains the same, but the radius increases to infinity, the formula transforms into the one we obtained in the Problem 2 for infinite charged plane.
If the height h decreases to zero with a fixed radius R, the intensity gradually increases to its maximum value 2π·k·σ, which is the same as for an infinite plane in Problems 2. So, for a small height the uniformly charged disk acts like an infinite plane.
If the height h increases to infinity with a fixed radius R, the intensity gradually decreases to zero.
All conclusions are intuitively obvious.

Another parameter from which the intensity depends is the medium around a charged object. Knowing from a previous lecture about permittivity, we can consider the space around the charged disk to be not only vacuum, but any media with known dialectic constant ε_r.
In this case, instead of Coulomb's constant k, we have to use 1/(4π·ε_r·ε₀) and the formula for intensity looks like this:
E(h) =
= [σ/(2ε_r·ε₀)]·[1−1/√1+R²/h² ]

From the above formula for any media filling the space around a charged disk we see that the greater dielectric constant for this media - the smaller intensity of the field around it.

Unizor - Physics4Teens - Electromagnetism - Electric Field -Permittivity

Notes to a video lecture on http://www.unizor.com

Electric Permittivity

Let's take a closer look at Coulomb's Law
F = k·q_A·q_B / R²
where
F is the magnitude of the force of attraction (in case of opposite charges) or repelling (in case of the same type of charge, positive or negative) in N - newtons
q_A is electric charge of point-object A in C - coulombs
q_B is electric charge of point-object B in C - coulombs
R is the distance between charged objects in m - meters
k is a coefficient of proportionality (Coulomb's constant) equals to 9.0·10⁹ in N·m²/C²

The intuitive explanation of the inverse proportionality of this force to a square of a distance between objects A and B was that the force emitting by an electric point-charge is distributed around it in a radial fashion and, at distance R, should be inversely proportional to an area of a sphere of the radius R.
The area of a sphere of radius R is 4πR². Therefore, it's more natural to express Coulomb's with 4πR² in the denominator. Then it will look like this
F = q_A·q_B / (4π·ε₀·R²)
where
ε₀ is a constant called permittivity of vacuum.
In terms of Coulomb's constant k it is equal to
ε₀ = 1/(4π·k) = 8.85419·10⁻¹²
measured in C²/(N·m²)

In the above definition permittivity is the property of space between the charges to let the force of electric field through. It is analogous to such mechanical properties as resistance, friction, viscosity.

As experiments show, the same electric charges at the same distance but in different environments produce electric fields of different intensities.
Environment matters. In vacuum a specific point-charge at a specific distance produces the field of one intensity, while, positioned inside a sand box, the same charge at the same distance would produce a field of different intensity.

That's why we specifically called ε₀ the permittivity of vacuum, as no other environment was considered. All the experiments described before relate to vacuum as the media where these experiments are conducted. In different environment the force of electric field would differ.

This prompts us to introduce an absolute permittivity ε_a (or simply ε) of any media and its relative permittivity ε_r=ε_a/ε₀.
The relative permittivity of a media is also called its dielectric constant with the value of this dielectric constant for vacuum being equal to 1.
For olive oil the dielectric constant is 3, for silicon its about 11-12, for mineral oil its about 2, for marble - 8, for titanium dioxide - between 86 and 173 etc.

Now the formula for intensity of electric field in a media with relative permittivity ε_r looks like this
F = q_A·q_B / (4π·ε_r·ε₀·R²)
So, generally speaking, when the electric field speads into any media with a dielectric constant ε_r, we should use the coefficient 1 / (4π·ε_r·ε₀) instead of Coulomb's constant k.

The greater the value of the dielectric constant - the stronger it resists to penetration of electric field, so the field is weaker than in vacuum for the same charge and distance. Vacuum is the easiest for the electric field to penetrate.

Also worth noting that the permittivity of any material depends on its temperature and exact chemical composition. This allows, for example, to measure the temperature or humidity of air by measuring its relative permittivity.

Materials with high value of permittivity are used for electrical insulation to prevent the electric field from dissipating around electrical charges.