Lagrangian -
Functional and Variation
To introduce concepts of Functional (a noun, not an adjective) and Variation which happen to be very important mathematical tools of Physics, let's consider the following problem.
Imagine yourself on a river bank at point A.
River banks are two parallel straight lines with distance d between them.
You have a motor boat that can go with some constant speed V relative to water.
The river has a uniform current with known speed v which we assume to be less than the speed of a boat V.
You want to cross a river to get to point B exactly opposite to point A, so segment AB is perpendicular to the river's current.
Problem:
How should you navigate your boat from point A to point B to reduce the time to cross the river to a minimum?
It sounds like a typical problem to find a minimum of a function (to minimize time). But this resemblance is only on a surface.
In Calculus we used to find minimum or maximum of a real function of real argument by differentiating it and checking when its first derivative equals to zero.
In our case the problem is much more complex, because we are not dealing with a function (time to cross the river) whose argument is a real number. The argument to our function (time to cross the river) is a trajectory of a boat from point A to point B.
And what is a trajectory of a boat?
Trajectory is a set of positions of a boat, which is, in its own rights, can be a function of some argument (trajectory can be a function of time, of an angle with segment AB or a distance from line AB in a direction of a river's current).
Trajectory is definitely not a single real number.
In our case the trajectory is determined by two velocity vectors:
velocity vector of a boat V and
velocity vector of a river's current v.
The boat's velocity vector, while having a constant magnitude V can have variable direction depending on navigation scenario.
The current's velocity vector has constant direction along a river bank and constant magnitude v.
So, the time to cross the river is not a function in our traditional meaning as a function of real argument, it's "a function of a function", which is called Functional (a noun, not an adjective).
Examples of Functionals as "functions of functions" are
- definite integral of a real function on some interval,
- maximum or minimum of a real function on some interval, - average value of a real function on some interval,
- length of a curve that represents a graph of a real function on some interval,
etc.
It is impossible to determine minimum or maximum of a Functional by differentiating it by its argument using traditional Calculus, because its argument is not a real number, it's a function (in our case, it's a trajectory as a function of time or some other parameter).
We need new techniques, more advanced Calculus - the Calculus of Variations to accomplish this goal.
We have just introduced two new concepts - a Functional (a noun, not an adjective) as a "a function of a function" and Calculus of Variations as a new technique (similar but more advanced than Calculus) that allows to find minimum or maximum of a Functional.
These concepts are very important and we will devote a few lectures to address these concepts from purely mathematical point before starting using them for problems of Physics.
Before diving into a completely new math techniques, let's mention that in some cases, when solving a problem of finding minimum or maximum of a functional, we can still use classic approach of Calculus.
This can be done if an argument to a functional (a function in its own rights) can be defined by a single parameter. In this case a functional can be viewed as a regular function of that parameter and, as such, can be analyzed by classic Calculus techniques.
Here is an example that is based on a problem above, but with an additional condition about trajectories.
Instead of minimizing the time to cross the river among all possible trajectories, we will consider only a special class of trajectories achieved by a specific scenario of navigation that allows one single real number to define the whole trajectory.
Assume, your navigation strategy is to maintain a constant angle φ between your course and segment AB with positive φ going counterclockwise from segment AB.
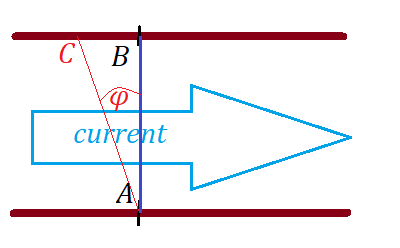
Obviously, angle φ should be in the range (−π/2,π/2).
With an angle φ chosen, a boat will reach the opposite side of a river, but not necessarily at point B, in which case the second segment of a boat's trajectory is to go along the opposite bank of a river up or down a stream to get to point B.
The problem now can be stated as follows.
Find the angle φ to minimize traveling time from A to B.
For this problem a functional (time to travel from A to B), which depends on trajectory from A to B, can be considered as a regular function (time to travel from A to B) with real argument (an angle φ).
Solution for Constant Angle φ:
If you maintain this constant angle φ, you can represent the velocity vector of a boat going across a river before it reaches the opposite bank as a sum of two constant vectors
V = V⊥ + V||
where
V⊥ is a component of the velocity vector directed across the river (perpendicularly to its current) and
V|| is a component of the velocity vector directed along the river (parallel to its current).
The magnitudes of these vectors are
|V⊥| = V·cos(φ)
|V||| = V·sin(φ)
The time for a boat to reach the opposite bank across a river is
T⊥(φ)=d / |V⊥|=d/ [V·cos(φ)]
In addition to moving in a direction perpendicular to a river's current across a river with always positive speed V⊥=V·cos(φ), a boat will move along a river because of two factors: a river's current v and because of its own component V|| of velocity.
The resulting speed of a boat in a direction parallel to a river's current is V·sin(φ)−v, which can be positive, zero or negative.
Therefore, when a boat reaches the opposite side of a river, depending on angle φ, it might deviate from point B up or down the current by the distance
h(φ) = [V·sin(φ)−v]·T⊥(φ)
This expression equals to zero if the point of reaching the other bank coincides with point B, our target.
The condition for this is
V·sin(φ)−v=0 or
sin(φ)=v/V or
φ=arcsin(v/V)=φ0.
So if we choose a course with angle φ0=arcsin(v/V), we will hit point B, and no additional movement will be needed.
Positive h(φ) is related to crossing a river upstream from point B when the angle of navigation φ is greater than φ0 and negative h(φ) signifies that we crossed the river downstream of B when the angle of navigation φ is less than φ0.
In both cases, after crossing a river we will have to travel along a river's bank up or down the current to cover this distance h(φ) to get to point B.
Our intuition might tell that an angle φ0 of direct hit of point B at the moment we reach the opposite side of a river, when h(φ)=0, should give the best time because we do not have to cover additional distance from a point we reached the opposite bank to point B.
It's also important that the actual trajectory of a boat in this case will be a single straight segment - segment AB - the shortest distance between the river banks.
In general, the time to reach the other side of a river depends only on component V⊥ of the boat's velocity and it equals to
T⊥(φ) = d / [V·cos(φ)]
If we choose a course with angle φ=φ0 to reach the opposite side exactly at point B, the following equations take place
sin(φ0)=v/V
V²·sin²(φ0) = v²
V²·cos²(φ0) = V²−v²
V·cos(φ0) = √V²−v²
T⊥(φ0) = d / √V²−v²
This is the total time to get to point B.
If we choose some other angle φ≠φ0, we have to add to the time of crossing a river T⊥(φ) the time to reach point B going up or down a stream along the opposite river bank.
Let's prove now that the course with angle φ=φ0 results in the best travel time from A to B.
The distance from a point where we reach the opposite bank to point B is
h(φ) = [V·sin(φ)−v]·T⊥(φ) =
= [V·sin(φ)−v]·d / [V·cos(φ)]
This distance must be covered by a boat by going down (if h(φ) is positive) or up (if h(φ) is negative) the river's current.
Let's consider these cases separately.
Case h(φ) is positive
This is the case of angle φ is greater than φ0.
Obviously, the timing to reach point B in this case will be worse than if φ=φ0 with h(φ0)=0.
First of all, with a greater than φ0 angle φ the river crossing with speed V⊥(φ)=V·cos(φ) will take longer than with speed V⊥(φ0)=V·cos(φ0) because cos() monotonically decreases for angles from 0 to π/2.
Secondly, in addition to this time, we have to go downstream to reach point B.
So, we should not increase the course angle above φ0.
Case h(φ) ≤ 0 because φ ≤ φ0
This scenario is not so obvious because crossing the river with angle φ smaller than φ0 but greater than 0 takes less time than with angle φ0.
But it adds an extra segment to go upstream after a river is crossed.
The extra distance h(φ) is negative because V·sin(φ is less than v, which allows a current to carry a boat below point B.
Since the point of crossing the river is below point B, the distance |h(φ)| should be covered by going upstream with speed V−v, which will take time
Th(φ) = |h(φ)| / (V−v)
Using the same expression for h(φ) but reversing its sign to deal with its absolute value, we get the additional time to reach point B after crossing a river
| Th(φ) = |
|
| T(φ)= |
|
| T'(φ) = |
|
Therefore, its minimum is when its argument is the largest, that is if φ=φ0, h=0 and the time to get to point B is
TAB = T⊥ = d / [V·cos(φ)]
So, the answer to our simplified problem, when we managed to solve it using the classic methodology, is to choose the course of navigation from A to B at angle φ0=arcsin(v/V).
The minimum time of traveling is TAB=d / [V·cos(φ)]
As you see, in some cases, when a set of functions that are arguments to a functional can be parameterized by a single real value (like with an angle φ in the above problem), optimization problems can be solved using classic Calculus.
The subject of a few future lectures is Calculus of Variations that allows to solve problems of optimization in more complicated cases, when parameterization of arguments to a functional is not possible.

 As you see, for any abscissa x the ordinate of an ellipse is smaller than the ordinate of a circle by the same factor b/a.
As you see, for any abscissa x the ordinate of an ellipse is smaller than the ordinate of a circle by the same factor b/a. The area of a triangle formed by two vectors
The area of a triangle formed by two vectors 
