AC Power
Power is a rate of work performed by some source of energy (like electric current) per unit of time. More precisely, it's a derivative of work performed by a source of energy, as a function of time, by time.
As we know from the properties of a direct electrical current, its power is
P = U·I = I²R = U²/R
where U is the voltage around a resistor of resistance R and I is the electric current going through this resistor.
All values in the above expression are constant for direct current.
Alternating current presents a problem of having the voltage and the current to be variable and dependent not only on the resistors, but also on the presence of inductors and capacitors in the circuit.
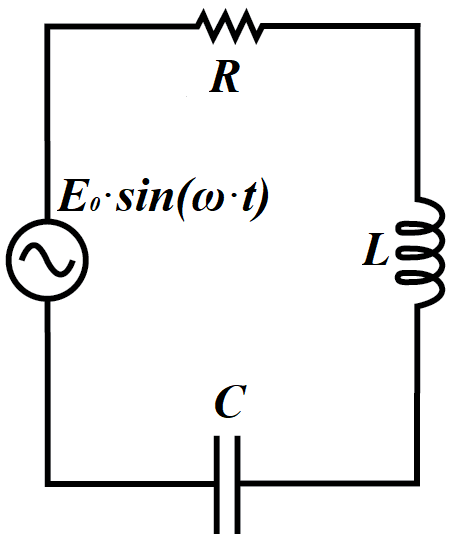
As described in the previous lecture, the alternating current in the circuit of a resistor, an inductor and a capacitor connected in a series to a generator of sinusoidal EMF equals to
I(t) = (E0 /Z)·sin(ωt+φ) =
= I0·sin(ωt+φ)
where impedance Z=√(XC−XL)²+R²,
tan(φ)=(XC−XL)/R.
Having expressions for generated EMF E(t)=E0·sin(ωt) and electric current in a circuit I(t)=I0·sin(ωt+φ), we can find an instantaneous power
P(t) = E(t)·I(t) =
= E0·I0·sin(ωt)·sin(ωt+φ)
When people talk about voltage or amperage in the AC circuit, they understand that these characteristics are variable and, to be more practical, they use effective voltage
W[0,T] = Eeff · Ieff · T
Adding an inductor and a capacitor brings some complication because of a phase difference between EMF and a current. To express the power consumed by an AC circuit that includes a resistor, an inductor and a capacitor in terms of effective voltage and effective amperage, let's find the work performed by an electric current during a period of oscillation in terms of Eeff and Ieff and divide it by this period. The result would be an average power consumed by a circuit per time of one oscillation that we will call the effective power of a circuit.
The period of one oscillation with angular speed ω is T=2π/ω.
The instantaneous power consumption by a circuit is
P(t) = E(t)·I(t) =
= E0·sin(ωt)·I0·sin(ωt+φ)
The energy consumed by a circuit during one period of oscillation T=2π/ω equals to
W[0,T] = ∫[0,T]P(t)·dt
where
P(t)=E0·sin(ωt)·I0·sin(ωt+φ)
We can simplify the product of two trigonometric functions to make it easier to integrate:
sin(x)·sin(y) =
= (1/2)·[cos(x−y)−cos(x+y)]
Using this for x=ωt and y=ωt+φ, we obtain
sin(ωt)·sin(ωt+φ) =
= (1/2)·[cos(φ)−cos(2ωt+φ)]
To find the power consumption during one period of oscillation T, we have to calculate the following integral
W[0,T] = ∫[0,T]P(t)·dt
where period T=2π/ω and
P(t) = E0·I0·
·(1/2)·[cos(φ)−cos(2ωt+φ)]
This integral can be expressed as a difference of two integrals
∫[0,T]E0·I0·(1/2)·cos(φ)·dt
which, considering cos(φ) is a constant for a given circuit, is equal to
E0·I0·(1/2)·cos(φ)·T =
= E0·I0·(1/2)·cos(φ)·2π/ω
and
∫[0,T]E0·I0·(1/2)·cos(2ωt+φ)·dt
which is equal to zero because integral of a periodical function cos(x) over any argument interval that equals to one or more periods equals to zero.
The same can be proven analytically
∫[0,T]cos(2ωt+φ)·dt =
= sin(2ωt+φ)/(2ω)|[0,T] =
= sin(2ω·2π/ω+φ)/(2ω) −
− sin(φ)/(2ω) =
= [sin(4π+φ)−sin(φ)]/(2ω) = 0
Hence, the energy consumed by a circuit during one period of oscillation equals to
W[0,T] = E0·I0·(1/2)·cos(φ)·2π/ω
The average power consumption, that is the average rate of consuming energy that we will call effective power, equals to this amount of energy divided by time, during which it was consumed - one period of oscillation T=2π/ω:
Peff = W[0,T]
= E0·I0·(1/2)·cos(φ)
Since
Peff = Eeff·Ieff·cos(φ)
where a phase shift φ depends on resistance and reactances of a circuit as follows
tan(φ) = (XC − XL) /R
XC = 1/(ωC) - capacitive reactance,
XL = ωL - inductive reactance,
R - resistance.
The above formula is derived for RLC-circuit that contains a resistor or resistance R, a capacitor of capacitance C and an inductor of inductance L
Let's analyze different circuits and their effective power consumption rate.
R-Circuit
R-circuit contains only a resistor. Therefore, both reactances XC and XL are zero and phase shift φ is zero as well. Since cos(0)=1, the effective power for this R-circuit is
Peff = Eeff·Ieff
which fully corresponds to a power for a circuit with a direct current running through it.
RC-Circuit
RC-circuit contains a resistor and a capacitor in a series. Reactance XL is zero.
Peff = Eeff·Ieff·cos(φ)
where tan(φ) = XC /R
RL-Circuit
RC-circuit contains a resistor and an inductor in a series. Reactance XC is zero.
Peff = Eeff·Ieff·cos(φ)
where tan(φ) = −XL /R
The negative values of tan(φ) is not important since function cos(φ) is even and cos(φ)=cos(−φ).
Interestingly, if our circuit contains a resistor, but a capacitor and an inductor are in resonance, that is XC=XL, the phase shift will be equal to zero, as if only a resistor is present in a circuit.
L-, C- and LC-Circuits
If no resistor is present in the circuit (assuming the resistance of wiring is zero), the denominator in the expression
tan(φ) = (XC − XL) /R
is equal to zero.
Therefore, the phase shift is φ=π/2=90°, cos(π/2)=0 and the power consumption is zero. So, only resistors contribute to a power consumption. Inductors and capacitors are not consuming any energy, they only shift the current phase relatively to a generated EMF. And, if an inductor and a capacitor are in resonance, there is no phase shift, they neutralize each other.