Unizor - Physics4Teens - Electromagnetism - Magnetism and Electric Curre...

Notes to a video lecture on http://www.unizor.com



Two Currents - Problems 1



IMPORTANT NOTES



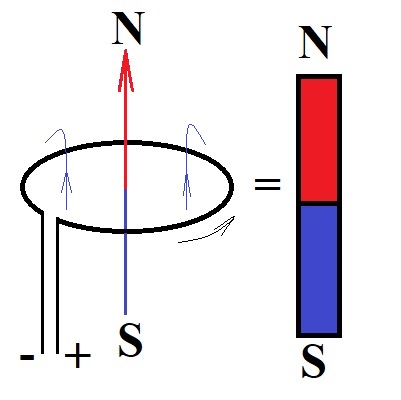
As we know from a previous lecture, the magnetic field force lines
around a long thin straight line wire with electric current running
through it are circular in planes perpendicular to a wire and centered
at the points of the wire.





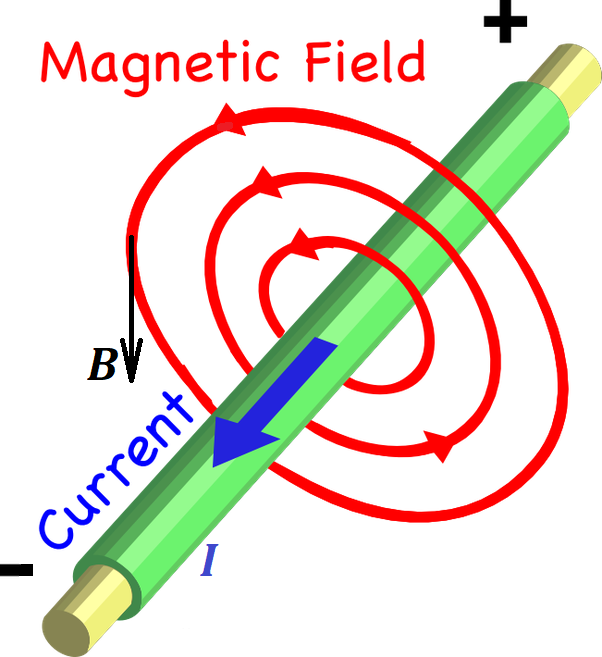
These lines are attributed a direction that can be determined using the rule of the right hand or Maxwell's corkscrew rule.



The rule of the right hand states that, if you wrap your right
hand around a wire such that your thumb points to a direction of an
electric current in the wire, which is, by definition, from positive to
negative, then your fingers will point to a direction of the magnetic
field lines. This direction is the direction of any tangential to a line
vector of force.



The corkscrew rule states that, if we imagine a corked bottle
along the wire such that the direction of an electric current enters the
bottle through a cork, to open the bottle we need to rotate the regular
cork opener in the direction of the magnetic lines around the wire.



The magnitude of the intensity of a magnetic field (a vector of force) depends on the electric current's amperage I and the distance R to the wire as follows

B = μ₀I/(2π·R)

where μ₀ is a constant called permeability of vacuum.



The direction of this force vector at any point of space around a wire
is always in the same plane as a circular magnetic line going through
the same point and is tangential to this magnetic line.

The direction of the vector corresponds to the direction of the magnetic line.



Problem 1A

Two ideally long and thin wires are positioned in space with Cartesian coordinates.

One goes through point A(0,0,a) on Z-axis (a > 0) parallel to X-axis and carries an electric current of amperage I in the positive direction of X-axis.

Another wire goes through point B(0,0,−a) on Z-axis parallel to Y-axis and carries an electric current of the same amperage I in the positive direction of Y-axis.

Determine the X-, Y- and Z-components and magnitude of the vector of magnetic field intensity at the origin of coordinates (0,0,0).



Solution



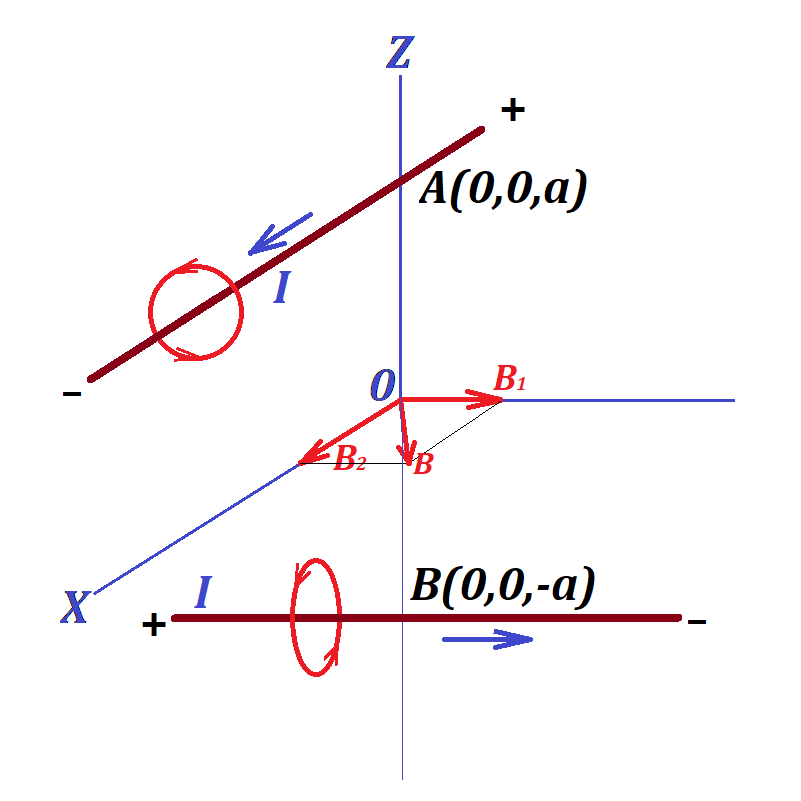
The magnetic field at point (0,0,0) is a combination of two fields - one with intensity vector B₁, the source in the first wire that carries electric charge I parallel to X-axis, from which the origin of coordinates is at distance a, and another with intensity vector B₂, the source in the second wire that carries electric current I parallel to Y-axis, from which the origin of coordinates is at distance a.

The resulting field intensity vector is a vector sum of vectors B₁ and B₂.



The first magnetic field has its force lines forming a cylindrical
surface with an axis being the first wire parallel to X-axis. At point (0,0,0) the direction of this magnetic field intensity vector is perpendicular to a radius from the first wire towards point (0,0,0), that is along the Y-axis towards its positive direction.

Considering the values of electric current I and the distance to the source (the first wire) equaled to a, the magnitude of this vector is

|B₁| = μ₀·I/(2π·a)

So, this vector in Cartesian coordinates is

{0; μ₀·I/(2π·a); 0}



The second magnetic field has its force lines forming a cylindrical
surface with an axis being the second wire parallel to Y-axis. At point (0,0,0) the direction of this magnetic field intensity vector is perpendicular to a radius from the second wire towards point (0,0,0), that is along the X-axis towards its positive direction.

Considering the values of electric current I and the distance to the source (the second wire) equaled to a, the magnitude of this vector is

|B₂| = μ₀·I/(2π·a)

So, this vector in Cartesian coordinates is

{μ₀·I/(2π·a); 0; 0}



Therefore, the combined vector of magnetic field intensity has its three coordinates

{μ₀·I/(2π·a); μ₀·I/(2π·a); 0}



The magnitude of this vector is

μ₀·I·√2/(2π·a)



Problem 1B

Two ideally long and thin wires are positioned in space parallel to Z-axis.

One goes through point A(a,0,0) (a > 0) and carries an electric current of amperage I₁ in the negative direction of the Z-axis.

Another wire goes through point B(0,b,0) (b > 0) and carries an electric current of amperage I₂ in the positive direction of the Z-axis.

Determine the X-, Y- and Z-components and magnitude of the vector of magnetic field intensity at the origin of coordinates (0,0,0).



Solution



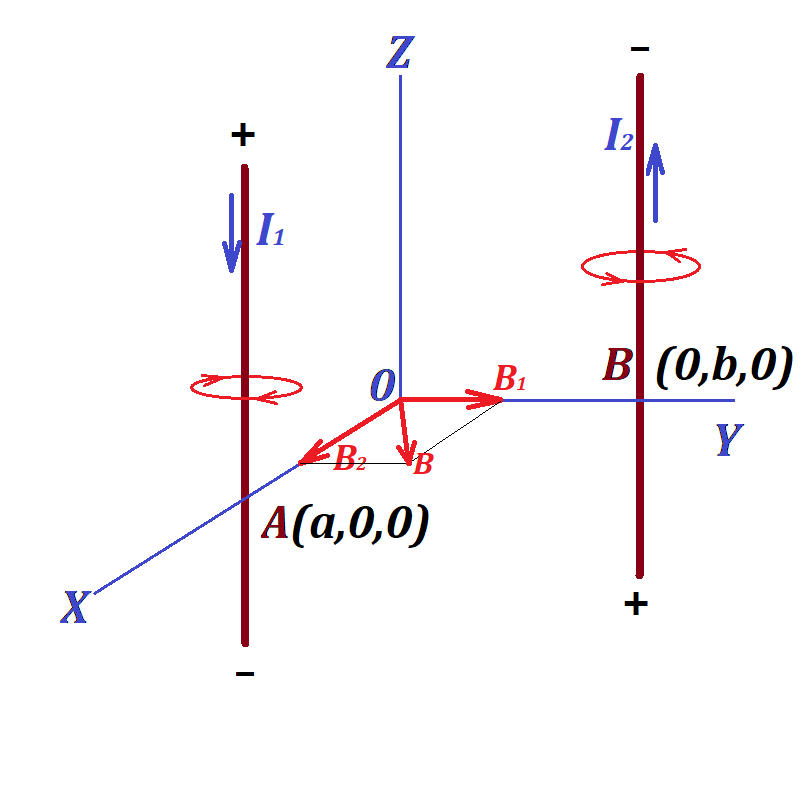
The magnetic field at point (0,0,0) is a combination of two fields - one with intensity vector B₁, the source in the first wire that carries electric charge I₁, from which the origin of coordinates is at distance a, and another with intensity vector B₂, the source in the second wire that carries electric current I₂, from which the origin of coordinates is at distance b.

The resulting field intensity vector is a vector sum of vectors B₁ and B₂.



The Z-coordinate of both vectors is zero.



The first magnetic field has its force lines forming a cylindrical surface with an axis being the first wire. At point (0,0,0) the direction of this magnetic field intensity vector is perpendicular to a radius from the first wire towards point (0,0,0), that is along the Y-axis towards its positive direction.

Considering the values of electric current I₁ and the distance to the source (the first wire) equaled to a, the magnitude of this vector is

|B₁| = μ₀·I₁/(2π·a)

So, this vector in Cartesian coordinates is

{0; μ₀·I₁/(2π·a); 0}



The second magnetic field has its force lines forming a cylindrical surface with an axis being the second wire. At point (0,0,0) the direction of this magnetic field intensity vector is perpendicular to a radius from the second wire towards point (0,0,0), that is along the X-axis towards its positive direction.

Considering the values of electric current I₂ and the distance to the source (the second wire) equaled to b, the magnitude of this vector is

|B₂| = μ₀·I₂/(2π·b)

So, this vector in Cartesian coordinates is

{μ₀·I₂/(2π·b); 0; 0}



Therefore, the combined vector of magnetic field intensity has its three coordinates

{μ₀·I₂/(2π·b); μ₀·I₁/(2π·a); 0}



The magnitude of this vector is

[μ₀/(2π)]√(I₁/a)²+(I₂/b)²

Unizor - Physics4Teens - Electromagnetism - Magnetism and Electric Current

Notes to a video lecture on http://www.unizor.com



Magnetism of Straight Line Current



Magnetic properties of permanent magnets are attributed to parallel
orientation of all axes of rotation of electrons around corresponding
nuclei and the same direction of this rotation.



Consider an Ampere model of magnetism that we have addressed in one of
the previous lectures and, in particular, all electrons rotating in the
same plane.

If all electrons rotate in the same direction within the same plane
around parallel axes, electrons moving near each other are moving in
opposite directions and neutralize each other, as if there is no current
there at all.



So, within every plane perpendicular to the North-South axis of a magnet
all inner currents are neutralized, and the only really present current
is around the outer boundary of a magnet.



This makes the magnetic properties of permanent magnet equivalent to
properties of an electric current in a loop. The flow of electrons,
constituting this electric current, occurs within one plane with a
perpendicular to this plane making the North-South line of this
artificially made magnet.





Simple experiment with iron filings confirms the similarities of
magnetic properties of permanent magnet and a loop of wire with electric
current running through it.





In the previous lectures we described the Lorentz force that acts on the
electric current in the magnetic field of a permanent magnet. Now we
will use the electric current as the source of the magnetic field and
will talk about the properties of this magnetic field in relation to
electric characteristics of the current.



First of all, we will switch from an electric current in a loop to a straight line current.

Consider the magnetic field lines around the wire carrying the electric
current in a loop. Inside a loop they go in the direction from the South
pole towards the North along the axis, then circle around the wire from
the North pole back to the South.

The round shape of a wire causes the polarization of the magnetic field.
Polarity is determined by the high density of the magnetic field lines
inside the loop, all pointing to the North, while the opposite direction
of the lines outside the wire loop is less dense, representing a weaker
magnetic field.



Now let's open up a loop into a straight line electric current.

Magnetic field will not disappear and magnetic field lines will still go
around the wire that carries an electric current, just more
symmetrically than in case of a wire in a loop.

Simple experiment with iron filings confirms the circular shape of
magnetic field lines around a straight line wire carrying an electric
current.





The following picture represents a straight line wire carrying the electric current and magnetic field lines around it.



The current in the wire causes the magnetic field to be formed around it.

The magnetic field lines are now completely symmetrical relative to the
wire, thus the magnetic field has no polarity. All lines are perfectly
circular, each forms a circle of certain radius around a wire, lying in
the plane perpendicular to the wire and representing the points of the
same strength of the intensity vector of the magnetic field.



Let's assume that our wire is ideally straight, infinitely long, and infinitesimally thin.

Our task is to relate the electric current running through it with the intensity of the magnetic field B around it at distance R from the wire.



The intensity of the magnetic field B is a vector, whose
magnitude we want to determine. The direction of this vector is always
tangential to the circular magnetic line lying in the plane
perpendicular to the wire and going through a point where we want to
measure this magnetic field intensity and, therefore, always
perpendicular to the wire.



From considerations of symmetry, the distance R should be
the only variable needed to characterize a point in space around the
wire, where we want to determine the intensity of the magnetic field.



Since the magnetism of an electric current running through a straight
wire depends on existence of the current in a wire, it's reasonable to
assume that the more electrons participate in the current (that is, the
greater amount of electricity goes through a wire per unit of time, that
is, the greater amperage of an electric current I) - the stronger magnetic effect it causes. So, the intensity of a magnetic field B around a wire with electric current I running through it should be proportional to the amperage of the electric current in a wire:

B ∝ I



If we consider a field, including a magnetic field, as some form of
energy, emitting by a source of this field and spreading into space all
around this source with certain speed, at any given moment of time it
reaches new "frontier" and spreads over this surface of equal timing
(this is not a generally used terminology, but is appropriate to better
understand the concept of a field). Obviously, the farther we are from a
source - the greater "frontier" area is covered by a field and less of a
field energy falls on a unit of area of this surface.

Hence, the field intensity, which can be viewed as amount of energy
falling on a unit of area per unit of time should diminish as the
distance from the source of a field is increasing because the area of a
surface of equal timing increases with time.



These considerations were a basis for deriving the intensity of an
electrostatic field of a point charge as being inversely proportional to
a square of a distance from this point charge and related to the fact
that all points at a distance R from a source of a filed form a sphere and the area of a sphere of radius R around a source of a field is 4πR².
The same amount of energy going through a sphere of one radius goes
through a sphere of a radius twice as big and, therefore, "covers" the
area four times bigger.



Let's examine the magnetic field of a straight line current using the same logic.

In this case the field source is a straight line. All points on the same
distance from it form a cylinder. The side area of a cylinder of a
radius R and height H is 2πR·H, that is proportional to a radius R.
The height is not important in our case since we assumed that the wire
carrying the electric current is infinite, but the factor 2πR must be in the denominator of a the formula for intensity of a magnetic field of a straight line electric current.



So, we have logically came to a conclusion of proportionality of the
intensity of a magnetic field to the amperage of the current and inverse
proportionality to the distance from the wire:

B ∝ I/(2πR)



Coefficient of proportionality in this formula is called the permeability of free space and is denoted μ₀. So, the final formula for intensity of a magnetic field of a straight wire carrying electric current I at a distance R from a wire is:

B = μ₀I/(2πR)

The value of the permeability of free space constant depends on the
units of measurement and in SI units, according to the above formula,
it's supposed to be measured in

T·m/A = N·m/(A·m·A) = N/A²

Its value is, approximately,

μ₀ ≅ 4π·10⁻⁷ N/A²

Unizor - Physics4Teens - Electromagnetism - Magnetic Field - Magnetic Fi...

Notes to a video lecture on http://www.unizor.com



Magnetic Field Lines



Magnetic field is a force field, which means that there is
a force, acting on a probe object positioned at a distance from the
source of this field, and a force is a vector that has a direction and a magnitude.

Let's examine this force and attempt to determine a direction and a
magnitude of vectors of force at different locations around a magnet,
acting as a source of a field.



Our first complication is a kind of a magnet at the source of a magnetic
field. Different shapes (bar, ring, horseshoe etc.) result in
differently arranged fields.

Recall that we model the permanent magnet as a set of electrons
circulating around parallel axes in the same direction on parallel
planes. Each of these rotating electrons we considered as a tiny bar
magnet with two poles located on an axis on two opposite sides of a
plane of rotation. This construction is called a magnetic dipole.

This magnetic dipole is the most elementary magnet possible, and we can use it in our study of the properties of a magnetic field.



Bar magnet would be the best choice for a source of a magnetic field for
our study, since it closely resembles each elementary magnetic dipole
created by one rotating electron.



The next decision we have to make is the shape of a probe object. It is
important since different shapes would behave differently in the same
magnetic field.

Here, again, we choose the bar magnet, as the simplest. Note that a
magnet is not a point-object because it has two poles. Therefore, we
have to consider two types of its motion - translational motion of its
center and rotation around its midpoint.



In the previous lecture we presented a two-dimensional picture of iron
filings dropped around a bar magnet. Schematically, it's represented as



Lines around this magnet represent the magnetic field lines,
along which the filings link to each other, and the direction of the
compass needle, if positioned at any point in this magnetic field.



The designation of which pole of a magnet is North and which is South is
traditional - if hanging freely, North pole of a permanent magnet is
the one pointing to geographical North of the Earth. After one magnet's
poles are defined, all other magnets' poles can be determined using
their interaction with previously defined, according to the rule
"similar repel, different attract".

By the way, it means that the magnetic pole of the Earth that is close
to its geographical North pole is, technically speaking, the South
magnetic pole of the Earth. So, when someone says "North magnetic pole
of the Earth", it, most likely, means "Magnetic pole of the Earth that
is close to its geographical North pole". Not always, though, so it
might lead to confusion.



Arrows on each line from North pole of a magnet towards its South pole
are the traditional definition of the magnetic force direction. It's
just the agreement among people similar to an agreement about the
definition of the flow of electricity from positive terminal of the
source of electricity (where, in reality, there is a deficiency of
electrons) to its negative terminal (with excess of electrons), in spite
of the real moving of electrons in the opposite direction.



Another important quality of these magnetic field lines is that,
if the source of a magnetic field (a bar magnet on the picture above) is
fixed on a flat surface and another very small and light probe magnet
could freely move without friction in the magnetic field on that
surface, its center would move along the magnetic field lines in
the direction of the arrows on the picture above, always oriented
tangential to a magnetic line it's moving along, pointing its North pole
towards the South pole of a magnet that is the source of the magnetic
field.



Magnetic field lines never cross, as they represent the
trajectories. If they cross at any point, the probe magnet would have
ambiguous dynamics at this point.



The density of the magnetic field lines visually represents the
strength of the magnetic forces at each point. The lines close to the
poles of a magnet are the most dense, as the field is stronger there.



Let's position our probe bar magnet on any line around a source of this
magnetic field. If we let it turn freely, as if this probe magnet is an
arrow of a compass, it will align along the tangential to a magnetic field line it is on.



The North pole of a probe object in this position will point towards the
South pole of a bar magnet in the center of the field and the South
pole of a probe magnet will point towards the North pole of a center
magnet.



Two attracting and two repelling forces from two poles of a center magnet, acting on a probe object, represent the torque that turns the probe magnet and holds it in a position along the magnetic field line.

The pole of a center magnet that is closer to a probe object forces the
probe object to turn the opposite pole towards it to a greater degree.



Obviously, there is a resultant force that ultimately moves the center of a probe object closer to a center magnet.



Also, in a special case of a probe object positioned exactly on the
continuation of the North-South line between the poles of the center
magnet both forces from two poles of a center magnet act along this same
line and can be added easily.



The above considerations are related to a direction of the forces acting on a probe magnet in the magnetic field of a bar magnet.

The magnitude of these forces is a more involved subject and is
related to techniques of measurement of the strength of a magnetic field
at different points. This will be a subject of the next topic.

Unizor - Physics4Teens - Electromagnetism - Magnetic Field - Problems 1

Notes to a video lecture on http://www.unizor.com



Magnetism - Lorentz Force - Problems 1



Problem 1a

Consider the experiment pictured below.



A copper wire (yellow) of resistance R is connected to a battery with voltage U and is swinging on two connecting wires (green) in a magnetic field of a permanent magnet.

All green connections are assumed light and their weight can be ignored.
Also ignored should be their electric resistance. Assume the uniformity
of the magnetic field of a magnet with magnetic field lines directed
vertically and perpendicularly to a copper wire.

The mass of a copper wire is M and its length is L.

The experiment is conducted in the gravitational field with a free fall acceleration g.

The magnetic field exerts the Lorentz force onto a wire pushing it
horizontally out from the field space, so green vertical connectors to a
copper wire make angle φ with vertical.

What is the intensity of a magnetic field B?



Solution



T·cos(φ) = M·g

T = M·g/cos(φ)

F = T·sin(φ) = M·g·tan(φ)

I = U/R

F = I·L·B = U·L·B/R

M·g·tan(φ) = U·L·B/R

B = M·R·g·tan(φ)/(U·L)



Problem 1b

An electric point-charge q travels with a speed v along a wire of length L.

What is the value of the equivalent direct electric current I in the wire that moves the same amount of electricity per unit of time?

What is the Lorentz force exerted onto a charge q, if it moves in a uniform magnetic field of intensity B perpendicularly to the field lines with a speed v.



Solution

Let T be the time of traveling from the beginning to the end of a wire.

T = L/v

I = q/T = q·v/L

F = I·L·B = q·v·B

Notice, the Lorentz force onto a wire in case of only a point-charge
running through it does not depend on the length of a wire, as it is
applied only locally to a point-charge, not an entire wire. Would be the
same if a particle travels in vacuum with a magnetic field present.



Problem 1c

An electric point-charge q of mass m enters a uniform magnetic field of intensity B perpendicularly to the field lines with a speed v.



Suggest some reasoning (rigorous proof is difficult) that the trajectory
of this charge should be a circle and determine the radius of this
circle.



Solution

The Lorentz force exerted on a point-charge q, moving with speed v perpendicularly to force lines of a permanent magnetic field of intensity B, is directed always perpendicularly to a trajectory of a charge and equals to F=q·v·B (see previous problem).



Since the Lorentz force is always perpendicular to trajectory, the linear speed v of a point-charge remains constant, while its direction always curves toward the direction of the force. Constant linear speed v
means that the magnitude of the Lorentz force is also constant and only
direction changes to be perpendicular to a trajectory of a charge.



According to the Newton's Second Law, this force causes acceleration a=F/m,
which is a vector of constant magnitude, since the Lorentz force has
constant magnitude and always perpendicular to a trajectory, since the
force causing this acceleration is always perpendicular to a trajectory.

So, the charge moves along a trajectory with constant linear speed and
constant acceleration always directed perpendicularly to a trajectory.



Every smooth curve at any point on an infinitesimal segment around this
point can be approximated by a small circular arc of some radius (radius of curvature) with a center at some point (center of curvature). If a curve of a trajectory on an infinitesimal segment is approximated by a circle of some radius R, the relationship between a radius, linear speed and acceleration towards a center of this circle (centripetal acceleration), according to kinematics of rotational motion, is

a = v²/R

Therefore, R = v²/a



Since v and a are constant, the radius of a curvature R
is constant, which is a good reason towards locally circular character
of the motion of a charge. It remains to be proven that the center of
the locally circular motion does not change its location, but this is a
more difficult task, which we will omit.

Hence,

R = v²/a = m·v²/F =

= m·v²/q·v·B = m·v/q·B

Unizor - Physics4Teens - Electromagnetism - Magnetic Field - Lorentz Force

Notes to a video lecture on http://www.unizor.com



Magnetism - Lorentz Force



In this lecture we will look at the interaction between an electric current and a magnetic field.



We start with an analogy between magnetic properties of a wire loop with
electric current running through it and those of a permanent magnet.
This have been explained in the previous session from the position of Ampere model of magnetism.

The picture below illustrates this analogy.



The wire loop with electric current running through it (thin black arrow
from left to right) creates a magnetic field around it. The lines of
this magnetic field (thin dark blue arrows from bottom up) go through
the wire loop and around it, closing on themselves, forming their own
loops. Inside the wire loop the direction of magnetic lines is from
South pole to North, while outside the wire loop they go from North pole
to South. Those magnetic filed line loops that are on the same distance
from the wire make up a tubular surface (a torus) around the wire.



This wire loop with electric current running through it and a magnetic
field around it would behave like a magnet, like a compass arrow, for
example.



In particular, positioned inside some external magnetic field, like in
the magnetic field of the Earth, and allowed to turn free, it will
orient itself in such a way that its North pole will point to a South
pole of an external magnetic field, which, in case of the magnetic field
of the Earth, is located not far from its geographical North pole.



It should be noted that circular form of a wire loop is not essential.
If it's rectangular, the magnetic behavior will be the same. It is,
actually, more convenient to work with a rectangular frame to illustrate
the interaction of magnetic field and electric current.



Let's start the experiment with a rectangular wire loop, that can rotate
around a vertical axis in the external magnetic field. Position it such
that one vertical segment of a wire is close to one pole of an external
magnet, while an opposite side is close to another pole. Let the
electric current run through it.



If this wire frame with electric current running through it is allowed
to rotate around a vertical axis, it will reorient itself with its North
pole directed to the left towards the South pole of an external magnet,
and its South pole directed to the right towards the North pole of an
external magnet, as shown on a picture below. The distance from the
North pole of an external magnetic field to both vertical sides of a
wire will be the same. Same about the South pole of the external
magnetic field.



This turn of a wire is, obviously, the result of forces of interaction
between external magnetic field and electric current with its own
magnetic field around it.



Consider the same two states of a wire (before and after the turn) viewed from above.

The initial position of a wire, viewed from above with rotating forces acting on it (blue arrows) is



Magnetic field lines of a wire with electric current running through it
are oriented along vertical direction on this picture, while the
magnetic field lines of an external magnetic field are horizontal.



As in the case of a compass arrow, aligning itself along the magnetic
field lines of the Earth, the external magnetic field forces, acting on
the magnetic field of a wire (blue arrows), will turn the wire to orient
its magnetic field lines along the magnetic field lines of an external
magnetic field, as shown on the following picture





At this final position external magnetic field forces (blue arrows) are
balancing each other and the rotation of a wire (after a short wobbling)
will stop.



Let's analyze the forces acting on a wire to turn it this way.

For this we don't really need a wire loop of any shape, it's sufficient
to have a linear wire with electric current running through it
positioned in an external magnetic field.



If we open up a wire loop into a straight line with electric current
running through it, the magnetic field around a wire will still exist,
and its lines will be positioned around a wire. Magnetic lines located
on the same distance from a wire with electric current will form a
cylinder with the line of electric current being its axis.



The picture below illustrates the force acting on a straight wire with
electric current running through it (straight black line) and its own
magnetic field (thin orange ovals around a wire) when it's positioned in
the external magnetic field. In this case the lines of the external
magnetic field (light blue arrows going left to right) are perpendicular
to the wire and the direction of the force is perpendicular to both,
the direction of the current in the wire and the direction of the
magnetic lines of the external magnetic field.



The direction of the force can be determined by the "rule of the right
hand", which states that, if the magnetic lines of the external magnetic
field are perpendicularly entering the right hand, while the thumb is
directed towards the electric current in the wire, fingers will show the
direction of force.

A different formulation of the "right hand rule" that results in the
same configuration states that, if magnetic field lines of the external
magnetic field are positioned along the fingers in the direction pointed
by them and the electric current in the wire is running in the
direction of the thumb, then the force exerted by the magnetic field on
the wire is perpendicular to the hand going outside of it.



When the wire has a rectangular shape, as on the picture in the
beginning of this lecture, two side of a rectangle are perpendicular to
the magnetic lines of an external magnetic field. The current in these
wire segments is running in opposite directions. As a result, the force
of magnetic field pushes these sides of a wire in opposite directions,
and the wire will turn until these two opposite forces balance each
other.



The force of an external magnetic field exerted on the wire with electric current running through it is called Lorentz force.



All the above considerations on interaction between an external magnetic field and an electric current are of qualitative character.

Let's address quantitative character of this interaction.



For starter, we will reduce our interest only to a case of a uniform
magnetic field and an infinitesimally thin straight wire running
perpendicularly to the magnetic field lines, like on the picture above.



It is reasonable to assume that the force exerted by a magnetic field acts on each moving electron within a wire.



Considering the force does not exist, if there is no electric current in
a wire (electrons are not moving), but can be observed only when there
is an electric current in a wire, another reasonable assumption is that
the force depends on the speed of moving electrons, which can be
measured as amperage of the electric current.



Experiment shows that the force is proportional to an amperage,
which can be intuitively explained by the idea that the higher the
amperage - the greater "number" of magnetic field lines of an external
magnetic field, crossed by electrons per unit of time, and each such
crossing results in certain incremental increase in the force exerted by
a field.



One more natural assumption is that the longer the wire - the
proportionally greater is the force exerted on it by a magnetic field.
This also is related to the above mentioned idea of a magnetic field
exerting a force on each electron crossing its magnetic field lines.



As a result, we come to a conclusion that the force is proportional to a product of electric current and the length of a wire:

F = b·I·L

where

b is a coefficient of proportionality that characterizes the strength of an external magnetic field,

I is the amperage of an electric current running through a wire,

L is the length of a wire.



What's interesting about this formula is that it allows to establish the
units of measurement of the strength of a magnetic field in terms of
units of measurement of force (F), electric current (I) and length (L).



DEFINITION

A uniform magnetic field that exerts a strength of (1N) on a wire of

1 newton1 meter (1m) length with a current running through it perpendicularly to the magnetic lines of a field of 1 ampere (1A) has a strength of 1 tesla (1T).

Tesla is a unit of measurement of the strength of a magnetic field.

The strength of a magnetic field is denoted by a symbol B. The Lorentz force is, therefore, expressed as

F = I·L·B

where

I is the amperage of an electric current running through a wire,

L is the length of a wire,

B is the strength of an external magnetic field



All the above considerations are valid for a case of an electric current
running perpendicularly to lines of a uniform magnetic field.



As mentioned above, the Lorentz force exerted on a wire depends on the movement of electrons in the wire crossing the magnetic lines of an external magnetic field.

Simple geometry prompts us to conclude that, if the direction of the
current is not perpendicular to magnetic lines of an external magnetic
field, but at angle φ with them, the number of magnetic
lines crossed by electrons in a unit of time is smaller and, actually,
is smaller by a factor sin(φ).



So, for any angle φ between the electric current and magnetic field lines of an external magnetic field the formula for Lorentz force would be

F = I·L·B·sin(φ)

where

I is the amperage of an electric current running through a wire,

L is the length of a wire,

B is the strength of an external magnetic field

φ is the angle between the direction of the electric current and lines of an external magnetic field



Taking into consideration the direction of the Lorentz force
perpendicular to both vectors - electric current (from plus to minus)
and lines of an external uniform magnetic field (from South to North),
the above formula can be represented using a vector product

F = I ·L⨯ B  

Unizor - Physics4Teens - Electromagnetism - Magnetic Field - Inside Magnet

 



Notes to a video lecture on http://www.unizor.com



Magnetism - Internal Structure

of Magnets



Let's look inside a permanent bar magnet with two poles, North and South.

We model its magnetic properties as a result of a cumulative properties
of individual electrons rotating along parallel axes within parallel
planes in the same direction.

Each such rotating electron represent a tiny magnetic dipole with
its own North and South poles with attracting force between opposite
poles (North and South) and repelling force between the same poles
(North to North or South to South).



The attraction between two rotating electrons that face each other by
opposite poles we have explained by the fact that in this case electrons
rotate in the same direction and "help" each other. The repelling of
two rotating electrons that face each other by the same poles is
explained by the fact that they rotate in opposite directions and
"disturb" each other.



Since we are talking about permanent magnet, all axes of rotation of
electrons are always parallel to each other and planes of rotation are
always parallel as well.



Consider a situation of two electrons rotating on parallel planes around the same axis on the same radius.



In this case the magnetic properties of the South pole of the upper (on
this picture) electron are neutralized by properties of the North pole
of an electron under it.

So, the magnetic field of a pair of electrons in this position is the
same as for one electron with poles located on a greater distance from
each other.



Now expand this logic to a full size of a bar magnet. The result is that
all internal connections between South and North poles will neutralize
each other and the only significant magnetic properties are of those
electrons concentrated on two opposite surfaces of a magnet where its
North and South poles are located.



This looks like some magnetic charges of opposite types, that we called North and South, are concentrated on two opposite ends of a magnet.

These magnetic charges behave similarly to electric charges,
except magnetic ones always come in pairs. We can even think about
magnetic equivalent of the Coulomb Law. The only complication is that we
always have a superposition of two magnetic fields coming from two ends
of magnetic dipole.

This is the Gilbert model of magnetic properties, attributed to
William Gilbert, an English physician (including a physician for English
royalty), who published in 1600 a six volume treatise that contained
all the information about electricity and magnetism known at that time.
Gilbert was the one who discovered magnetic properties of Earth and came
up with formulation of properties of magnets and terminology that
describes them (like magnetic poles).



Consider a different approach - two electrons rotated within the same
plane around parallel axes and immediately near each other. The common
plane of rotation is, of course, perpendicular to the magnet's
North-South axis and axes of rotation of these electrons are parallel to
the magnet's North-South axis.



Electrons moving near each other are moving in opposite directions and
neutralize each other, as if there is no current there at all. So,
within every plane perpendicular to the North-South axis of a magnet all
inner currents are neutralized, and the only really present current is
around the outer boundary of a magnet.



This is the Ampere model of magnetism. It makes the magnetic
properties of permanent magnet equivalent to properties of an electric
current in a loop around the side surface of a magnet with each electron
moving within a plane perpendicular to a magnet's North-South axis.


This model of magnetism is extremely important, as it connects the
magnetic properties to those of properties of electric current and shows
inherent connection between electricity and magnetism.



It also opens the door to electromagnetism - generating magnetic field using electricity.

A loop of electric current acts similar to each electron inside a
permanent magnet, just on a larger scale. A number of electric current
loops of the same radius around the same axis parallel to each other
makes the magnetic field even stronger.





If we make a loop of electric current and put an iron cylinder (which by
itself does not have magnetic properties) inside this loop, the iron
cylinder will become magnetic, and the more loops the electric current
makes around this cylinder - the stronger the magnetic properties of an
iron cylinder will be, and it will act exactly as the permanent magnet,
becoming electromagnet.

But, as soon as we stop the flow of electric current around this cylinder, it will lose its magnetic properties.



Another important feature of the Ampere model is that it allows
to measure the strength of the magnetic field produced by an
electromagnet by such known physical quantities as amperage of the current circulating in the wire loops, producing the magnetic field, and some geometric properties of the wire loops.

Unizor - Physics4Teens - Electromagnetism - Magnetic Field

Notes to a video lecture on http://www.unizor.com



Magnetism - Magnetic Field



Magnetic forces act on a distance, so there must be a field that exists around each magnet - magnetic field.



When studying Electrostatics, we started with the simplest
electrically charged object - a point-object with certain excess or
deficiency of electrons to make it negatively or positively electrically
charged.

The electrostatic field around it was spherical in shape and the only
important parameter that determined the relative position of a probe
object (also a point-object, positively charged with one coulomb of
electricity) was a distance of this probe object from the source of
electrostatic field.



If we wanted to analyze the electric properties of a more complex source
of electricity, like a rod or a sphere, we could always resort to some
relatively simple geometry and calculus to achieve our goal by breaking a
larger object into smaller parts.



Looking at the electrostatic field, the forces acting on a probe object
are always unidirectional, either attracting or repelling. To calculate
the resultant force, we used a vector sum of them, and in simple cases
of sources of electrostatic fields (a point-object, a rod, a sphere) it
was relatively simple task.



With magnets the situation is much more complex. We cannot have a
point-object because each magnet has two poles and each of them act in
some way. Even more, the magnetic force exhorted by a magnet is changing
as we move from North pole to South, first diminishing to zero in the
middle and rising again at the other pole.



Probably, the simplest magnet we can deal with, as a source of magnetic
field and a probe object, is a thin rod with poles at its ends. But even
in this case we have to take into account all the different forces,
attracting and repelling, of different magnitude and directions that act
on probe magnet.



Let's experimentally visualize the magnetic field in this simplest case.

For this experiment we need a bar magnet and iron shavings. Each shaving
is a little temporary magnet that forms its poles based on the forces
of the magnetic field. Then different shavings will attach to each other
by opposite poles and form lines. The picture obtained will represent
the vectors of forces in the magnetic field of a bar magnet. Along each
line on a picture below lie iron shavings, each with North and South
magnetic poles, linked by opposite poles and directed with their South
pole closer to North pole of a bar magnet.



The picture below schematically represents these field forces.



Direction of forces from North magnetic pole to South was traditionally
chosen, similarly to a direction of the electric current was chosen from
a positive terminal to a negative one, regardless of the flow of
electrons, unknown at the time of early experiments with electricity.



Let's discuss a concept of a magnetic field.

As usually, the following explanation is the model, which to some
degree corresponds to experimental and theoretical data, but we do not
claim that in reality the things are arranged in exactly this way.

However, we offer it as an aid to understanding the concept of a magnetic field.



Imagine a small particle rotating within a plane with certain speed on a
certain radius around an axis that is perpendicular to this plane. On
the same axis in a plane parallel to the first one another particle is
rotating. Generally speaking, it might rotate on a different radius, in
the same or opposite direction and with a different speed.



Consider a distance between these two parallel planes of rotation of
these two particles. When it's large, particles don't really have any
interaction. But, when we make this distance small enough, the particles
will "feel" each other.



If the particles rotate in the same direction, there will be some
attracting force between them and the planes of rotation tend to get
closer to each other.

If the particles rotate in the opposite directions, there will be some
repelling force between them and the planes of rotation tend to increase
the distance between them.



The rotating particles in this model behaves like a bar magnets
positioned along the axis of rotation with poles determined by a
direction of rotation. We can assume that the North pole is defined by a
rule, that, looking from it towards the rotating particle, this
particle rotates counterclockwise.

If two particles rotate around the same axis in the same direction, each
behaving like a bar magnet, the magnets will attract to each other
because they will be facing by opposite poles.

If the particles rotate in opposite direction, the corresponding magnets
will be facing each other by the same pole and will repel each other.



Now let's assume that these particles are electrons rotating around a
nucleus in the atoms inside some object. According to this model, if all
planes of rotation of electrons inside all atoms are parallel and the
rotation is such that all North poles of all atoms are directed in the
same way, we have a perfect permanent magnet.



If planes of electron rotation in some object are randomly directed and
are insensitive to outside forces exhorted by magnets, we have a
diamagnetic object - the one that cannot be magnetized.



If planes of electron rotation in some object are randomly directed, but
outside magnetic forces, interacting with atoms of this object, align
all planes of rotation in a parallel fashion with the same direction of
the poles, we have an object that can be a temporary magnet.



In all those cases our model of rotating electrons, producing a force
that in some way acts like a bar magnet positioned along the axis of
rotation, seems to explain all the magnetic properties.

It also prompts to a connection between the electricity and magnetism
because both are caused by position and movement of electrons.

Unizor - Physics4Teens - Magnets - Practical Aspects

Notes to a video lecture on http://www.unizor.com



Magnetism - Practical Aspects



Here is a list of a few cases where permanent magnets of different kind are used.



A magnetic screwdriver.

Refrigerator door.

Magnetic letters.

Bracelets with magnetic closure.

Compass.

Magnetic toys.

Different machinery uses magnets (e.g. large disk magnets to pick up metal junk).

Medical instruments (e.g. MRI - Magnetic Resonance Imaging).

In phones and headphones.

In all kinds of motors and generators.

In televisions.

In computers.



Permanent magnets occur in nature. A mineral magnetite is such a permanent magnet. It's black and shiny, when polished. The chemical composition of magnetite is iron oxide, which means that its molecule contains only atoms of iron and oxygen, the formula is Fe₃O₄.

Two pieces of magnetite will attract each other if faced by
opposite poles (North of one to South of another) and repel each other
when positioned facing each other by the same pole.



Magnetite attracts certain metals, like iron.



A piece of magnetite, if hanging on a thread or free floating in
water on a wooden plate will always turn along a meridian, thus people
used it in navigation before they invented a compass.



The naturally occurring magnetite is quite a weak magnet. Much
stronger permanent magnets are created artificially by melting together
certain metals. One of the strongest artificial magnets are made by
combining iron, neodymium and boron into an alloy called neodymium magnets.



Artificial magnets can have any shape with location of the poles chosen
by a manufacturer. For example, a ring magnet can be created with a
North pole on the outside circumference of a ring and South pole on the
inside circumference.



Consider a bar magnet with poles on its opposite sides.

Let's use an iron nail as a probe object to measure the force of attraction at different points on a magnet.

The strongest force of attraction will be at the ends of a bar magnet,
at its poles. If we move a nail from one end of the magnet to another,
the strength of attraction will diminish to zero at the middle, then
again will rise to its maximum on an opposite pole.

The midpoint of a bar magnet has no attracting strength at all.



Interestingly, if we break a bar magnet in the middle, each half will
not be a single pole magnet, single pole magnets don't exist. Each half
will have two poles, one old and the new one at the point we broke the
original magnet. Each new smaller magnet will be weaker than original.





Artificial magnets can be permanent or temporary.
Permanent magnets do not change their magnetic properties. Temporary
ones can be magnetized, when are near another permanent magnet, or
demagnetized, when there is no other magnets nearby. Plain nails and
paperclips have such a property. Their polarity depends on the position
of the other permanent magnet. Another example is electromagnets that
will be discussed later on in the contents of a connection between
electricity and magnetism.



There are artificial magnets that, after being magnetized by electric
impulse, retain their magnetic properties, including the polarity. At
the same time, exposed to another impulse, they can lose their magnetic
properties or change the polarity. This type of magnets were used in the
memory of the first computers with each bit of information (1 or 0)
stored as a magnetization of one ferrite ring.





Artificial magnets can be not only in some solid shape, but also form a
thin magnetic layer on a surface of some other material. This is how
magnetic tape and magnetic disks were created, both used extensively in
the computers. The principle of work of these memory devices is based on
the properties of the thin magnetic layer to retain the state of tiny
magnets this layer contains. Special devices can "write" information on
the magnetic layer by temporary magnetizing the tiny magnets of the
layer and "read" this information.



Another example is injecting a magnetically-sensitive liquid into a
tumor and, using a powerful magnet, heat it up to destroy the tumor.



The fact that permanent magnets are permanent and, seemingly, represent
an unlimited source of energy, prompted many people to construct a
device that would exploit this property to create a perpetual movement
and use it to generate unlimited amount of power.



Some of these devices did move for a long time. However, they contradict
the principle of energy conservation for a closed system and, sooner or
later, friction and other forces would stop it.

Here is a good example of such a device



https://www.youtube.com/watch?v=UqlPePYgdg4