Friday, April 27, 2018
Unizor - Physics - Mechanics - Kinematics - Galileo's Relativity Principle
Notes to a video lecture on http://www.unizor.com
Galileo's Relativity Principle
Galileo's Relativity Principle is experimentally obtained result that states that
the same mechanical experiment conducted in two different inertial frames produces the same results.
We accept this as an axiom, which has very deep meanings. Some of them are specified implicitly by omission, some are explicitly stated.
Galileo's Relativity Principle implies the possibility of space and time
separation between two equivalently organized experiments, since it
does not require any location coincidence or simultaneousness of
conducting these experiments.
Let's start with a concept of time.
By omitting any time requirements, the Principle implies that the flow of time does not change the results of experiment. Today's 10 seconds of time are equivalent to yesterday's or tomorrow's 10 second.
Time is completely symmetrical towards past or future at any moment.
In other words, time is invariant relative to any moment (or uniform, or isomorphic).
Now let's analyze the space. Here, again, the Relativity Principle does not specify any dependency of the results of an experiment from the location. So, space is invariant relative to location, in other words, space is uniform (or isomorphic).
Similarly, the results of experiment are independent of orientation of
an apparatus used to conduct this experiment in space. Any direction is
no different than any other. So, the Relativity Principle implies that space is invariant relative to any direction, that is space is isotropic.
All the above implications are quite fundamental and intuitively
obvious, but the most interesting meaning of the Relativity Principle is
explicitly specified. It states that there is no experiment that would
allow to differentiate one inertial system from another. In other words,
the motion of an inertial system cannot be detected from inside.
Consider two people in different inertial systems. For example, one is
on the ground and another is on a train without windows going along a
straight line with the same speed. Let's ignore the curvature of the
Earth and its gravitation directed perpendicularly down and balanced by
the reaction of the ground for a person on the ground and the reaction
of the train's floor for a person on a train. The Relativity Principle
states that there is no experiment that the person on a train can
conduct that would tell him that he is moving relative to the ground,
his results would be identical to those that a person on the ground has.
For instance, if both of them take balls of the same weight and size and
roll it with the same effort, the balls will roll with the same speed,
one - relative to the ground, another - relative to the train's floor.
The water in the pot standing still on the floor of the train will look
exactly like a similar pot with water on the ground - no waves, the
level is strictly horizontal.
The weight of an object on the ground will be the same as on the train.
A bullet on the train will cover the same distance in certain amount of
time relative to the train as in case of a bullet shut by a person on
the ground.
We can come up with many experiments, and all of them will show identical results.
Here we have to bring attention to the words "relative to" used in all
the above cases. They signify the connection of results of any
experiment to the frame of reference. All these results are
"relative". Speed of the rolling ball in the above example is the same,
if we measure it separately in two different inertial frames -
one connected to the ground, another - to the train. Similarly, the
speed and distance covered in certain time by a bullet were measured
separately with identical results.
While such important characteristics like distance and speed are obviously relative to a frame of reference, one physical characteristic is considered absolute in classical Physics. It's time.
We always assume that the clocks in the hands of a person on the ground
are identical to clocks on the train. If two people synchronized their
ideal clocks, one boarded our train, while another remains on the
ground, their clocks will remain synchronized, no matter how far and how
long the train goes.
So, time is absolute in classical Physics, while such physical characteristics as distance and speed are relative to the frame of reference. This Galileo's Relativity Principle predates Einstein's Theory of Relativity that developed this principle much further.
Thursday, April 26, 2018
Unizor - Physics - Mechanics - Kinematics - Non Inertial Reference Frames
Notes to a video lecture on http://www.unizor.com
Non-Inertial Frame of Reference
Definition of non-inertial frame of reference is simple. Any frame of reference that is not inertial is non-inertial.
Recalling the definition of inertial frames as those where the Law of Inertia holds true, we can say that non-inertial frame is a frame where the Law of Inertia does not hold true.
To get a feel of non-inertial frames, let's consider a few examples.
Example 1
Let's start with inertial frame of reference XYZ and an object at point P(1,0,0) at rest. There are no forces acting on it, so it stays at rest at the same point P(1,0,0).
Now consider a system of coordinates UVW with an origin coinciding with
an origin of XYZ frame, the W-axis coinciding with Z-axis of XYZ frame
and uniformly rotating (relative to XYZ frame) counterclockwise around
the W-axis with angular speed ω.
It is easily seen that point P in UVW system of
coordinates rotates clockwise around the origin of coordinates within
UV-plane along a circle of radius 1 with an angular speed ω.
So, we have a situation when there are no forces acting upon our object,
yet it rotates in UVW frame along a circular trajectory - definite
disagreement with the Law of Inertia that states that an object,
not acted upon by unbalanced forces, should stay at rest or move with a
constant vector of velocity, which implies that its trajectory must be a
straight line.
Therefore, this UVW frame is not inertial, hence non-inertial.
Example 2
Let's start with inertial frame of reference XYZ and an object at point P(1,0,0) at rest. There are no forces acting on it, so it stays at rest at the same point P(1,0,0).
Now consider a system of coordinates UVW with the origin initially (at t=0)
coinciding with the origin of XYZ frame and all axes initially
coinciding with corresponding axes of XYZ frame. Now assume that UVW
system started to move along the U-axis forward with constant
acceleration a.
It is easily seen that point P in UVW system of coordinates moves along the U-axis in negative direction with constant acceleration a.
So, we have a situation when there are no forces acting upon our object, yet it moves with constant acceleration −a in UVW frame along the U-axis, thus changing its velocity in magnitude - definite disagreement with the Law of Inertia that states that in this case in the inertial frame an object should move with constant velocity (direction and magnitude).
Therefore, this UVW frame is not inertial, hence non-inertial.
Generally speaking, if the origin of UVW frame is not uniformly moving relative to the origin of inertial frame XYZ, while axes of these frames are correspondingly parallel, the frame UVW is non-inertial.
The proof is simple.
If in one frame the position of an object at any moment in time is Pxyz(t) and in another frame the position of the same object is Puvw(t) and the position of the origin of UVW frame in XYZ-coordinates is Qxyz(t) these positions are related as
Pxyz(t) = Puvw(t) + Qxyz(t)
Since XYZ is inertial frame, an object that is not acted upon by
any unbalance force moves along a straight line with constant velocity
vector (that might be a zero vector). That means, the function Pxyz(t) is linear function of time t for each of its component x, y and z.
If the origin of UVW frame is not uniformly moving relative to the origin of inertial frame XYZ, function Qxyz(t) is not linear for its components (otherwise, it would move uniformly).
Therefore, function Puvw(t) cannot be linear, which means an object moves in the UVW in a non-uniform mode.
So, we see that an object, free from all actions by unbalanced forces,
does not move uniformly in UVW frame. Hence, the frame is non-inertial.
Wednesday, April 25, 2018
Unizor - Physics - Mechanics - Inertial Frame of Reference
Notes to a video lecture on http://www.unizor.com
Inertial Frame of Reference
The term frame of reference in the context of Mechanics is understood in the same sense as the system of coordinates.
Since coordinates depend on the system of coordinates, the position functions we were dealing with (x(t), y(t) and z(t)) are obviously related to a system of coordinates established in our three-dimensional space.
Assume, for example, that in one system of XYZ-coordinates (or frame of reference, or just frame) our position functions are
x(t) = t²
y(t) = 0
z(t) = 0
Consider a new frame with UVW-coordinates originated at point (3,0,−5)
in the old frame with axes correspondingly parallel to those of the old
frame.
In this new frame the coordinates will be different:
u(t) = t²−3
v(t) = 0
w(t) = 5
So, when we talk about position functions or their derivatives (velocities, accelerations), we always have in mind some frame of reference or system of coordinates, relative to which the position is defined.
In philosophical sense the position of any object is absolute, but, if
we want to express this position in some numerical way, it's always
relative to some chosen frame of reference.
If the frame of reference is not defined (at least, implicitly, like,
when we say that the speed of a car is 60 km/hour, we mean "relative to
the road", which defines a frame of reference), we cannot quantitatively
talk about position and other quantitative characteristics like
velocity or acceleration.
Obviously, we would like to have an absolute frame of reference, which is absolutely
not moving anywhere and can be used as The Main Frame of Reference,
relative to which all other objects and frames can be referenced.
Alas, there is no such absolute reference frame because everything in this Universe is moving somewhere somehow relative to something.
However, the next best thing would be a reference frame tied to position
of stars, because they are so far away that seem standing still. This
reference frame we will keep in mind in those rare cases when we mention
motion without explicitly or implicitly referring to any particular
frame.
Imagine a comet in space flying far from any solar system, so there are
almost no gravitation fields around, no any other forces that can change
this comet's course. Relative to stars that are almost standing still,
this comet moves almost in the same direction with almost constant
velocity. This is an almost uniform motion relatively to almost steady
reference frame and the best approximation to an abstract concept of uniform motion in an inertial reference frame.
We have just introduced a new term inertial reference frame that we explain below.
The almost uniform motion of a comet far from any forces of gravity is the basis for the Law of Inertia that should be considered as an axiom confirmed by experiments. It states that an object at rest stays at rest and an object in uniform motion stays in this uniform motion (that is, no change in velocity vector), unless acted upon by unbalanced forces.
Inertia is the property of an object to stay at rest or maintain its uniform motion in the absence of unbalanced forces.
That's why the Law above is called the Law of Inertia, and that's why
the frame of reference related to almost immovable stars where this
phenomenon takes place is called inertial frame of reference.
The most difficult part in understanding of this Law of Inertia is to understand the meaning of the state of rest or uniform motion
since no system of coordinates is mentioned. Indeed, if in one
reference frame an object moves uniformly with some velocity vector, in
another system, moving relatively to the first, the velocity vector,
represented as derivatives of its coordinates, looks differently and not
necessarily be a constant, as required in uniform motion.
We can overcome this difficulty and say that the one and only reference frame implied in the Law of Inertia
is the one based on almost immovable star-based frame. That's good
enough as the first step, but we will always want to use different
systems in solving different mechanical problems and in most cases it's
inconvenient to use this system. For example, if a car moves along a
straight road, we would like a reference frame originated at the car's
starting point on Earth and X-axis going along the road, assuming it's a
straight line and not too long, so we can ignore the curvature of our
planet.
But here is an interesting consideration. Assume, an object is in
uniform motion relative to some XYZ frame of reference (say, our
star-based one) and another UVW frame of reference is in uniform motion
relatively to the first one with corresponding axes parallel to each
other.
The uniform motion of an object in the XYZ frame, as we know, can be expressed as
x(t) = a·t + x0
y(t) = b·t + y0
z(t) = c·t + z0
Or in vector form
P(t) = t·V + P0
where the velocity vector
V = {a, b, c}
and initial position
P0 = {x0, y0, z0}
When the UVW frame uniformly moves relative to XYZ frame with correspondingly parallel axes according to some velocity vector Ω , coordinates of the same object in different frames of reference are related as linear functions of time.
If in one frame the position of object at any moment in time is Pxyz(t) and in another frame the position of the same object is Puvw(t), these positions are related as
Pxyz(t) = Puvw(t) + t·Ω + Q0
where Ω is a velocity vector of the origin of the UVW frame relative to XYZ frame and Q0 is the initial position of the origin of the UVW frame relative to XYZ frame at time t=0.
Here is the logic behind this equation.
At time t=0 an object is at position
At the same time it is at position Puvw(0) in UVW frame, which is shifted by vector Q0 in XYZ frame from its origin.
Since a vector Pxyz(0) from the origin of XYZ frame to an object's position at time t=0 equals to a sum of a vector from the origin of XYZ frame to the origin of UVW frame Q0 and a vector from the origin of UVW frame to an object Puvw(0), our equation is true for the initial time moment t=0.
As the time goes, the origin of the UVW frame moves to
Pxyz(t) = Puvw(t) + t·Ω + Q0
Differentiating both sides, we will get an equation about velocities of our object in two frames of reference:
Vxyz(t) = Vuvw(t) + Ω
This equation shows that if the vector of object's velocity is constant in one frame, it's constant in another since vector Ω , characterizing the uniform movement of frame UVW relative to frame XYZ, is constant.
Consider now any frame of reference moving uniformly relative to a star-based frame. Since the Law of Inertia
is an axiom in the star-based frame, we can now say that the object,
moving uniformly in this system, moves uniformly in any other system
that uniformly moves relative to a star-based.
That's why any frame of reference moving uniformly relative to a star-based frame, is also an inertial frame, since the Law of Inertia is true in it.
So, we have postulated that the Law of Inertia is true for star-based frame. Based on that, we called this coordinate system an inertial frame of reference. Then we have proved that in any other frame of reference, moving uniformly relative to a star-based one, the Law of Inertia is true as well, which allowed to call that other frame also an inertial frame of reference.
As well as our chosen system of coordinates moves approximately uniformly relative to a star-based one, it can be called an inertial frame of reference and the Law of Inertia is expected to be true in it (within certain precision, of course).
Monday, April 23, 2018
Unizor - Physics - Mechanics - Kinematics - Rotation
Notes to a video lecture on http://www.unizor.com
Rotation
Let's consider a rotation of an object within XY-plane around Z-axis along a circular trajectory of radius R with a center at the origin of coordinate.
Obviously, its Z-coordinate will always be zero, that is z(t)=0, but X- and Y-coordinates will somehow depend on time t.
We would like this motion to be uniform in some sense, but we have to define what we really mean calling this motion a uniform rotation.
Recall that the term uniform motion we used in a sense that an
object moves along a straight line with constant velocity, covering the
same distance in the same intervals of time.
When dealing with rotation, the concept of distance along a straight line should be replaced with a concept of angle of rotation. Inasmuch as we cover the same linear distance in uniform motion during the same intervals of time, in case of uniform rotation we cover the same angle of rotation during the same intervals of time.
Assume that in the beginning of rotation our object is at point
Since during the rotation along a circular trajectory the distance between an object and the origin of coordinates is constant R, we can express coordinate functions as functions of an angle of rotation, like in polar coordinates:
x(t) = R·cos(φ(t))
y(t) = R·sin(φ(t))
Since we are analyzing the uniform rotation, and this uniformity
means that we rotate by the same angle during the same intervals of
time, we define this motion as a rotation with constant angular speed φ'(t) - constant first derivative of an angle of rotation by time.
Assume, angular speed φ'(t)=ω (constant).
Then angle of rotation
is an angle from the positive direction of the X-axis to a vector from
the origin of coordinates to a position of our object at the beginning
of motion at t=0. Since we assumed that the object starts from a point
Now we can easily find the coordinate functions of the position of an object:
x(t) = R·cos(ω·t)
y(t) = R·sin(ω·t)
z(t) = 0
Taking the first derivative from these functions, we find the components of the velocity vector:
x'(t) = −R·ω·sin(ω·t)
y'(t) = R·ω·cos(ω·t)
z'(t) = 0
Out of curiosity, let's calculate the scalar product of the position vector
It's equal to
[R·cos(ω·t)]·[−R·ω·sin(ω·t)] +
+ [R·sin(ω·t)]·[R·ω·cos(ω·t)] =
= 0
As we know, if the scalar product of two vectors is zero, they are perpendicular to each other. Therefore, a velocity vector in uniform rotation is perpendicular to a position vector.
Since the latter is a radius from a center of a trajectory circle to a
point where the object is located, the perpendicular to this radius -
the velocity vector - is a tangential line to this circle at this point.
So, we have found an interesting property of a velocity vector during a uniform rotation - it's always tangential to a trajectory at a point of position of a rotating object.
Taking derivative from velocity functions, we find the components of the acceleration vector:
x'(t) = −R·ω²·cos(ω·t)
y'(t) = −R·ω²·sin(ω·t)
z'(t) = 0
Notice that this vector is equal to a position vector multiplied by −ω². It means that its direction is exactly opposite to a position vector, that is directed towards the center of rotation.
So, we have found an interesting property of an acceleration vector during a uniform rotation - it's always directed towards a center of rotation.
Unizor - Physics - Mechanics - Kinematics - Constant Acceleration
Notes to a video lecture on http://www.unizor.com
Constant Acceleration
Let's consider a motion with constant vector of acceleration from the position of Kinematics and derive simple equations that mathematically describe this motion in coordinate system.
Since acceleration is the second derivative of a position function and also the first derivative of a velocity, the motion with constant vector of acceleration
x"(t) = a
y"(t) = b
z"(t) = c
where a, b and c are constants
and at least one of these constants is not zero (otherwise, we deal
with a case of uniform motion considered in the previous lecture).
Let's represent this in vector form, considering that components of the position vector P(t) are coordinate functions x(t), y(t) and z(t):
P(t) = {x(t), y(t), z(t)}
P'(t) = {x'(t), y'(t), z'(t)}
P"(t) = {x"(t), y"(t), z"(t)}
Therefore, in vector form equation of motion with constant acceleration vector A is:
P"(t) = A
The only function, whose derivative is constant, is a linear function. Hence, the first derivative of position of our object, that is its velocity vector, can be described by linear functions of time:
x'(t) = a·t + vx(0)
y'(t) = b·t + vy(0)
z'(t) = c·t + vz(0)
where vx(0), vy(0) and vz(0) are some constants.
We have chosen the names of these constants to emphasize their meaning - components of velocity vector V(t) at time t=0:
x'(0) = vx(0)
y'(0) = vy(0)
z'(0) = vz(0)
or, in vector form,
V(0) = {vx(0), vy(0). vz(0)}
Continuing the vector representation of our equations of motion, we can express velocity vector V(t) as a linear function of time using acceleration vector A and initial velocity vector V(0) as parameters:
V(t) = A·t + V(0)
Now, since we have the first derivatives of position functions, let's get the position functions themselves.
The only function, whose derivative is a linear function, is a quadratic function. Hence, the position functions can be described by quadratic functions of time:
x(t) = a·t²/2 + vx(0)·t + x0
y(t) = b·t²/2 + vy(0)·t + y0
z(t) = c·t²/2 + vz(0)·t + z0
where x0, y0 and z0 are some constants equal to position of our object at time t=0:
x(0) = x0
y(0) = y0
z(0) = z0
In vector form the above equations of motion can be represented shorter:
P(t) = A·t²/2 + V0·t + P0,
where V0 = V(0) - initial velocity vector and P0 = P(0) - initial position.
Obviously, the second derivatives of these three quadratic functions above correspondingly equal to a, b and c - components of our constant acceleration vector of motion.
How to determine constants vx(0), vy(0), vz(0), x0, y0 and z0 that participate in the equations for position of our object?
Well, we cannot without additional information.
As we have determined,
By itself, constant acceleration vector does not define the motion, we need an initial position and initial velocity as well.
Knowing all of these, an initial position, an initial velocity vector and a constant vector of acceleration, we can find equations of motion for x(t), y(t) and z(t).
Does a motion with constant acceleration occurs along a straight line?
The answer depends on collinearity between an acceleration vector and a vector of initial velocity. The trajectory is a straight line if these two vectors are collinear, that is
k·a = vx(0)
k·b = vy(0)
k·c = vz(0)
Or in vector form
k·A = V0
In such a case
x(t) = a·(t²/2 + k·t) + x0
y(t) = b·(t²/2 + k·t) + y0
z(t) = c·(t²/2 + k·t) + z0
Or in vector form
P(t) = A·(t²/2 + k·t) + P0
The equations above define a trajectory collinear to vector
If the motion with a constant acceleration occurs within a
straight line (like in case of a car, accelerating along a straight
road), it's very convenient to choose a system of coordinates, where
X-axis coincides with this line and the positive direction of the X-axis
coincides with the direction of the motion.
Then y(t)=z(t)=0 and y'(t)=z'(t)=0 for all moments of time t. In particular, velocity vector looks now as
For these cases traditionally the letter v is used for the X-component of the velocity vector. So, we will use in these cases the symbol v(t) for X-component of the velocity vector x'(t).
The only non-trivial equation of motion then will be about x(t):
x(t) = a·t²/2 + v0·t + x0
(where x0=x(0) is initial position, v0=v(0) is initial speed of an object at the start of motion and a - its constant acceleration).
If the origin of the system of coordinates coincides with the initial position of the object, x0=0 and the equation of motion looks simpler:
x(t) = a·t²/2 + v0·t
If, in addition, the object is at rest in the beginning of motion, v0=0 and the equation of motion looks really simple:
x(t) = a·t²/2
Since the positive direction of the X-axis is the same as the direction of the movement, velocity vector's direction plays minimal role, and only its magnitude (positive) is important, in which case we can use the term speed for v(t) instead of velocity.
CONCLUSION
An object moving from the initial position
x(t) = a·t²/2 + vx(0)·t + x0
y(t) = b·t²/2 + vy(0)·t + y0
z(t) = c·t²/2 + vz(0)·t + z0
Or, in vector form,
P(t) = A·t²/2 + V0·t + P0
If the initial position of an object is on the X-axis, initial velocity vector and acceleration vector are colinear with the X-axis, the equations are simplified:
x(t) = a·t²/2 + v0·t + x0
y(t) = 0
z(t) = 0
If, in addition, the origin of coordinates coincides with the point of beginning of motion, that is x0=0, the equations are simplified even further:
x(t) = a·t²/2 + v0·t
y(t) = 0
z(t) = 0
Finally, if, in addition, the starting velocity is zero, that is v0=0, the equations are simplified even further:
x(t) = a·t²/2
y(t) = 0
z(t) = 0
Unizor - Physics - Mechanics - Kinematics - Uniform Motion
Notes to a video lecture on http://www.unizor.com
Uniform Motion
Let's consider a uniform motion from the position of Kinematics and
derive simple equations that mathematically describe this motion in
coordinate system.
The uniform motion along a straight line is characterized by two factors: its trajectory is a straight line in space and its velocity vector is constant, that is each component of the velocity vector does not change with time to assure the direction and magnitude of velocity are constant.
Actually, the second condition (velocity vector is constant) is sufficient for the first, which we will prove.
So, assume that velocity vector V is constant with coordinates
It means that, if x(t), y(t) and z(t) are coordinate functions defining the position vector P of our object, the derivatives of these functions are constant:
x'(t) = a
y'(t) = b
z'(t) = c
where a, b and c are constants
and at least one of these constants is not zero (otherwise, we deal
with a trivial case of object at rest considered in one of the earlier
lectures).
These three equations of motion for each coordinate can be written in vector form as
P' = V,
where derivative of a vector P' means a vector of derivatives
The only function, whose derivative is constant, is a linear function.
Hence, the position of our object can be described by linear functions
of time:
x(t) = a·t + x0
y(t) = b·t + y0
z(t) = c·t + z0
where x0, y0 and z0 are some constants.
Obviously, the derivatives of these three functions representing the position correspondingly equal to a, b and c - components of our constant velocity vector of motion.
How to determine constants x0, y0 and z0 that participate in the equations for position of our object?
Well, we cannot without additional information.
Notice that for t=0 (that is, at the beginning of motion)
x(0) = a·0 + x0 = x0,
y(0) = b·0 + y0 = y0,
z(0) = c·0 + z0 = z0.
Therefore, we can say that
Let vector P0 represent the initial position
P(t) = t·V + P0
By itself, velocity does not define the motion, we need an initial position as well.
Knowing both, an initial position and a constant vector of velocity, we can find equations of motion for x(t), y(t) and z(t).
Let's now prove that the motion described by equations
x(t) = a·t + x0
y(t) = b·t + y0
z(t) = c·t + z0
goes along a straight line.
To prove this, we will prove that any two vectors from the point where the motion started
In other words, we will prove that for some real number k the following is true:
P0P1 = k·P0P2
Vector P0P1 has coordinates equal to a difference between coordinates of
P0P1 =
={x(t1)−x0, y(t1)−y0, z(t1)−z0}=
= {a·t1, b·t1, c·t1}
Vector P0P2 has coordinates equal to a difference between coordinates of
P0P2 =
={x(t2)−x0, y(t2)−y0, z(t2)−z0}=
= {a·t2, b·t2, c·t2}
Obviously, vectors
P0P1 = {a·t1, b·t1, c·t1} =
= t1·{a, b, c} = t1·V
and
P0P2 = {a·t2, b·t2, c·t2} =
= t2·{a, b, c} = t2·V
are collinear to each other:
P0P1 = (t1/t2)·P0P2
In addition, both these vectors are collinear to velocity vector
End of proof.
Since uniform motion is a motion along a straight line, it's very
convenient to choose a system of coordinates, where X-axis coincides
with this line and the positive direction of the X-axis coincides with
the direction of the motion.
Then y(t)=z(t)=0 and y'(t)=z'(t)=0 for all moments of time t. In particular, velocity vector looks now as
For these cases traditionally the letter v is used for the X-component of the velocity vector.
The only non-trivial equation of motion then will be about x(t):
x(t) = v·t + x0
If the origin of the system of coordinates coincides with the initial position of the object, x0=0 and the equation of motion looks really simple:
x(t) = v·t
Since the positive direction of the X-axis is the same as the direction of the movement, velocity vector's direction plays minimal role, and only its magnitude (positive) is important, in which case we can use the term speed for v in the above equation of motion.
CONCLUSION
An object moving from the initial position
x(t) = a·t + x0
y(t) = b·t + y0
z(t) = c·t + z0
Or in vector form
P(t) = t·V + P0
If the X-axis coincides with the line of motion and a vector of velocity has X-component v (Y- and Z-comonents are, of course, equal to zero), the equations are simplified:
x(t) = v·t + x0
y(t) = 0
z(t) = 0
If, in addition, the origin of coordinates coincides with the point of beginning of motion, that is x0=0, the equations are simplified even further:
x(t) = v·t
y(t) = 0
z(t) = 0
Friday, April 20, 2018
Unizor - Physics - Mechanics - Kinematics - Problems
Notes to a video lecture on http://www.unizor.com
Problems on Kinematics
In these and most other cases the units of distance are a meters and derived from it units (like kilometers, millimeters etc.), unit of time is a second or an hour, unless otherwise explicitly specified
Problem 1
Assume a motion along a straight line coinciding with X-axis and represented by a position functions
x(t)=t2, y(t)=0, z(t)=0.
What form the position functions will take in a new coordinate system
with the new origin at old coordinates (5,0,0) and all new axes parallel
and similarly directed to old axes?
Answer:
x(t)=t2−5, y(t)=0, z(t)=0.
Problem 2
An object is falling down along the Z-axis from a point
x(t) = 0
y(t) = 0
z(t) = 25 − t²/4
How long will it take for this object to hit the ground?
Answer:
T = 10
Problem 3
An object is falling down along the Z-axis from a point
x(t) = 0
y(t) = 0
z(t) = 25 − t²/4
What is the object's speed when it hits the ground?
Answer:
V = −5 m/sec
Problem 4
A projectile is launched from the ground within a vertical XZ-plane at
an angle to horizon. It moves according to the following coordinate
functions:
x(t) = 2·t
y(t) = 0
z(t) = 10·t−t²
How far will it fly until landing to the ground?
Answer:
20 m
Problem 5
A train goes from point A to point B. The distance between these points
is 720 km. The first half of this distance a train moves with an average
speed of 60 km/hr. The second half of the distance it moves with an
average speed of 90 km/hr.
What is the average speed of this train on its way from A to B in km/hr and m/sec?
Answer:
72 km/hr = 20 m/sec
Problem 6
A train goes from point A to point B, and the entire travel time is 10
hours. The first and the last time intervals of one hour a train
accelerates and decelerates and moves with an average speed of 60 km/hr.
The rest of the entire time (between acceleration and deceleration) it
moves with an average speed of 90 km/hr.
What is the distance from A to B? What is the average speed of a train on its way from A to B in km/hr?
Answer:
840 km; 84 km/hr
Thursday, April 19, 2018
Unizor - Physics4Teens - Mechanics - Kinematics
Notes to a video lecture on http://www.unizor.com
Graphical Representation
of Motion
We have studied three categories of functions:
position (coordinate) functions x(t), y(t) and z(t) to define the position of an object in three-dimensional space, using their Cartesian coordinates as functions of time t;
velocity functions x'(t), y'(t) and z'(t) to define the rate of change of position of an object in three-dimensional space; these functions are first derivatives of corresponding position functions;
acceleration functions x"(t), y"(t) and z"(t) to define the rate of change of velocity of an object in three-dimensional space; these functions are second derivatives of corresponding position functions.
In general, to graphically analyze any function y=f(x) of a single argument x, we use two-dimensional plane with XY-coordinates and construct a graph of this function as a set of all points
We will do this analysis for each characteristic of motion as function of time argument t (position, velocity and acceleration) in some simple cases.
Our main case is a motion along the straight line. It simplifies our
analysis, as we can choose an X-axis coinciding with the line of motion,
and Y- and Z-coordinates of an object will always be zero. So, we will
have only one set of functions - x(t), x'(t) and x"(t) to analyze.
We will also extend the time line to both directions, positive (future)
and negative (past), because our null-moment is chosen arbitrarily.
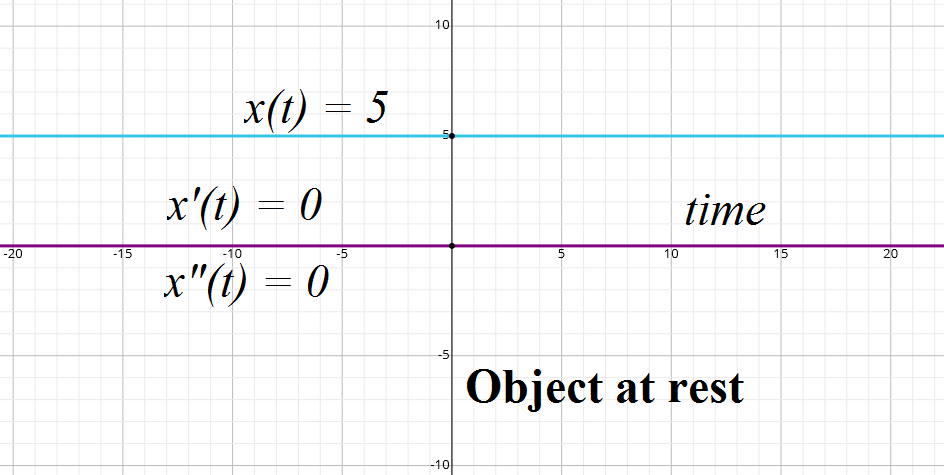
Our first case is an object at rest. Its X-coordinate is constant: x(t)=5. The first and second derivatives of this function are zero: x'(t)=0, x"(t)=0. Graphically, all three characteristics of motion look like this:
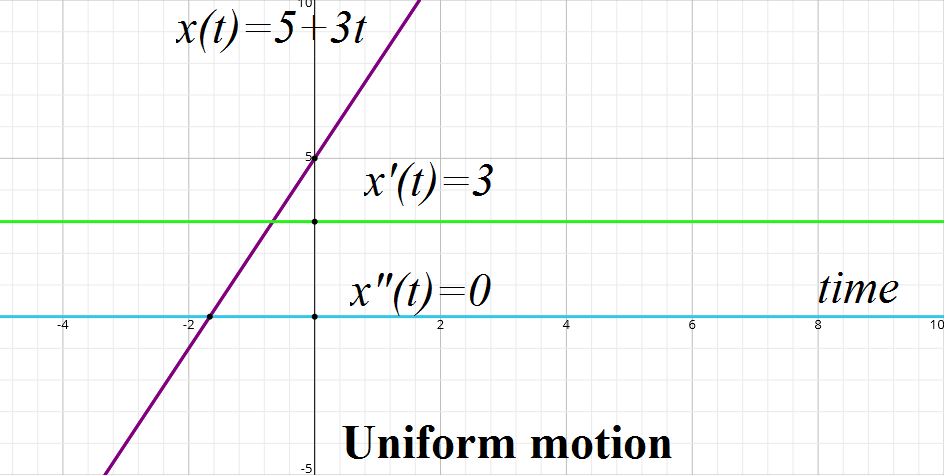
Next let's consider a uniform motion along an X-axis, according to position function x(t)=5+3t. Its velocity function (the first derivative of position) is x'(t)=3 (constant for uniform motion) and its acceleration (second derivative) is x"(t)=0. Graphically, all three characteristics of motion look like this:
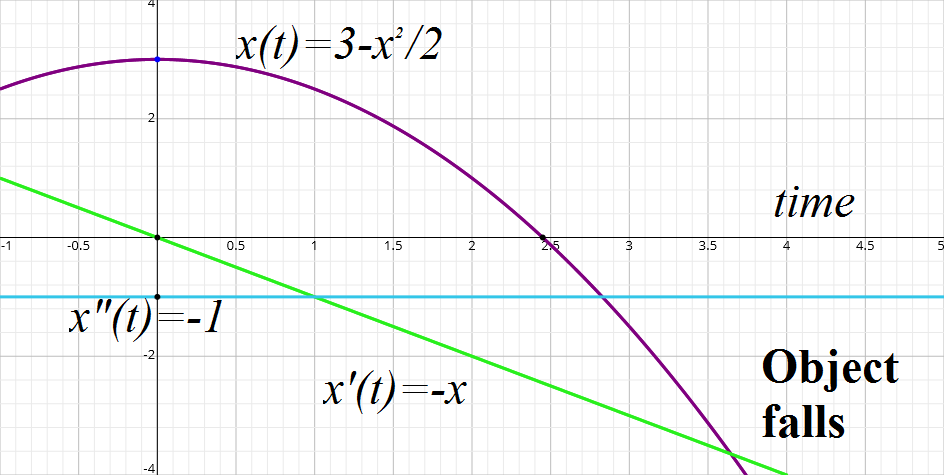
Now let's consider a case of an object falling from some height down along an X-axis, according to position function x(t)=3−t²/2. Its velocity function (the first derivative of position) is x'(t)=−t and its acceleration (second derivative) is x"(t)=−1 (constant). Graphically, all three characteristics of motion look like this:
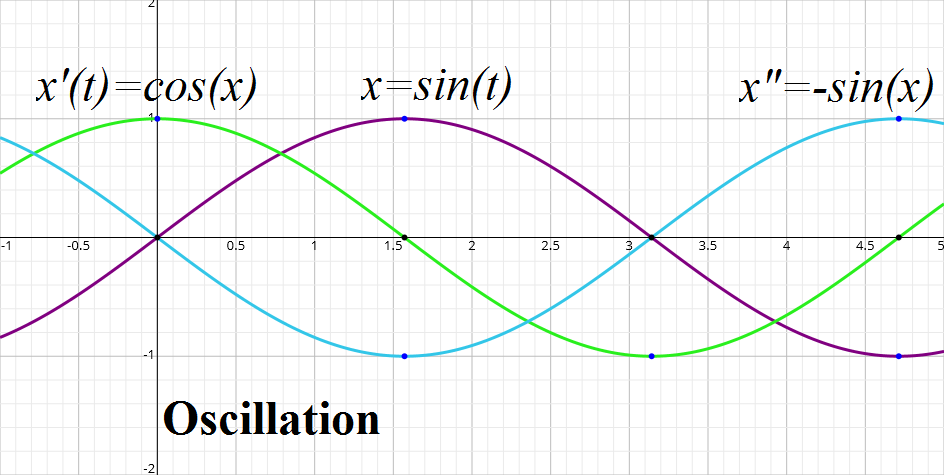
Finally, let's consider a case of an object oscillating left and right
along an X-axis around point 0, according to position function x(t)=sin(t). Its velocity function (the first derivative of position) is x'(t)=cos(t) and its acceleration (second derivative) is x"(t)=−sin(t). Graphically, all three characteristics of motion look like this:
Tuesday, April 17, 2018
Unizor - Physics4Teens - Mechanics - Kinematics - Acceleration
Notes to a video lecture on http://www.unizor.com
Acceleration
Recall that, if x(t), y(t) and z(t) are coordinate functions of the moving object, the derivatives of these functions x'(t), y'(t) and z'(t) represent components of a velocity of this moving object, that is a vector of instantaneous change of an object's position.
Let's generalize. If function h(t) represents the value of some physical characteristic as a function of time, its derivative h'(t) represents an instantaneous speed of change of this physical characteristic.
Using this logic, we can find an instantaneous speed of change of an
instantaneous speed of change, which would be a derivative of the
derivative, that is a second derivative of a base function h(t).
This is the logic behind analyzing how an instantaneous speed of change of an object's position itself changes with time.
Acceleration is an instantaneous speed of change of an
instantaneous speed of change of an object's position. By definition, it
is a vector with components equal to derivatives of corresponding
components of an instantaneous speed of change of an object's position.
Considering the latter is a vector with components equal to derivatives
of original coordinate functions, acceleration is a vector a represented by three second derivatives of the coordinate functions describing the object's position:
a = {x"(t), y"(t), z"(t)}
A short note about terminology.
We distinguished velocity (a vector) from speed (its magnitude). In case of acceleration there is no separate word to distinguish a vector of acceleration from its magnitude. Both are called acceleration, and it's the context that helps to distinguish one from another.
Usually, if the motion occurs in one dimension along a straight line in
one direction, there is no big difference between a vector and its
magnitude, and there should be no confusion. In two- and
three-dimensional cases with movement along some curve we will usually
consider acceleration as a vector.
Let's consider a few examples.
Example 1. An object is at rest at the origin of coordinates.
So, x(t)=y(t)=z(t)=0 for all time moments t.
Velocity v of this movement is null-vector for all time moments, since a derivative from a constant equals to 0.
Indeed, x'(t)=y'(t)=z'(t)=0 and
= {0, 0, 0}.
Hence, its instantaneous speed s (magnitude of the vector of velocity) is also 0.
Acceleration, similarly, is a null-vector for all time moments as well, as
= {0, 0, 0}.
Its magnitude is, obviously, 0.
Example 2. An object is at rest at a point with coordinates
So, x(t)=3; y(t)=10; z(t)=−6 for all time moments t.
Velocity v of this movement is null-vector for all time moments, since a derivative from a constant equals to 0.
Indeed, x'(t)=y'(t)=z'(t)=0 and
= {0, 0, 0}.
Hence, its instantaneous speed s (magnitude of the vector of velocity) is also 0.
Acceleration, similarly, is a null-vector for all time moments as well, as
= {0, 0, 0}.
Its magnitude is, obviously, 0.
Example 3. An object is in the uniform motion. At time t=0 it is at a point with coordinates
It moves along a straight line according to the following coordinate functions:
x(t)=3+6·t;
y(t)=10−8·t;
z(t)=−6+10·t
for all time moments t.
Velocity v is vector with the following components:
x'(t)=6; y'(t)=−8; z'(t)=10.
Therefore,
= {6, −8, 10}.
Hence, its instantaneous speed s (magnitude of the vector of velocity) is
s = √(6)²+(−8)²+(10)² = 10√2.
Acceleration is a null-vector for all time moments of time because the velocity is constant:
a = {x"(t), y"(t), z"(t)} =
= {0, 0, 0}.
The magnitude of acceleration is, obviously, 0.
Example 4. An object falls down from the Tower of Pisa, pulled by gravity, accelerating all the time. At time t=0 it is at the top of the tower at a point with coordinates
It moves along a straight line down the Z-axis towards point
x(t)=0;
y(t)=0;
z(t)=H−g·t²/2
(where g is a positive constant related to strength of the gravity)
for all time moments t.
Velocity v is vector with the following components:
x'(t)=0; y'(t)=0; z'(t)=−g·t.
Therefore,
= {0, 0, −g·t}.
Hence, its instantaneous speed s (magnitude of the vector of velocity) is
s = √(0)²+(0)²+(−g·t)² = g·t.
Acceleration a is a vector with the following components:
a = {x"(t), y"(t), z"(t)} =
= {0, 0, −g}.
The magnitude of acceleration is, obviously, g.
We can also calculate the time, when this object reaches the ground (that is, when z(t)=0). For this we just have to resolve the equation
The solution is, obviously,
Monday, April 16, 2018
Unizor - Physics4Teens - Mechanics - Kinematics - Speed, Velocity
Notes to a video lecture on http://www.unizor.com
Speed and Velocity
This is the first Physics lecture, where a solid mathematical background will be needed.
In particular, we assume the familiarity with vectors and derivatives.
These and many other mathematical concepts can be found in the course
"Math 4 Teens" on the same site as this lecture - UNIZOR.COM.
In the first approximation speed is a distance covered by a moving object in a unit of time.
What's wrong with this definition?
Firstly, a moving object moves with a different speed at different
moments in time, so speed is a function of time, which is not reflected
in this definition.
Secondly, what is a "unit of time"? Any unit of time, like a second, is
not a "moment" in time, but an interval, during which an object can
still change its speed.
Let's approach this concept more rigorously.
Our task is to define a speed as a characteristic of motion at any moment in time.
The simplest motion we consider first is a movement of an object along
the X-axis, according to the following function of X-coordinate of time t:
Let's define the average speed during any time interval from moment t1 to moment t2 as the distance covered during this time interval divided by the length of time this distance was covered.
For an object moving along the X-axis this average speed can be expressed in a formula:
save(t1, t2) =
= [x(t2) − x(t1)] / (t2 − t1)
Remarkably, the average speed for an object uniformly moving along the X-axis as
save(t1, t2) =
= [a·t2 − a·t1] / (t2 − t1) = a
Of course, this type of movement is called uniform exactly for this reason - average speed of movement is constant on any time interval.
Consider now a movement along the X-axis according to general function x(t) and the task of defining its speed at any moment t.
Let's note the position of our object at two moments in time - t and t+Δt. We can find an average speed during this time period:
save(t, t+Δt) =
= [x(t+Δt) − x(t)] / (t+Δt − t) =
= [x(t+Δt) − x(t)] / Δt
It is reasonable now to define a speed at moment t, called instantaneous speed s(t), as a limit of the above expression for the average speed on interval [t, t+Δt], when Δt is diminishing to 0, that is time increment Δt is an infinitesimal variable:
s(t) =
= limΔt→0[x(t+Δt) − x(t)] / Δt
The limit above is a definition of the derivative of a function x(t). Therefore, the rigorous definition of an instantaneous speed of an object moving along the X-axis according to function of time x(t) is the derivative of this function:
s(t) = dx(t)/dt = x'(t)
In one of the previous lectures we mentioned that coordinate functions x(t), y(t) and z(t) must be continuous to prevent instant science fiction jumps to other planets. From now on we will also assume that these coordinate functions are differentiable to be able to determine the speed of movement as a derivative of a coordinate function by time.
This completes the definition of speed for a one-dimensional movement along the X-axis.
Now we will address general case of movement in three-dimensional space described by coordinate functions x(t), y(t) and z(t).
To define a speed in case of general three-dimensional movement represented by three coordinate functions x(t), y(t) and z(t), we will use the vector representation of the position of an object.
So, assume that at time from t to t+Δt a vector a from the origin of coordinates to point
Then the difference between these vectors is a displacement that
happened with a moving object during this time. The first important
thing to notice here is that this displacement is a vector
Though we did not mention the vector character of the movement along the
X-axis above, it was implicitly there, because movements forward
(towards increasing X-coordinates) or backward (towards decreasing
X-coordinates) are two different directions that are characteristic of
vectors. So, the positive or negative displacement
Now, when we have determined the vector character of a displacement from a position a at time t to position b at time t+Δt, we can define the average displacement during this period of time - it's a vector
Coordinates of this vector are, obviously,
Δx(t) = x(t+Δt) − x(t),
Δy(t) = y(t+Δt) − y(t),
Δz(t) = z(t+Δt) − z(t).
When time increment Δt is infinitesimal, all three components of the displacement vector are infinitesimal as well.
If all three coordinate functions are differentiable (which we will always assume), the limit of the average displacement vector
Hence, the instantaneous speed of movement of an object defined by coordinate functions x(t), y(t) and z(t) is a vector with coordinates
This vector is called velocity, while the term speed is reserved only for the magnitude of this vector, that is its absolute value, disregarding the direction, which is equal to
√[x'(t)]²+[y'(t)]²+[z'(t)]²
Unizor - Physics4Teens - Mechanics - Kinematics - Space
Notes to a video lecture on http://www.unizor.com
Speed and Velocity
This is the first Physics lecture, where a solid mathematical background will be needed.
In particular, we assume the familiarity with vectors and derivatives.
These and many other mathematical concepts can be found in the course
"Math 4 Teens" on the same site as this lecture - UNIZOR.COM.
In the first approximation speed is a distance covered by a moving object in a unit of time.
What's wrong with this definition?
Firstly, a moving object moves with a different speed at different
moments in time, so speed is a function of time, which is not reflected
in this definition.
Secondly, what is a "unit of time"? Any unit of time, like a second, is
not a "moment" in time, but an interval, during which an object can
still change its speed.
Let's approach this concept more rigorously.
Our task is to define a speed as a characteristic of motion at any moment in time.
The simplest motion we consider first is a movement of an object along
the X-axis, according to the following function of X-coordinate of time t:
Let's define the average speed during any time interval from moment t1 to moment t2 as the distance covered during this time interval divided by the length of time this distance was covered.
For an object moving along the X-axis this average speed can be expressed in a formula:
save(t1, t2) =
= [x(t2) − x(t1)] / (t2 − t1)
Remarkably, the average speed for an object uniformly moving along the X-axis as
save(t1, t2) =
= [a·t2 − a·t1] / (t2 − t1) = a
Of course, this type of movement is called uniform exactly for this reason - average speed of movement is constant on any time interval.
Consider now a movement along the X-axis according to general function x(t) and the task of defining its speed at any moment t.
Let's note the position of our object at two moments in time - t and t+Δt. We can find an average speed during this time period:
save(t, t+Δt) =
= [x(t+Δt) − x(t)] / (t+Δt − t) =
= [x(t+Δt) − x(t)] / Δt
It is reasonable now to define a speed at moment t, called instantaneous speed s(t), as a limit of the above expression for the average speed on interval [t, t+Δt], when Δt is diminishing to 0, that is time increment Δt is an infinitesimal variable:
s(t) =
= limΔt→0[x(t+Δt) − x(t)] / Δt
The limit above is a definition of the derivative of a function x(t). Therefore, the rigorous definition of an instantaneous speed of an object moving along the X-axis according to function of time x(t) is the derivative of this function:
s(t) = dx(t)/dt = x'(t)
In one of the previous lectures we mentioned that coordinate functions x(t), y(t) and z(t) must be continuous to prevent instant science fiction jumps to other planets. From now on we will also assume that these coordinate functions are differentiable to be able to determine the speed of movement as a derivative of a coordinate function by time.
This completes the definition of speed for a one-dimensional movement along the X-axis.
Now we will address general case of movement in three-dimensional space described by coordinate functions x(t), y(t) and z(t).
To define a speed in case of general three-dimensional movement represented by three coordinate functions x(t), y(t) and z(t), we will use the vector representation of the position of an object.
So, assume that at time from t to t+Δt a vector a from the origin of coordinates to point
Then the difference between these vectors is a displacement that
happened with a moving object during this time. The first important
thing to notice here is that this displacement is a vector
Though we did not mention the vector character of the movement along the
X-axis above, it was implicitly there, because movements forward
(towards increasing X-coordinates) or backward (towards decreasing
X-coordinates) are two different directions that are characteristic of
vectors. So, the positive or negative displacement
Now, when we have determined the vector character of a displacement from a position a at time t to position b at time t+Δt, we can define the average displacement during this period of time - it's a vector
Coordinates of this vector are, obviously,
Δx(t) = x(t+Δt) − x(t),
Δy(t) = y(t+Δt) − y(t),
Δz(t) = z(t+Δt) − z(t).
When time increment Δt is infinitesimal, all three components of the displacement vector are infinitesimal as well.
If all three coordinate functions are differentiable (which we will always assume), the limit of the average displacement vector
Hence, the instantaneous speed of movement of an object defined by coordinate functions x(t), y(t) and z(t) is a vector with coordinates
This vector is called velocity, while the term speed is reserved only for the magnitude of this vector, that is its absolute value, disregarding the direction.
Friday, April 13, 2018
Unizor - Physics4Teens - Mechanics - Kinematics - Time
Notes to a video lecture on http://www.unizor.com
Time
Time is an undefined concept. In this way it is similar to such concepts as geometric point. It is specifically physical concept, and Physics needs this concept to quantitatively characterize the physical processes.
As is the case with any mathematical undefined concepts, we study not the concept of time itself, but its properties that we postulate.
Though time-related postulates might not seem as mathematically
rigorous as Euclidean postulates in Geometry, we will try to describe
them with utmost accuracy.
First of all, time is one of the forms of existence of the world around us, and any change in the world are related to change of time.
There are no changes in the world not related to change of time and,
from the opposite side, there is no change in time without some changes
in the world.
Using this connection between change of time and some changes in the
world around us, we can choose one particular process that occurs in our
world with relative regularity as the main time-measuring device and
measure time by changes in this process. Obviously, this process should
be stable, repetitive, regular, predictable etc. to be used as a
time-measuring device.
So, what can be used as such a process?
In the previous lecture we have suggested that the rotation of the Earth
around its axis can be used as this process. We have divided the period
of one rotation into 24 hours, each hour - into 60 minutes, each minute
- into 60 seconds, and suggested a second as the main unit of time.
In addition, classical Physics (a subject of this course) assumes (postulates, makes it an axiom) the continuity of time,
which implies that we can divide any interval of time into however
small intervals and still obtain valid time intervals, reflecting
certain changes in the world. That's why we can talk about milliseconds
(1/1000th of a second), microseconds (1/1000000th of a second) etc.
That means that we can choose any arbitrary moment of time as the beginning of time
(zero point) and use a real number of seconds since or before this
moment to any other moment of time. So, time can be measured and any
moment of time can be characterized by a real number - the number of
second since or before the beginning of time to this moment. This real
number is positive for all moments of time that characterize the
processes happened after the beginning of time and it is negative for
those that precede the beginning.
But how to determine the period of one rotation of the Earth that we
suggested as a time-measuring device? Well, we can use a telescope fixed
at some place on Earth, look at the stars and watch how they change
their location in the telescope. Obviously, they will move, as our
planet rotates, and after one rotation the stars will be in the same
position on the sky and in the telescope.
Unfortunately, this might be a good measure for technology in Ancient
Egypt, but today's necessities need more precision. So, let us describe
the contemporary time-measuring process.
Atomic clock is considered nowadays a standard for precise time
measurement. The time interval of 1 second in the International System
of Units (SI) is derived from the oscillation between two states of an
atom of an element cesium. More exactly, 1 second is a time interval
during which 9,192,631,770 oscillations occur. This clock's precision is
1 second in about 30 million years - quite sufficient for all
foreseeable needs.
For all simpler practical reasons people use the clock as a time
measuring device, periodically synchronizing it with atomic clock
through different interfaces.
We have already discussed the first axiom of time - continuity.
There is another very important time-related axiom accepted by classical
Physics. It states that physical processes behave the same, regardless
of time when they occur. In other words, an experiment conducted today
will have exactly the same outcome as an identical experiment conducted
tomorrow. In this statement the word "identical" is very important, it
means that everything involved in the experiment today must be the same
as in the tomorrow's experiment. If this rule is observed, the only
difference between experiments is the time when they are conducted, and
that must not affect the results of an experiment.
Another form of this axiom is: time is uniform.
CONCLUSION
The continuity and uniformity are properties of an abstract concept of time
that we use as the characteristic of all processes occurred in our
world. Time intervals can be measured by different kinds of clocks, the
unit of measurement accepted in the International System of Units (SI)
is a second.
Using these properties of time to define the motion, we can
always describe a motion in our three-dimensional space as three real
functions (space coordinates) x(t), y(t) and z(t) of real argument (time) t. The only thing we need is a system of Cartesian coordinates and a moment of time we choose as the beginning of motion.
Wednesday, April 11, 2018
Unizor - Physics4Teens - Mechanics - Kinematics - Trajectory
Notes to a video lecture on http://www.unizor.com
Trajectory
Trajectory is a set of all points in the three-dimensional space visited by a moving object (a point) during its motion. In other words, it's a trace of the motion.
If an object is moving, we can see its position at any moment in time.
After it has left one position in space and moved to another, the old
position is empty, we cannot see anything there, unless we leave certain
mark in space at every position visited by our object.
So, we cannot see an entire trajectory, unless we use some special
marking in our three dimensional space for each position visited by a
moving object.
For example, if our object is a tip of a pencil and its movement is
restricted to a surface of a paper, such a movement leaves a line on a
paper that represents the trajectory.
In three dimensional space it's more difficult to arrange conditions of a
motion that leaves a visible trace, but not impossible. Wilson Cloud
Chamber is an example of such an arrangement. Elementary particles
flying through it leave traces.
Now, when a concept of trajectory is introduced, let's define it more rigorously.
When talking about motion in more precise terms, we imply existence of
Cartesian coordinates with known origin, direction of axes and unit of
measurement of the length, certain time interval (usually, from 0 to some time limit T), during which the motion takes place, and coordinate functions of time x(t), y(t) and z(t), defining X-, Y- and Z-coordinates of a moving object at any moment of time t. These functions are defined on time interval [0, T], so we know the position of a moving object at any moment of time.
With that information we can define a trajectory of the movement as a set of all points with coordinates {x(t), y(t), z(t)}, where time parameter t belongs to an interval [0, T].
Obviously, the three coordinate functions x(t), y(t) and z(t) must be defined for any argument t that belongs to interval [0, T] (mathematically expressed as
We can say even more about these functions. They must be continuous,
otherwise it would appear that in zero time our object moved from one
point to another on some distance, implying its infinite speed - a dream
of science fiction.
While we have no knowledge about forces affecting the motion, we cannot
predict the trajectory. All we can do is to observe it. Knowing all the
forces and the laws describing the results of their action on a moving
object, we will be able to predict the trajectory beforehand. This will
be discussed in lectures dedicated to Dynamics later in this course.
Let's discuss certain types of trajectories we will be dealing with in this course.
Straight line trajectory is the simplest one. Describing a motion
along this line, we will usually have the X-axis directed along the
line of motion. That results in Y- and Z-coordinates of a moving object
to be equal to zero at all times, that is y(t)=0 and z(t)=0 for all
So, only one function x(t), defined for all
While qualitative analysis of function x(t) that describes certain types of straight line
movements is interesting, the reverse analysis is more fruitful from
the theoretical viewpoint. Let's examine a trajectory for a few types of
coordinate function x(t) (assuming x(0)=0 to signify that an object is at the origin of coordinates at time t=0 and two other coordinate functions, y(t) and z(t), are equal to zero for all
If x(t)=0 for all
If x(t)=a·t, the object moves along the X-axis with constant speed, that is covering a units of length (say, meters) for each unit of time (say, second).
If x(t)=a·sin(t), the object moves along the X-axis oscillating back and forth.
If x(t)=2t−1, the object moves along the X-axis
always in a positive direction with increasing speed, that is covering
greater distance in a unit of time for greater values of time t. In other words, from t=100 to t=101 the object covers greater distance than from t=10 to t=11.
Circular trajectory occurs when an object moves within certain plane in our three-dimensional space in a circle of some radius R
around some central point. An example of such a movement might be the
rotation of any point on a carousel around its center. In this case it's
convenient to choose a system of Cartesian coordinates with origin in a
center of rotation with a plane of rotation lying in the XY-plane. Then
the Z-coordinate of a moving object will always be zero and the motion
can be described by two functions x(t) and y(t), always satisfying the equation x2(t) + y2(t) = R2.
For example, these coordinate functions define a motion with circular trajectory of radius R within an XY-plane with a center at the origin of coordinates:
x(t) = R·cos(t)
y(t) = R·sin(t)
z(t) = 0
Spiral trajectory occurs when an object moves in our three-dimensional space along a cylindrical surface of some radius R,
circling around the cylinder's axis with its projection on this axis
moving always forward. An example of this motion might be the movement
of the tip of a cork screw, when you open a bottle standing on a table.
While getting down into the cork, this tip makes small circles around
the cork screw's main axis. In this case it's convenient to choose a
system of Cartesian coordinates with Z-axis going down along the axis of
rotation of a cork screw (down into the bottle along its central axis)
and XY-plane to be perpendicular to this axis (and perpendicular to a
bottle's central axis), aligned to the top of a bottle. Then the
Z-coordinate of a tip of a cork screw will be a function of time
representing the depth of the tip inside a cork. The X and Y coordinates
will be similar to those for a plain circular trajectory described above.
For example, the following coordinate functions define a motion with spiral trajectory:
x(t) = R·cos(t)
y(t) = R·sin(t)
z(t) = a·t
Obviously, the complexity of the trajectories has no limits, but in this course we will be dealing with simple ones.
Subscribe to:
Posts (Atom)

