Unizor - Derivatives - Function Limits - Exercise 3

Notes to a video lecture on http://www.unizor.com

Function Limit - Exercise
(x→a)

Try to do these exercises yourself.

All function limits below are supposed to be calculated as argument x tends to real number a.
In other words, we say that
f(x)→L as x→a, if
∀ positive ε (however small)
∃δ: (|x−a| ≤ δ) ⇒ (|f(x)−L| ≤ ε)

1. If x=a is a point of continuity for function f(x) then, as follows from the definition of continuous function,
f(x) → f(a)
Find the following limits:
3x³-2x²+x-1 as x→1
2^x as x→3
sin(x) as x→π/2
lg(10x) as x→100

2. Indeterminate 0/0 or 0·∞
(x²−4)/(x−2) as x→2
(1−cos(x))/x² as x→0
(5^x−1)]/x as x→0
sin(x)/(e^x−1) as x→0

3. Indeterminate ∞−∞
sin(x)·tan(x) − sec(x) as x→π/2
1/(x²-3x+2) − 1/(x²+5x−6)
as x→1
ln(sin(x)) − ln(x) as x→0
√x+1/(x−4) − √x+16/(2x−8)
as x→4

Unizor - Derivatives - Function Limits - Exercise 1

Notes to a video lecture on http://www.unizor.com

Function Limit - Exercise
(x→+∞)

Try to do these exercises yourself.

All function limits below are supposed to be calculated as argument x tends to positive infinity, that is infinitely increasing without bounds, eventually getting larger than any real number fixed beforehand and staying larger than that number ever since.
In other words, we say that
f(x)→L as x→+∞, if
∀ε>0 ∃A: (x ≥ A)⇒|f(x)−L| ≤ ε

Find the limits of the following functions as their argument xinfinitely increasing.

1. (2x²+3x+4)/(3x²+4x+5)
Answer: 2/3

2. (2x³+3x+4)/(3x²+4x+5)
Answer: Function will be infinitely increasing or, non-rigorously, its limit is +∞

3. (2x²+3x+4)/(3x³+4x+5)
Answer: 0

4. x·sin(1/x)
Answer: 1

5. x/3^x
Hint: Prove that n+1 ≤ 2ⁿ for all natural n and expand it to all real x ≥ 1
Answer: 0

6. x²/3^x
Hint: Prove that (n+1)² ≤ 2ⁿ for all natural n ≥ 6 and expand it to all real x ≥ 6
Answer: 0

Unizor - Derivatives - Function Limits - Exercise 2

Notes to a video lecture on http://www.unizor.com

Function Limit - Exercise
(x→−∞)

Try to do these exercises yourself.

All function limits below are supposed to be calculated as argument x tends to negative infinity, that is infinitely decreasing without bounds, eventually getting less than any real number fixed beforehand and staying below that number ever since.
In other words, we say that
f(x)→L as x→−∞, if
∀ positive ε (however small)
∃A: (x ≤ A)⇒|f(x)−L| ≤ ε

In some cases it's useful to use the following

Theorem
If f(x)→L as x→−∞,
then f(−x)→L as x→+∞
and converse (former follows from latter).

Proof
Actually, this theorem is following from a more general theorem about limit of a compounded function.
Indeed, set g(x)=−x and consider limit of functionf(g(x)) as x→+∞.

However, it might be useful to prove this theorem directly.
Given that
∀ positive ε (however small)
∃A: (x ≤ A) ⇒ |f(x)−L| ≤ ε
Choose positive ε (however small).
Let B = −A.
Let x' = −x.
For any x ≥ B
it is true that −x ≤ −B.
Therefore, x' ≤ A.
Therefore, |f(x')−L| ≤ ε
Since f(x') = f(−x),
it's true that |f(−x)−L| ≤ ε
So, we have proven that
∀ε>0 ∃B:
(x ≥ B) ⇒ |f(−x)−L| ≤ ε
That is, x→+∞ ⇒ f(−x)→L
End of proof.

Find the limits of the following functions as their argument xinfinitely decreasing.

1. (2x²+3x+4)/(3x²+4x+5)
Answer: 2/3

2. (2x³+3x+4)/(3x²+4x+5)
Answer: Function will br infinitely decreasing or, non-rigorously, its limit is −∞

3. (2x²+3x+4)/(3x³+4x+5)
Answer: 0

4. x·sin(1/x)
Answer: 1

5. x·3^x
Hint: Switch to x→+∞ and the results of corresponding exercise from a previous topic.
Answer: 0

6. x²·3^x
Hint: Switch to x→+∞ and the results of corresponding exercise from a previous topic.
Answer: 0

Unizor - Derivatives - Limit of Compound Functions

Notes to a video lecture on http://www.unizor.com

Function Limit - Compounding

The following theorem might be very useful in solving the problems with limits;

Theorem

IF
f(x) and g(x) are twocontinuous functions defined for all real arguments x AND
f(x)→L as x→r AND
g(x)→M as x→L
THEN
g(f(x))→M as x→r

Proof

Since g(x)→M as x→L
∀ positive ε (however small)
∃δ:
(|f(x)−L| ≤ δ) ⇒ |g(f(x))−M| ≤ ε

Since f(x)→L as x→r
∀ positive δ (however small)
∃γ:
(|x−r| ≤ γ) ⇒ |f(x)−L| ≤ δ

So, for any chosen ε we can always find γ such that
(|x−r| ≤ γ) ⇒ |f(x)−L| ≤ δ ⇒
⇒ |g(f(x))−M| ≤ ε
End of proof.

Notes:

1. Condition of the domain of each of these functions to be all real numbers can be reduced to a condition of the domain ofg(x) to include co-domain (set of all values) of f(x).

2. Condition of continuity of both functions is mandatory for this theorem. The proof relies on it.
An example where continuity is important is as follows
f(x) = 0 for all real x
g(x) = 0 for all real x ≠ 0 AND
g(x) = 1 for x = 0
Now
f(x)→L=0 as x→r=0
g(x)→M=0 as x→L=0
But
g(f(x))→1≠M as x→r=0

3. Limit points participating in this theorem (r, L, M) might be infinite as well. The proof will be very similar and can be left to self-study.

Examples

f(x)=1/x→0 as x→+∞
g(x)=sin(x)/x→1 as x→0
Therefore,
sin(1/x)/(1/x)→1 as x→+∞

f(x)=sin(x)/x→1 as x→0
g(x)=2^x→1 as x→0
Therefore,
2^1−sin(x)/x→1 as x→0

Unizor - Derivatives - Amazing Function Limits

Notes to a video lecture on http://www.unizor.com

Amazing Limits

There are two very important limits that require special attention and non-trivial approach to analyze.
In this lecture we present them with full proof.

Amazing Limit #1

sin(x)/x → 1 as x→0

Proof

We will prove this for angles xin the first quadrant only where x, sin(x) and tan(x) are positive, the general case trivially follows from it. Let's start from the definition of trigonometric functions using the unit circle.

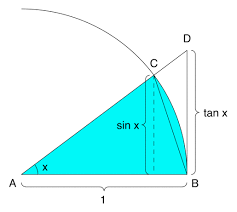
On the picture above sin x segment is an actual definition of a sine. A segment marked tan x is not a direct definition of tangent (defined as a ratio of sine to cosine), but immediately follows from it considering similar triangles ΔADB and ΔACE (point E is a base of a perpendicular from point C to X-axis, not marked on a picture).

Let's compare the areas of three geometric figures:
(a) triangle ΔACB,
(b) circular sector ACB between radiuses AC, AB and arc CB,
(c) triangle ΔADB.
Obviously,
Area(a) ≤ Area(b) ≤ Area(c)
Now let's calculate them all.

Area(a)=AB·sin(x)/2=sin(x)/2
Area(b)=πAB²x/(2π)=x/2
Area(c)=AB·tan(x)/2=tan(x)/2

Therefore,
sin(x) ≤ x ≤ tan(x)
or, since tan(x)=sin(x)/cos(x),
sin(x) ≤ x ≤ sin(x)/cos(x)

Dividing all by positive sin(x), we obtain
1 ≤ x/sin(x) ≤ 1/cos(x)
The left expression is a constant 1, the right expression tends to 1 as x→0 since cos(0)=1. Therefore, by squeeze theorem, the middle expression has a limit as x→0 and its limit is 1:
x/sin(x) → 1 as x→0
Therefore,
sin(x)/x → 1/1=1 as x→0
End of Proof.


Amazing Limit #2

(1+x)^1/x → e as x→0
where e is a fundamental constant in Calculus, approximately equal to 2.71.

Proof

First of all, we have to recall the definition of number e.

There are many definitions of e, all equivalent to each other.
In our course we have chosen the definition of e as a base of an exponential function y=e^x with steepness (which is, actually, a trigonometric tangent of a tangential line) at point x=0 being equal to 1 (that is, the tangential line at x=0 is parallel to a line y=x).

Using the terminology we are now familiar with, the steepness of a curve that represents the graph of a real function y=f(x)or, simply, the steepness of a real function y=f(x) at some point x=r is a limit of the ratio
[f(r+d)−f(r)]/d as d→0.

So, we can say that defining characteristic of number e is lim_x→0[(e^x−1)/x] = 1

Let's approach this from the position of a function graphs.
The graph of a function y = e^x−1 (which is a graph of function y = e^x shifted down by a unit) is going through the origin of coordinates and at this point, according to a definition of a constant e, its tangent coincides with the graph of function y = x.



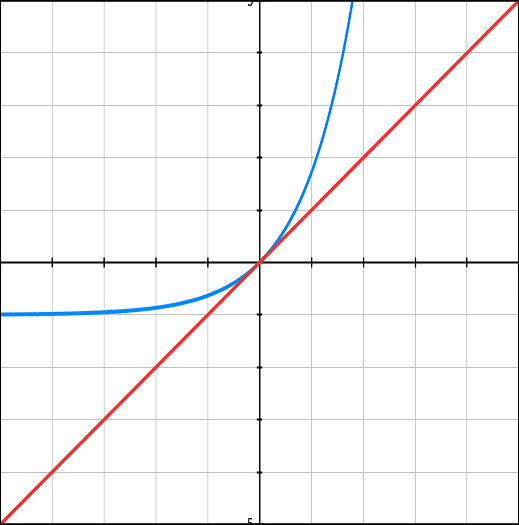
Let's analyze now the meaning of the limit we have to prove.
First of all, let's recall that, if f(x) is a continuous function and x→r, then f(x)→f(r) - this is, actually, a definition of a continuous function.
Next, it can be proven that functions e^x and ln(x) (a natural logarithm - a logarithm with a base e - log_e(x)) are continuous.
Therefore, instead of proving the limit
(1+x)^1/x → e as x→0,
we can prove that
ln(1+x)^1/x → ln(e) as x→0

Simple transformation results in the following formulation of our theorem.
Prove that
ln(1+x)/x → 1 as x→0
Let's draw a graph of ln(1+x)near point x=0 and compare it with a graph of function y=x.



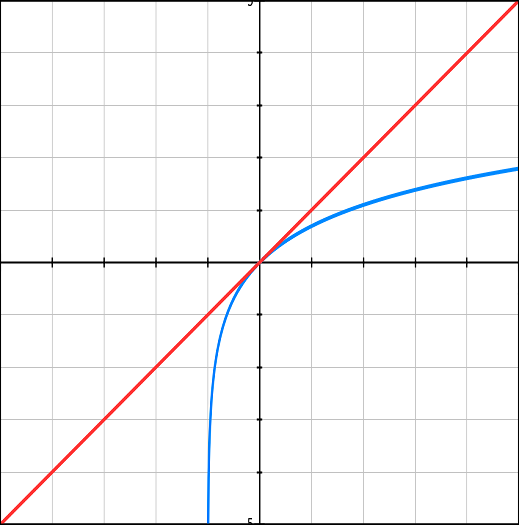
Notice that function y=ln(1+x)is inverse relative to function y=e^x−1. Here is why:
y=e^x−1 ⇒
⇒ y+1=e^x ⇒
⇒ ln(y+1)=x
so, an inverse function is y=ln(1+x).

As we know, an inverse function has a graph symmetrical to the original one relative to an angle bisector of the main coordinate angle.
This implies that, if the line y=xis tangential to a graph of function y=e^x−1 at point x=0 (which is the origin of coordinates because y=e⁰−1=0 as well), the line symmetrical to this tangential line should be tangential to a graph of function y=ln(x+1) at a point symmetrical to the origin of coordinates.

But the tangential line y=x is the angle bisector and is the axis of symmetry, so its symmetrical is itself.
Also, a point symmetrical to the origin of coordinates is itself.
So, we have that the same line y=x is tangential to both y=e^x−1 and y=ln(x+1) at the same point, which proves that
[ln(1+x)−ln(1+0)]/x → 1
as x→0.

We know that ln(1)=0. Therefore, the last expression is simplified into
ln(1+x)/x → 1 as x→0.

This completes the analysis of a problem. We are ready now to prove the original theorem.
Let's start from the last statement that we have proven using the considerations of symmetry between the original function y=e^x−1 and its inverse y=ln(1+x), that is:
ln(1+x)/x → 1 as x→0.
Let's transform it into an equivalent form using the property of logarithm log(a^b)=b·log(a) into the following:
ln((1+x)^1/x) → 1 as x→0.
Using continuity of a function e^x, apply it to the above statement:
(1+x)^1/x → e¹ as x→0.
Since e¹=e, we have the original statement proven:
(1+x)^1/x → e as x→0.
End of proof.

A simple consequence of this limit is that
(1+1/n)ⁿ → e as n→∞
since 1/n → 0 as n→∞

Unizor - Derivatives - Function Limit - Continuity

Notes to a video lecture on http://www.unizor.com

Continuous Functions

A special type of functions is widely used in mathematics. They are called continuous functions.

Simply speaking, the graph of these functions can be drawn in one movement of a pen without lifting it from the paper.
Our purpose is to define these functions more precisely, more rigorously, in order to use the term "continuous function" wherever necessary without getting into details, properties and characteristics.

The action of drawing a graph without lifting a pen from paper implies, first of all, that the graph is a line. It's not necessarily straight, it might be curved, but it is contiguous, which means that the function is defined on some contiguous interval, finite or infinite to +∞and/or −∞.
We can say now that the domain of a continuous function is a contiguous interval, finite or infinite. Here are examples of the possible domains:
[a,b]
(a,b]
[a,+∞)
(−∞,+∞)
etc.

Let's now define the action of "not lifting a pen" mathematically.
In more precise terms it means that for two points on the graph of a function y=f(x),
{x₁,y₁=f(x₁)} and
{x₂,y₂=f(x₂)},
if x₁ is close to x₂,
then y₁ will be close to y₂.
And the "closeness" should be understood in a sense ofinfinitesimal distance, that is,
if x₁→x₂ then f(x₁)→f(x₂).

It is important that this rule must be true for any point within the domain of a function, which leads us to the following more rigorous definition of a continuous function.

The real function f(x) is called continuous if
(1) its domain is a contiguous interval, finite or infinite;
(2) for any point r within its domain it is true that
if x→r, then f(x)→f(a)

The rule (2) above means, usingε-δ language, that
for any positive ε exists δ such that,
if |x−r| ≤ δ,
then |f(x)−f(r)| ≤ ε

Problems

1. Prove that f(x)=x³ is continuous.

Proof

This function is defined on a contiguous interval (−∞,+∞).
Choose any real number r and any positive ε.
Notice that
|x³−r³| = |x−r|·|x²+xr+r²| ≤
≤ |x−r|·(|x²|+|x|·|r|+|r²|)

To make the right side smaller than ε it is sufficient to chooseδ smaller than the minimum among δ₁=|r| (in which case |x|is not greater than 2|r| and the expression in parenthesis is not greater than 7r²) and δ₂=ε/(7r²)(in which case an entire right hand side of this inequality is not greater than ε).

2. Prove that f(x)=sin(x) is continuous.

Proof

This function is defined on a contiguous interval (−∞,+∞).
Choose any real number r and any positive ε.
Notice that
|sin(x)−sin(r)| =
= 2|sin((x−r)/2)·cos((x+r)/2)| ≤
≤ |x−r|

So, to make |sin(x)−sin(r)|smaller than ε, it is sufficient to chose δ=ε.

3. Let's define the following function:
f(x)=0 for all real x, except x=0and f(x)=1 for x=0.
Prove that it is not continuous.

Proof

This function is defined on a contiguous interval (−∞,+∞). So, the first requirement ofcontinuity is satisfied.
The second requirement, however, is not satisfied forr=0.
Indeed, the function f(x) has limit 0 when x approaching point 0 because all its values outside of point x=0 are equal to 0, but f(0)=1.
So, f(x) does not tend to f(0) as x→0.

Unizor - Derivatives - Function Limit - Steepness and const e

Notes to a video lecture on http://www.unizor.com

Steepness and Constant e

Another important concept we will be dealing with is a concept of a steepness of a curve that represents the graph of a real function y=f(x).

The concept of steepness of a curve at some point was introduced first in the chapter of Algebra dedicated to exponential functions. We have defined it, approximately, as a ratio of the increment of the Y-coordinate along the curve to an increment of the X-coordinate as we step forward from the original point where we want to measure the steepness.

We have also indicated that the smaller increment ofX-coordinate (that is, the closer the next point on a curve lies to the point where we measure thesteepness) - the better our approximation would be.

Using the terminology we are now familiar with, the steepnessof a curve that represents the graph of a real function y=f(x)or, simply, the steepness of a real function y=f(x) at some point x=r is a limit of the ratio of f(r+d)−f(r) to d as d→0,
that is,
lim_d→0[f(r+d)−f(r)] /d

When we introduced the exponential functions y=a^x in the chapter "Algebra - Exponential Function", we have proven that the steepness of function y=a^x at point x=0depends on the value of its basea, and, for a=2 the steepness of function y=2^x is less than 1, while for a=3 the steepness of function y=3^x is greater than 1.

Assuming that the steepness is smoothly increasing, as we increase the base from a=2 toa=3, it is reasonably to assume the existence of such base between these two values, for which the steepness at pointx=0 is equal exactly to 1.

This value, obviously, is not an integer and, as can be proven, not even rational. Traditionally it is designated by the letter e(probably, in honor of a famous mathematician Euler who extensively researched its properties) and is considered as a fundamental mathematical constant, like π.
The approximate value of this constant is 2.71.

Now we can state that
lim_d→0[e^r+d−e^r] /d = 1

The above can be accepted as a definition of a number e. There are a few others, all equivalent to this one, that is each definition can be proven based on another definition.
Here are a few.
lim_n→∞(1+1/n)ⁿ = e
lim_d→0(1+d)^1/d = e
lim_n→∞[n·(n!)^-1/n] = e
lim_n→∞(1/0!+1/1!+...+1/n!) = e
The last one can be formulated using infinite summation sign as
Σ^∞_n=0(1/n!) = e

In this course we will assume the definition of number e as a base of an exponential functiony=e^x that has a steepness of 1 at point x=0.

It means that we consider as given the following statement, constituting the defining property of number e.

For any, however small, positive ε exists δ such that
IF |d| ≤ δ
THEN |(e^d−e⁰)/d − 1| ≤ ε
or, considering e⁰=1,
|(e^d−1)/d − 1| ≤ ε

For those math purists, the existence and uniqueness of this number e was not rigorously addressed. We just relied on the monotonic smoothness ofsteepness of an exponential function y=a^x at point x=0 as we increase the base from a=2, when this steepness is less than1, to a=3, when it is greater than 1.

Unizor - Derivatives - Function Limit - Squeeze Theorem

Notes to a video lecture on http://www.unizor.com

Squeeze Theorem

In this lecture we present a very important so-called "Squeeze Theorem" for function limits, which we did prove for sequences before.

Squeeze Theorem
(also known as
"Pinching Theorem" or
"Sandwich Theorem", or
"Theorem about Two Policemen and a Drunk")

IF, when
x→r or x→+∞, or x→−∞,
it is GIVEN that
f(x)→L AND
h(x)→L AND
f(x) ≤ g(x) ≤ h(x)
THEN
(under the same condition of tendency of argument x)
IT IS TRUE that
g(x)→L

The variant of this theorem is when L is not a concrete real number, but can be (non-rigorously) positive or negativeinfinity or (more rigorously) both functions f(x) and h(x) can be infinitely increasing or infinitely decreasing.

Proof

Let's prove for x→r where r - any real number. The other two conditions, when x→+∞ or x→−∞, or cases, when the limit is infinite, will not present any problem as a self-study exercise, they are, generally speaking, similar to the proof below.
We will use ε-δ definition of a limit.

Fix any positive ε. We have to find δ such that, if |x−r| ≤ δ, then |g(x)−L| ≤ ε.

For this ε we can find δ₁ such that in δ₁-neighborhood of x=rit is true that
|f(x)−L| ≤ ε or, equivalently,
L−ε ≤ f(x) ≤ L+ε

For the same ε we can find δ₂such that in δ₂-neighborhood ofx=r it is true that
|h(x)−L| ≤ ε or, equivalently,
L−ε ≤ h(x) ≤ L+ε

Now choose δ equal to a minimum among δ₁ and δ₂. Obviously, in δ-neighborhoodof x=r it is true that
L−ε ≤ f(x) ≤ L+ε AND
L−ε ≤ h(x) ≤ L+ε

Therefore, in thisδ-neighborhood of x=r it is true that
L−ε ≤ f(x) ≤ g(x) ≤ h(x) ≤ L+ε
Hence, |g(x) − L| ≤ ε
End of Proof.

Unizor - Derivatives - Function Limits - Standard Problems

Notes to a video lecture on http://www.unizor.com


Function Limit -
Standard Problems

Let's recall two definitions of a limit of function.

Definition 1
Value a is a limit of functionf(x) when its argument xconverges to real number r, if for ANY sequence of argument values {x_n} converging to r the sequence of function values {f(x_n)} converges to a.
Symbolically:
∀{x_n}→r ⇒ {f(x_n}→a

Definition 2
For any positive ε there should be positive δ such that, if x is withinδ-neighborhood of r (that is,|x−r| ≤ δ), then f(x) will be within ε-neighborhood of a(that is, |f(x)−a| ≤ ε).
Symbolically:
∀ ε>0 ∃ δ>0:
|x−r| ≤ δ ⇒ |f(x)−a| ≤ ε

Solving the problems below, you can use any of these definitions to prove the existence of a limit and to find its concrete value.

Problem 1

Consider a function defined for all real arguments x and δ:
f(x) = [(x+δ)²−x²] / δ
Assume that variable x is fixed, while variable δ converges to 0.
Prove that this function has a limit for δ→0 and that this limit equals to 2x.

Solution 

[(x+δ)²−x²] / δ =
= (x+δ−x)·(x+δ+x) / δ =
= δ·(2x+δ) / δ =
= 2x+δ
which converges to 2x as δ→0

Problem 2

Consider a function defined for all real arguments x and δ:
f(x) = [(x+δ)ⁿ−xⁿ] / δ
Assume that variable x is fixed, while variable δ converges to 0.
Prove that this function has a limit for δ→0 and that this limit equals to n·xⁿ⁻¹.

Solution 

[(x+δ)ⁿ−xⁿ] / δ =
= (x+δ−x)·
·[Σ_{j∈[0,n−1]}(x+δ)^n−1−j(x)^j] / δ =
= Σ_{j∈[0,n−1]}(x+δ)^n−1−j(x)^j
which converges to
= Σ_{j∈[0,n−1]}(x)^n−1−j(x)^j =
= n·xⁿ⁻¹

Problem 3

For this problem you will need a theorem proven in theTrigonometry chapter (see lecture Geometry with Trigonometry - Lim sin(x)/x) that states that
sin(δ)/δ→1 if δ→0.

Consider a function defined for all real arguments x and δ:
f(x) = [sin(x+δ)−sin(x)] / δ
Assume that variable x is fixed, while variable δ converges to 0.
Prove that this function has a limit for δ→0 and that this limit equals to cos(x).

Solution 

f(x) = [sin(x+δ)−sin(x)] / δ =
= (1/δ)[sin(x)cos(δ) +
+ cos(x)sin(δ)−sin(x)] =
= cos(x)·[sin(δ)/δ] −
− sin(x)·[1−cos(δ)]/δ

As we know, if δ→0,
sin(δ)/δ→1.
Therefore, the first component of the above expression is converging as follows
cos(x)·[sin(δ)/δ]→cos(x)

Considering
1−cos(δ) = 2sin²(δ/2),
we can write the following expressions:
[1−cos(δ)]/δ = 2sin²(δ/2)/δ =
= sin(δ/2)·[sin(δ/2)/(δ/2)]

The product of infinitesimal function sin(δ/2) (as δ→0) and a function sin(δ/2)/(δ/2)converging to 1 results in infinitesimal function.

Therefore,
sin(x)·[1−cos(δ)]/δ
is infinitesimal as δ→0 and our original function converges tocos(x)

Problem 4

Consider a function defined for all real arguments x and δ:
f(x) = [cos(x+δ)−cos(x)] / δ
Assume that variable x is fixed, while variable δ converges to 0.
Prove that this function has a limit for δ→0 and that this limit equals to −sin(x).

Solution 

f(x) = [cos(x+δ)−cos(x)] / δ =
= (1/δ)[cos(x)cos(δ) −
− sin(x)sin(δ)−cos(x)] =
= −sin(x)·[sin(δ)/δ] −
− cos(x)·[1−cos(δ)]/δ

As we know, if δ→0,
sin(δ)/δ→1.
Therefore, the first component of the above expression is converging as follows
−sin(x)·[sin(δ)/δ]→−sin(x)

Considering
1−cos(δ) = 2sin²(δ/2),
we can write the following expressions:
[1−cos(δ)]/δ = 2sin²(δ/2)/δ =
= sin(δ/2)·[sin(δ/2)/(δ/2)]

The product of infinitesimal function sin(δ/2) (as δ→0) and a function sin(δ/2)/(δ/2)converging to 1 results in infinitesimal function.

Therefore,
cos(x)·[1−cos(δ)]/δ
is infinitesimal as δ→0 and our original function converges to−sin(x).

Problem 5

Consider a function defined for all non-negative arguments xand δ:
f(x) = [√(x+δ)−√x] / δ
Assume that variable x is fixed, while variable δ converges to 0.
Prove that this function has a limit for δ→0 and that this limit equals to 1/(2√x).

Solution 

Multiply numerator and denominator of the original function by [√(x+δ)+√x].
The numerator will become[(x+δ)−x]=δ and it can be canceled with δ in denominator.
The result is
1 / [√(x+δ)+√x],
which converges to 1/(2√x) asδ→0.