Unizor - Physics4Teens - Energy - Heat Transfer - Radiation

Notes to a video lecture on http://www.unizor.com

Heat Transfer - Radiation

Heat radiation IS NOT the same as radioactivity. Though, under certain circumstances (like an explosion of an atomic bomb) the heat radiation and radioactivity are both present. When we discuss the heat radiation we talk about a process that occurs in any object with a temperature greater than absolute zero, while radioactivity occurs in extreme cases of very high energy output.

Heat transfer through radiation is totally different from conduction and convection. The most important property of heat transfer by radiation is that heat transfer occurs without any visible material conduit that carries the heat, like molecular movement in two other cases.

Let's start from an example.
The brightest example is our Sun, as a source of heat energy. Between Sun and Earth there is no visible material conduit, yet the heat comes to Earth and is a source of life on our planet.

The fundamental concept that lies in the foundation of a process of heat radiation is a concept of a field.
The field is a region of space, where certain forces act on certain objects without visible material medium.
As an example of the field, consider gravity. The Sun keeps planets on their orbits, the Earth keeps the Moon circling around, people are walking on the ground without flying away to stars etc. We did not know much about WHY the gravitational field exist, yet we did study its behavior, the forces involved and the laws of motion in this field.

There are other fields.
Magnetic field around our planet, acting on a compass, forces the arrow to point North.
Electric field exists around electrically charged objects, so other electrically charged objects are attracted to or repulsed from it.

In Physics we successfully study these fields, but complete understanding of WHY they have the properties that we observed is not completely clear. So, we will concentrate on properties, answering the question HOW?, not on a more fundamental question WHY?.

Let's start with a particular field called electro-magnetic. Very simplified description of this field is as follows.

Any electron creates an electric field around itself. Moving electrons, which we call electric current or electric field that changes in time, also create a magnetic field around them. So, changing in time electric field creates magnetic field that changes in space. It's an experimental fact, and we have the whole theory about properties of these fields.

Consider an experiment, when you move a metal rod or any other electrical conductor in a magnetic field or change a magnetic field around any electrical conductor, thus creating a magnetic field that changes in time. You will observe that there is an electric current in the conductor, thus creating an electric field that changes in space. It's an experimental fact, and we also have the whole theory about properties of this process.

So, electric field creates magnetic field, which, in turn, creates electric field etc. This is a loop of energy conversion that propagates extremely fast, with a speed of light, about 3·10⁸m/sec.

The combination of electric and magnetic forces form electro-magnetic field that propagates much faster than its physical medium - electrons. So, the propagation of the electro-magnetic field seems to be a self-sufficient process, occurring without the medium. This is a very brief and unsatisfactory explanation of the nature of the electro-magnetic field. We will not go much further in this explanation, but rather concentrate on the properties of the electro-magnetic field.

Assuming that we accept the existence of the electro-magnetic field and, however uncomfortably we feel about it, but accept that there is no need for a medium to propagate this field, we can talk about frequency of electro-magnetic transformations, that can be considered similar to oscillation of molecules in a solid. Inasmuch as the oscillations of molecules in a metal are propagated, thus transferring heat energy from hot area to cold one, oscillations of the electric and magnetic components of the electro-magnetic field transfers energy.
This energy transfer by electro-magnetic field is called radiation.

As in a case of oscillating molecules in a solid, carrying more heat energy when oscillation is more intense (higher frequency), the electro-magnetic field oscillation carries energy with higher frequencies being more "energetic" than lower.

Interestingly, receptors in our skin feel the temperature of a solid object, that is, we feel the intensity of oscillation of its molecules. Similarly, we feel the warm rays of Sun on our skin, that is, we feel the intensity of electro-magnetic oscillation of the electro-magnetic field.
What's more remarkable, we see the light. Apparently, electro-magnetic oscillations in certain frequency range act upon censors in our eyes, thus we see the light. Moreover, in this visible range of frequencies different frequencies of electro-magnetic oscillation produce effect of different colors in our eyes.

As you see, the light and heat of radiation have the same source - the oscillation of electro-magnetic field, the only difference is the frequency. In other words, the light and heat radiation are manifestations of the same process of transferring energy by the oscillations of the components of the electro-magnetic field.

An object does not have to have a temperature of the Sun to emit heat radiation. All objects that have temperature higher than absolute zero emit thermal radiation of some frequencies. Usually, the whole spectrum of frequencies of electro-magnetic oscillations is emitted by objects. Lower frequencies (usually called infrared) are felt by skin receptors, higher frequencies are visible by an eye. Frequencies higher than those visible by a human eye are called ultraviolet. Even higher frequencies are called X-rays, which can be produced by special equipment and, depending on intensity and time of exposure, can represent a health hazard. Even higher intensity and high frequencies are called gamma rays, and they are produced in extreme cases like nuclear explosion or nuclear reactor meltdown, and they are extremely dangerous and are usually meant, when the term radioactivity is used. All frequencies can be observed using some scientific instruments.

Any object, placed in the outer space will emit its heat energy through radiation until its temperature will reach absolute zero. Our Sun emits huge amounts of energy in all spectrum of frequencies in all directions and, eventually, run out of heat energy and go dark.

The intensity of radiation, that is amount of heat radiated per unit of time per unit of area of an object depends, as in other cases of heat transfer, on the temperature of an object and temperature of surrounding environment.
In the complete vacuum with no other source of energy the radiation intensity of an object is proportional to the fourth degree of its absolute temperature in °K:
q = σ·T⁴ where
σ = 5.67·10⁻⁸ W/(m²·°K⁴)
is the Stefan-Boltzmann constant.
This is the Law of Stefan-Boltzmann. Its derivation is complex and is outside of the scope of this course.

Radiation is not only emitted by objects with temperatures above absolute zero, but also can be absorbed by them and even reflected. While ability to absorb the heat is common for other heat transfer types (conduction and convection), reflection is a specific property of heat radiation. More precisely, it's a specific property of oscillations of the electro-magnetic field.
Obvious application of this property is the usage of mirrors that reflect the oscillations of the electro-magnetic field in a very broad spectrum of frequencies, including the visible light.
An example of absorbed radiation is a slice of bread toasted in the electric toaster. It absorbs the thermal radiation emitted by electric coils, that changes the bread's structure.

Unizor - Physics4Teens - Energy - Heat Transfer - Convection

Notes to a video lecture on http://www.unizor.com

Heat Transfer - Convection

As in a case of conduction, we start with a statement: heat is a form of internal energy that is related to molecular movement.
However, while heat transfer during the process of conduction occurs between molecules oscillating around their relatively fixed positions and transferring their internal energy by "shaking" the neighboring molecules, convection occurs when molecules are free to travel in different directions and carry their internal energy with them.

In other words, conduction is a pure transfer of energy on a micro level from one oscillating molecule in a relatively fixed position to another such molecule, while convectionoccurs when molecules freely fly away from their positions, carrying their internal energy with themselves, thus transferring energy on a macro level.

It should be noted that, when dealing with solid objects, conduction is a prevailing way of heat transfer, while in liquids and gases the main way of heat transfer is convection. It does not mean that conduction does not occur in liquids or gases, it does, but it does not constitute the major way of heat transfer. Much more heat is transferred through the mechanism of convection

Here are a few examples of heat transfer through convection:
(a) heating up water in a pot; heat is carried from hot bottom of a pot up by hot (fast moving with high kinetic energy) molecules;
(b) circulation of air in the atmosphere from hot places to cold;
(c) circulation of water in oceans from hot places to cold.

Describing convectionmathematically is not a simple task.
While in case of conduction we can use a relatively simple Fourier's Law of Thermal Conduction
q(x) = −k·dT(x)/dx
that describes the heat flow as a function of how fast the temperature between the layers of conducting material changes (dT(x)/dx) and properties of the material itself (conductivity coefficient k), the process of convection is significantly more complex, described by convection-diffusion differential equations that are beyond the scope of this course.

However, for practical purposes we can use a similar formula that puts the amount of heat transferred by convectionprocess in a liquid or gas during a unit of time through a unit of area as proportional to a difference of temperatures between the layers of liquid or gas and a convective heat transfer coefficient h that depends on the physical properties of this liquid or gas:
q = −h·(T₂−T₁)

This formula puts amount of heat q going through a layer of a unit area of liquid or gas during a unit of time as proportional to a difference of temperatures between bounding surfaces of this layer T₂−T₁ and some physical properties of liquid or gas expressed in convective heat transfer coefficient h that, in turn, depend on such properties as viscosity, density, the type of flow (turbulent or laminar) etc.

Consider an example.
A round steam pipe of temperature 100°C goes through a room with air temperature 25°C. We have to calculate the amount of heat from the pipe to select an air conditioner required to neutralize the heat from a pipe and keep the room temperature at that level.
Assume that the pipe's length is 4m, diameter 0.2m and the convective heat transfer coefficient of air is 40J/(sec·m²·°C). As we know, J/sec is a unit called "watt", so we will use W instead of J/sec.

The heat transfer per unit of time through a unit of area of a pipe is, therefore,
q = 40·(100−25) = 3000(W/m²)
The pipe's area is
A = π·0.2·4 = 2.512(m²)
Therefore, the pipe is producing the following amount of heat:
Q = 3000·2.512 = 7536(W)

So, we need an air conditioner that can extract 7536W of heat from the room to maintain stable temperature of 25°C.
Usually, the power of air conditioners is measured in BTU/hr (1 watt = 3.41 BTU/hr). So we need an air conditioner of approximately 2200 BTU/hr - a relatively small one.

Another example.
Outside temperature is 40°C, inside a room we want temperature 25°C. The glass wall between a room and outside air has an area of 20m². What kind of air conditioner is needed to maintain the room temperature at 25°C, assuming the convective heat transfer coefficient of air is 40W/(m²·°C)?

Q = 40·(40−25)·20 = 12000(W)
This is equivalent to about 3500 BTU/hr.

Unizor - Physics4Teens - Energy - Heat Transfer - Conduction

Notes to a video lecture on http://www.unizor.com

Heat Transfer - Conduction

As we know, heat is a form of internal energy that is related to molecular movement.

For solids the molecular movement is usually restricted to molecules' oscillation around some neutral positions.

For liquids the freedom of molecular motion is greater, but still restricted by external forces, like gravity, and surface tension. The average distance between molecules of liquids is relatively constant.

Gas molecules are usually taking all the space available for them. Such forces as gravity also restrict their movement (otherwise, the air molecules would fly away from our planet), but still allow substantial freedom. The average distance between molecules of gas mostly depends on a reservoir the gas is in, the larger the reservoir - the larger average distance between molecules.

Transfer of heat is transfer of molecular movement from one object or part of an object to another object or part of an object, from an object or part of an object with more intense molecular movement (relatively warmer) to an object or part of an object with less intense movement (relatively cooler).

There are three major ways to transfer heat from a hot object to a cold one:
Conduction,
Convection,
Radiation.
This lecture explains a concept of conduction.

Conduction

Conduction of heat energy is a transfer of molecular movement mostly applicable to solid objects - between two solid objects that touch each other, having an area of a contact, or within one object, one part of it having different temperature than another.
The conductivity is present in heat transfer in liquids and gases, but there it's usually combined with another form of heat transfer - convection, while in solids it's not the case, and we can study conductivity by itself.

An example is a building wall, one side of which towards the outside having temperature of the air outside, while inner surface of the wall having room temperature. The heat energy constantly flows from a warmer surface of the wall to the opposite cooler one with some rate of flow that depends on the thermal conductivity of the wall material. The wall material with higher level of thermal conductivity will transfer more heat energy to a cooler side within unit of time per unit of area, which is usually not a desirable property of the building walls.

The mechanism of heat transfer through conductivity can be explained as follows.
Imagine two objects (or two parts of the same object), a hot one with higher intensity of molecular movement and a cold one with lower intensity level of molecular movement, that touch each other along some surface, while completely insulated from heat around them. For example, you put a cold metal spoon into a styrofoam cup with hot tea.

Molecules of a hot object are hitting the molecules of a cold one, thus forcing the molecules of a cold object to move faster. These faster molecules of a cold object, in turn, hit their neighbors, forcing them to move faster. This process of transferring heat energy through contacting surfaces continues until the intensity of molecular movement gradually equalizes on average. A hot object will lose some energy of molecular movement, while a cold one will gain it. As a result, the temperatures of both will equalize.

Since the heat energy is a kinetic energy of molecular movement, that is a sort of mechanical energy, we expect that the total amount of energy for an isolated system will remain constant, whatever a hot object loses in its kinetic energy of molecular movement will be gained by a cold object. The total amount of heat energy will remain the same.

If you put a silver spoon into a cup of hot tea, it will heat up faster than a spoon made of steel, which, in turn, will heat up much faster then a spoon made of wood. The reason for this is that the thermal conductivity of different materials is different.

We can experimentally measure the thermal conductivity of different solids by having a standard rod of any solid material at certain starting temperature and heating its one end by bringing it to contact with some hot object. Measuring the temperature on the other end after different time intervals will give us a picture of growing temperature.

Some materials with higher thermal conductivity will have the temperature at the opposite end of a rod growing faster than in case of other materials.
Metals have much higher heat conductivity then plastic or wood, for example. That's why the handle of a tea kettle is usually made of plastic or wood. Diamonds have one of the highest thermal conductivity, even higher than silver.

More precise definition of thermal conductivity is related to a concept of heat flux(sometimes, called heat flow density or thermal flux, or thermal flow density). Heat flux is an amount of heat energy flowing through a unit of area during a unit of time.

Let's examine how heat flows through a building wall made of some uniform material from a warm room to cold air outside the building.
Assume, the room temperature is T_room and the cold air outside the building has temperature T_air . If the thickness of a wall is L, the temperature inside the wall T(x), as a function of the distance x from the surface facing outside, gradually changes from T(0)=T_air to T(L)=T_room.

It is intuitively understandable and experimentally confirmed that amount of heat energy flowing through a unit of area of such a wall during a unit of time (heat conductivity of a wall) is proportional to a difference between temperatures T_roomand T_air and inversely proportional to a thickness of a wall L:
q = −k·(T_room − T_air ) / L
(negative sign is used because the flow of heat is opposite to a direction of temperature growth).

The situation with heat fluxmight be compared with a water flow down a river between two points A and B. The difference in levels above the sea level of these points is similar to a difference in temperature between the inside and outside walls of a building. The distance between points A and B is similar to a thickness of a wall. It's reasonable to assume that amount of water flowing through a unit of area in a unit of time will be proportional to a difference between the levels of points A and B above the sea level and inversely proportional to a distance between these two points.

To make this definition of the heat flux more precise and independent of the way how the heat flows inside the wall, let's consider a thin slice of wall parallel to both sides from a point at distance x from the outdoor cold side to a point at distance x+Δx.
The heat flow through this thin slice of a wall, as a function of distance x, can be expressed similarly to the above:
q(x)=−k·[T(x+Δx)−T(x)] /Δx

Next step is, obviously, to reduce the thickness of the slice by making Δx infinitesimal, that is Δx→0, which leads to the following definition of the heat flux:
q(x) = −k·dT(x)/dx
This definition was formulated by Fourier in 1822 and is called Fourier's law of thermal conduction.
The coefficient k is called thermal conductivity.

To find the amount of heat Q(x,A) going through an area Aat distance x from the outside wall during a unit of time, we have to multiply the heat flux by an area:
Q(x,A) = −k·A·dT(x)/dx
As in a case of water flow along the river, if the temperature is linearly dependent on the distance from the outside wall, the derivative is constant and the flow of heat is constant. But, if the wall material is uneven, like in case of a river bed not being a straight line down, the heat flow rate will change.

Unizor - Physics4Teens - Energy - Measuring Heat - Problems

Notes to a video lecture on http://www.unizor.com

Measuring Heat - Problems

Problem 1

How much heat energy is required to raise the temperature of 1 kg of water from 20°C to a boiling point of 100°C?
Assume the specific heat capacity of water is
C_w = 4184 J/(kg·°C).

Answer
Q = C·m·(T_end−T_beg) =
= 4184·1·(100−20) =
= 334,720 J

Problem 2

A piece of unknown metal of mass M_m and temperature T_m was put into an isolated reservoir filled with M_w mass of water at temperature T_w. After the system of water and metal came to thermal equilibrium, its temperature became T.
Assume that the metal is not too hot (so, water will not vaporize) and not too cold (so, the water will not freeze).
Assuming that the water's specific heat capacity is known and equals to C_w, what is the specific heat capacity C_m of the unknown metal?

Answer

C_w·M_w·(T−T_w) =
= C_m·M_m·(T_m−T)
from which C_m equals to
C_w·M_w·(T−T_w)/[M_m·(T_m−T)]

Problem 3

A burger has about 300 kcal of energy in it.
1 kcal = 4184 J.
A person, who ate it, wants to spend this energy by climbing up the stairs. A person's mass is 75 kg, the height between the floor is 3 m.
Assume that only 25% of energy in the food can be used for climbing, while the other 75% is needed to maintain our body's internal functions.
Counting from the ground floor as floor #0, to what floor can a person climb using that energy from a burger?

Answer
E_bur = 300kcal · 4184J/kcal =
= 1,255,200J
E_climb = 0.25·E_bur =
= 313,800J
E_floor = 75kg · 9.8m/sec² · 3m =
= 2205J
N = E_climb / E_floor ≅ 142 floors

Problem 4

An ice of mass 0.1kg has temperature −10°C.
What's the minimum amount of water M at temperature 20°C needed to melt it?
Assume, specific heat capacity of water is 4183J/(kg·°C) and that of ice is 2090J/(kg·°C). Assume also that the amount needed to melt ice at 0°C is 333,000J/kg.

Answer
E_warm = 2090·0.1·10 = 2090J
E_melt = 333000·0.1 = 33300J
E_need = 2090 + 33300 = 35390J
E_water = 4183·M·20 = 83660·M
E_water = E_need
35390 = 83660·M
M = 0.423kg

Unizor - Physics4Teens - Energy - Heat - Heat & Temperature

Notes to a video lecture on http://www.unizor.com

Heat and Temperature

Specific Heat Capacity

Let's discuss the relationship between heat and temperature.
From the unscientific standpoint these two concepts are almost identical. Heating an object results in increase of its temperature. Increasing a temperature of an object constitutes its heating.
Yet, from the strictly scientific viewpoint these two concepts are different.

Heat is energy of some specific type, that can be transferred from one object to another, while temperature is an average kinetic energy of molecules of an object.
The same amount of heat, transferred into different objects, will result in different growth of their temperatures, depending on many factors, like mass, chemical composition, state etc. of these objects. Analogy of this is that same amount of fuel in different cars results in achieving very different speeds and, therefore, different kinetic energies in different cars, even if the gas pedal is pushed all the way down for all cars. It's just because cars are different and their internal structure converts fuel into movement differently.

It has been experimentally observed that to increase a temperature of an isolated object of a unit mass by a unit of temperature is independent (within reasonable level of precision) of the initial temperature of an object, but depends only on the type of object's material, composition, state etc. In other words, amount of heat needed to increase a temperature of 1 kg of water from 20°C to 21°C is the same as from 50°C to 51°C. If, instead of water, we take copper, the amount of heat, needed to increase its temperature from 20°C to 21°C, will be the same as to increase it from 50°C to 51°C, but different than that for water.

The above experimental fact allowed to establish a concept of specific heat capacity for each material as an amount of heat required to increase the temperature of a unit of mass of this material (1 kg in SI) by a unit of temperature (1°C or 1°K in SI).

Thus, specific heat capacity of water is, as we know, one kilocalorie per kilogram per degree - 1 kcal/(kg·°K), that is about 4184 joules per kilogram per degree - 4183 J/(kg·°K).
For copper the specific heat capacity is 385 J/(kg·°K).
Gold has the specific heat capacity of 129 J/(kg·°K).
Uranium's specific heat capacity is 116 J/(kg·°K).
Cotton's specific heat capacity is 1400 J/(kg·°K).
Hydrogen's specific heat capacity is 14304 J/(kg·°K).
Generally speaking, but not always, more dense, more solid materials have less specific heat capacity than less dense or liquids, which have, in turn, less specific heat capacity than gases.

Knowing specific heat capacityC of material of an object and its mass m, we can easily determine amount of energy ΔQneeded to heat it up by ΔTdegrees:
ΔQ = C·m·ΔT
Inversely, knowing the amount of heat supplied, we can determine an increase in temperature:
ΔT = ΔQ/(C·m)
Notice, that increment of temperature ΔT and increment of heat energy ΔQ can be both positive or both negative, which means that an object, that has increased its temperature, has increased (gained, consumed) energy, and the object that decreased its temperature, has decreased (lost, released) energy.

Change of State

Consider specific heat capacity of ice and water:
Ice: 2090 J/(kg·°K)
Water: 4183 J/(kg·°K)
Both these substances exist at temperature about 0°C=273°K. That means that we can heat 1 kg of ice up to 0°C spending 2090 joules per each degree of temperature, but to increase the temperaature of the water around 0°C we have to spend 4183 joules per each degree. But, while ice is melting into water, which takes some time, both states, solid and liquid, exist side by side and the temperature of the water will not rise while the ice is not completely melted, we have to spend heat energy just on melting without actually changing the temperature of a substance, that remains around 0°C during the melting process.

This experimental observation leads us to believe that, while graduate change of temperature for any specific state of matter linearly depends on the amount of heat supplied, change of state (like melting or freezing, or evaporating etc.) brings an element of non-linearity to this dependency.
More precisely, the temperature, as a function of amount of heat supply, in case of an object going through transformation of state from solid to liquid, looks like this (for better view, right click on the picture and open it in another tab of a browser):

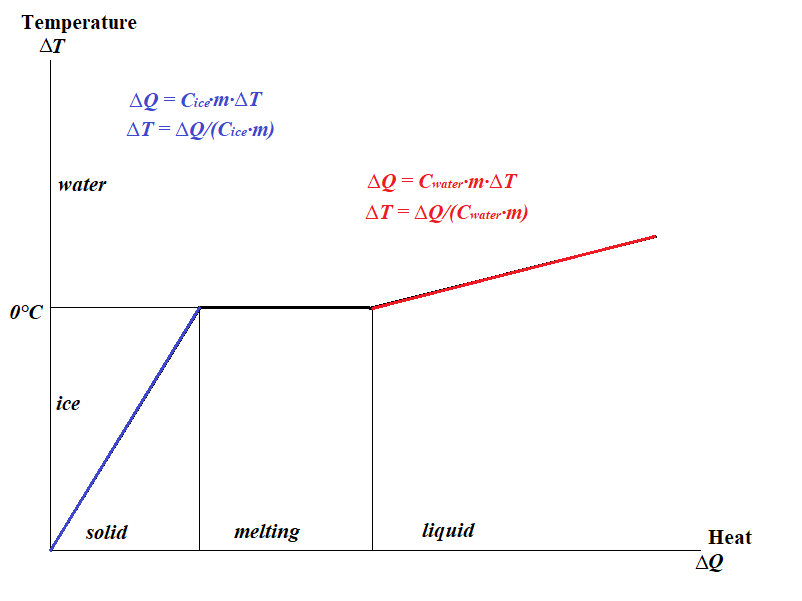
As seen on this graph, supplying heat to ice will increase its temperature proportionally to amount of heat supplied.
Then, when the temperature reaches 0°C, ice will start melting and new heat will not change the temperature of ice/water mix, but will be used to change the state of matter from solid (ice) to liquid (water).

This process of melting consumes heat without increasing the temperature until all ice is melted. Such a transformation of state that requires supply of heat energy is called endothermic.
Then, when the process of melting is complete, and all ice is transformed into water, the temperature of water will start increasing, as the new heat is supplied, but with a different coefficient of linearity relatively to the heat than in case of ice, since water's specific heat capacity is different than that of ice.
The graph above is characteristic to any heating process, where the transformation of the state of matter is involved. It is relatively the same for transforming liquid to gas (evaporation) or solid to gas (sublimation).

In case of a reversed transformation from liquid to solid (freezing) or gas to liquid (condensation) or gas to solid (deposition) the heat energy must be taken away from a substance. It is the same amount in absolute value as was needed to supply to solid to melt it into liquid or to liquid to vaporise it into gas, or to solid to vaporize it into gas. So, in case of freezing, condensation or deposition we deal with the process of decreasing heat energy of a substance. Such a process is called exothermic.

Amount of heat energy needed to transform a substance from one state to another is also experimentally determined and, obviously, depends on a substance, its mass and a kind of transformation it undergoes.
For example, melting of 1 kg of ice requires 333,000 joules of heat energy to be supplied. The same amount of heat energy should be extracted from the water at 0°C to freeze it into ice.

Unizor - Physics4Teens - Energy - Heat - Measuring

Notes to a video lecture on http://www.unizor.com

Measuring Heat - Calorie

Heat and temperature were known and researched by scientists long before the molecular movement was determined as their essence. As a result, attempts of measuring the amount of heat were unrelated to kinetic energy of the molecules.

The unit of amount of heat was defined as amount of heat needed to increase the temperature of one gram of water by one degree Celsius (or Kelvin), and this unit of amount of heat was called a calorie (cal).

Obviously, this definition has its flaws. For example, the amount of heat needed to heat the same amount of water by the same temperature depends where exactly on Earth we are. The higher we are above the sea level - the less heat is needed. It also depends on the chemical purity of water. Also it's not obvious that the amount of heat needed to heat the water from 1°C to 2°C is the same as amount of heat needed to heat it from 88°C to 89°C, though within reasonable level of precision we do assume that this is true.

With the development of molecular theory of heat and establishing relationship between heat and kinetic energy of molecules there was a need to put into correspondence existing units of heat (calories) and units of mechanical energy (joules). A simple experiment allowed to do just that.

Imagine a standing on the ground large reservoir with known amount of water M of depth H from the surface to the bottom, kept at certain known temperature T°, and a relatively small stone of known mass m, having the same temperature T°, kept on the level of the surface of the water in a reservoir. This stone has certain known amount of potential energy E=m·g·Hrelatively to the bottom level of a reservoir.
Now we let the stone go down the reservoir to its bottom. Its potential energy relatively to the bottom of a reservoir decreases to zero. Where did the potential energy go? It's used to stir the water, thereby increasing the kinetic energy of its molecules.

Because of this more intense movement of molecules, the water will increase its temperature. Potential energy of a stone will turn into kinetic energy of the molecular movement of water. If the temperature of the water has risen by ΔT°, potential energy of a stone m·g·H (in joules) equals to M·ΔT (in calories).

Precise experiments like the above allowed to determine the correspondence between historical measure of the amount of heat in calories under different conditions and contemporary one in units of energy in SI - joules. This correspondence had been established approximately as
1 calorie = 4.184 joules
but under different conditions (initial temperature, air pressure etc.) it might be equal to a slightly different value.

Besides calorie, which is a relatively small amount of heat, the unit kilocalorie (kcal) had been introduced.
As is obvious from its name, 1 kilocalorie = 1000 calories.

The amount of energy contained in food and in some other practical cases very often is measured in kilocalories, which sometimes are called large calories, while a calorie is sometimes called small calorie. Unfortunately, the word "large" in many cases is omitted, which might cause misunderstanding.
From the experimental viewpoint, 1 kcal is amount of heat needed to heat 1 kg of water by one degree Celsius (or Kelvin).

To avoid problems with the definition of calorie as amount of heat needed to warm up one gram of water by one degree Celsius, the contemporary scientific definition of thermocalorie is
1 thermocalorie = 4.1833 joules

Unizor - Physics4Teens - Energy - Ideal Gas Kinetics - Problems

Notes to a video lecture on http://www.unizor.com

Problem 1

How much kinetic energy have all the molecules in the room?
How fast should an average size car move to have this amount of kinetic energy?

Assume the following:
(a) the room dimensions are 4x4x3 meters (that is, V=48m³);
(b) normal atmospheric pressure is 100,000 Pascals (that is, p=100,000N/m²);
(c) a mass of an average size car is 2,000 kg (that is, M=2,000kg).

Solution

From the lecture on Kinetics of Ideal Gas we know the relationship between the pressure on the walls of a reservoir, volume of a reservoir and total kinetic energy of gas inside this reservoir:
p = (2/3)E_tot /V

From this we derive a formula for total kinetic energy:
E_tot = (3/2)·p·V

Substituting the values for pressure and volume, we obtain
E_tot = (3/2)·100,000·48 =
= 7,200,000(joules)

The kinetic energy of a car is
E = M·v²/2
Therefore, given the kinetic energy and mass, we can determine the car's speed:
v = √2·E/M
Substituting calculated above E_tot=7,200,000(J) for E and the value for mass M=2,000(kg), we obtain
v = √2·7,200,000/2,000 ≅
≅ 85(m/sec) ≅
≅ 306(km/hour) ≅
≅ 190(miles/hour)


Problem 2

Given the temperature, pressure and volume of the air in a room, determine the number of gas molecules in it.

Assume the following:
(a) the room dimensions are 4x4x3 meters (that is, V=48m³);
(b) normal atmospheric pressure is 100,000 Pascals (that is, p=100,000=10⁵N/m²);
(c) temperature is 20°C (that is, T=20+273=293°K).

Solution
Recall the combined law of ideal gas
p·V/T = k_B·N = const
where
k_B = 1.381·10⁻²³ (J/°K) is Boltzmann's constant and
N is the number of gas molecules in a reservoir.
From this we derive the number of molecules
N = p·V/(k_B·T)
Substituting the values,
N = 10⁵·48/(1.381·10⁻²³·293) = 0.12·10²⁸
It's a lot!