Unizor - Physics4Teens - Mechanics - Statics - Equilibrium of Solids

Notes to a video lecture on http://www.unizor.com



Equilibrium of Solids



As we know, if a vector sum of forces, acting on a point-object, equals
to null-vector, this point-object is at rest or in a state of uniform
motion along a straight line in any inertial frame of reference.
Alternatively, we can say that a frame of reference associated with this
point-object is inertial.



The complexity of a concept of equilibrium of solids lies in the fact
that, even if vector sum of forces, acting on a solid, equals to
null-vector, this solid might not be in the state of rest in any
inertial system. In a simple case of two forces, equal in magnitude and
opposite in direction, applied to two different points of a solid, will
rotate it, making a frame of reference associated with it non-inertial.





Any rotation of a solid, however complex, can be represented as a
combination of three rotations around three coordinate axes. Therefore, a
solid in a state of equilibrium should be in equilibrium relative to
each coordinate axis, and, to study equilibrium of a solid in
three-dimensional space, it is sufficient to study it relative to one
axis.



As we know, in case of rotation around an axis, the main factor replacing a concept of force for translational movement, is torque. Since torque is a cause of rotation, the necessary condition to prevent a rotation is balancing of torques.



Torque is a vector equal to a vector (cross) product of a radius-vector r from the axis of rotation to a point of application of force (perpendicularly to the axis) by a vector of force:

τ = r×F 



Using this concept of torque, we can formulate the following necessary condition for an equilibrium of a solid.

Sum of torques of all forces acting on a solid relative to each coordinate axis must be equal to null-vector.



In the previous lecture we introduced a concept of a degree of freedom
and, in particular, mentioned six degrees of freedom of a solid: three
degrees of freedom along each coordinate axis and three degrees of
freedom of rotation around each coordinate axis.



If a vector sum of all forces acting on a solid is a null-vector, there
will be a point that is not moving anywhere or, more precisely, a frame
reference associated with this point is inertial. This condition assures
an equilibrium by three degrees of freedom associated with
translational motion (a motion along coordinate axes).



If a vector sum of all torques relatively to each of the three
coordinate axes is a null-vector, there will be no rotation and the
system will be in equilibrium by three other degrees of freedom
associated with rotational motion (a motion around coordinate axes).



So, for a solid to be in equilibrium, the necessary conditions are
all of the above - sum of all the forces and sum of all the torques must
be null-vectors.



Consider the following example.

A weightless rod of a length 2r is hanging horizontally on a thread fixed at its midpoint.

On both ends of a rod there are equal weights W hanging down.



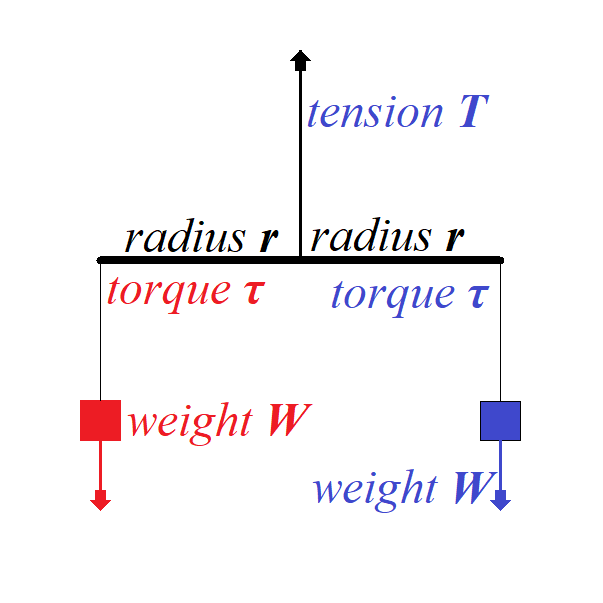
To balance the translational movement of a system vertically down the force of tension T on a thread that holds the rod must balance a sum of forces of weight acting in opposite direction:

T  + W  + W  = 0 

T  = −2W 



To balance the rotational movement of a system around a midpoint of a
rod the torque of one weight should be equal in magnitude to the torque
of another weight since the directions of these two torques are
opposite:

τ _blue = r ×W 

τ _red = −r ×W 

τ _red + τ _blue = 0 



Consider a less symmetrical case below.

Here a rod of the length 3r is hanging by a thread fixed not in the middle, but at a distance r from the left edge and, therefore, at a distance 2r from the right edge.

At the same time, the weight on the left is twice as heavy as the one on the right.



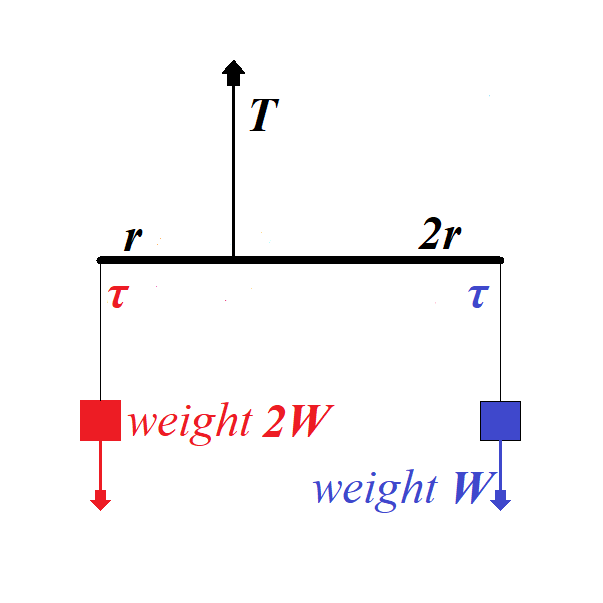
Tension on the thread holding a rod must be greater to hold more weight:

T  + W  + 2W  = 0 

T  = −3W 



From the rotational viewpoint, this system is in equilibrium because the
torques on the left of a rod and on the right are equal in magnitude,
while opposite in direction:

τ _blue = 2r ×W 

τ _red = −r ×2W 

τ _red + τ _blue = 0

Unizor - Physics4Teens - Mechanics - Statics - Point-Objects

Notes to a video lecture on http://www.unizor.com



Equilibrium of Point-Objects



The state of equilibrium in a case of possibility of a
point-object to move in some direction implies that the position of this
object does not change, which, in turn, implies that the vector sum of
all forces acting on it is a null-vector:

ΣF_i = 0 .



In three-dimensional world each force F_i
has three components - the projections of this force on X-, Y- and
Z-axis. In order for a sum of vectors to be equal to a null-vector, it
is necessary and sufficient for a sum of their X-components to be equal
to 0, same for Y- and Z-components.

Therefore, we can construct three equations, one for each axis, to determine forces participating in the state of equilibrium:

ΣF_i^(x) = 0

ΣF_i^(y) = 0

ΣF_i^(z) = 0



The fact that only three equations determine the conditions on forces to
be in equilibrium in a three-dimensional world means that unique
determination of these forces is possible only if the number of unknowns
does not exceed three. If four or more unknown variables participate in
the state of equilibrium, we will have infinite number of solution of
the system of three linear equations with four or more unknowns.

Most likely, for our purposes we will consider situations with only unique solutions.



As a simple example of an equilibrium in three-dimensional space,
consider a chandelier of some weight hanging from a ceiling on three
threads attached to a ceiling at three different points. For simplicity,
assume that a chandelier is a point-object and three points of
attachment of the threads to a ceiling are making an equilateral
triangle and the length of all threads is the same.



The weight of a chandelier W is balanced by three equal in magnitude T,
but acting at different angles, tension forces along each thread.
Knowing the weight of a chandelier and an angle of each thread with a
vertical φ (the same for each thread in our simple case), we can easily determine the magnitude of the tension force of each thread:

3·T·cos(φ) = W

T = W / [3·cos(φ)]

Here we only constructed the equation along the vertical Z-axis because
in a horizontal plane (along X- and Y-axis) the tension forces balance
each other.



The example above is a perfect illustration to our next discussion.



Stable Equilibrium



We call an equilibrium stable if, after a small movement of an object from its position of equilibrium, it returns back to this position.



A small push of a chandelier will result in its light swinging and eventual return to the original position of equilibrium.



Consider a cup in a form of semi-sphere and a small ball at the bottom of this cup. It lies in the state of stable equilibrium. If we push it off this position, it will eventually return back because the sum F of reaction force R of the cup and the weight W of a ball always act in a direction of the lowest point of this semi-spherical cup.



Let's formulate the definition of a stable equilibrium in more precise terms.

For this we have to consider a position of an object in equilibrium and
its immediate neighborhood. Since we consider the equilibrium to be
stable, we have to consider the deviation of an object from a position
of equilibrium.

Basically, we would like to say that the equilibrium is stable, if an
object returns to it from any neighboring point. How big is the
neighborhood, from which this return takes place is, obviously, a
subject of a definition.

The rigorous definition of a stable equilibrium defines the neighborhood as any, however small, one.



So, if exists a real positive value ε such that from any point within ε-neighborhood
of a position of equilibrium an object, placed at this point, returns
to a position of equilibrium, the equilibrium is stable.



Unstable Equilibrium



The unstable equilibrium is the opposite of a stable one. That
means that any, however small, deviation of the object's position from
the position of equilibrium results in moving of this object away from
the equilibrium point.

Obvious example is a small ball on the top of a sphere. If its position
is exactly at the North Pole, it's in equilibrium. But any, however
small, deviation from the NorthPole results in complete departure from
the position of equilibrium.



Neutral Equilibrium



Consider a ball on a horizontal plane. There are two forces acting on it
- gravity vertically down and reaction of the plane vertically up and
equal in magnitude to the ball's weight. These two forces neutralize
each other, no matter where on the plane our ball is positioned. So, any
position is a position of equilibrium. This is exactly what neutral equilibrium is.

Any deviation from the position of neutral equilibrium results in the new equilibrium.

Strictly speaking, neutral equilibrium implies existence of some
neighborhood around the position of equilibrium such as any position
within this neighborhood is a position of equilibrium.



Solids and Six Degrees of Freedom



Before we talked about equilibrium of a point-object, that is a state of
rest, when all forces applied to it are in balance and their sum is
null-vector.

Let's expand our concept of equilibrium to solids. Obviously, they not
only can move in three different directions (forward-backward along
X-axis, left-right along Y-axis, up-down along Z-axis), but also can
rotate around any of the three coordinate axis.

That means that a position of a solid is determined by six parameters - so called six degrees of freedom. Equilibrium of this solid object implies its state of rest along each of these six degrees of freedom.



We know how to deal with the first three degrees of freedom associated with translational motion.

Conditions of equilibrium related to rotation - the other three degrees of freedom - will be analyzed in the next section.

Unizor - Physics4Teens - Mechanics - Rotational Dynamics - Conservation ...

Notes to a video lecture on http://www.unizor.com



Conservation of
Angular Momentum



We ended up the previous lecture deriving the Law of Conservation of
Angular Momentum. In this lecture we will continue discussing this
particular conservation law.

We will consider a thought experiment suggested by Arkady Kokish in our private discussion of this topic.

The results of this thought experiment will confirm the Angular Momentum Conservation Law.



Consider a point-object of mass M with no external forces (like gravity) present and two threads, short of length r and long of length R tied to it.

A person holds both threads and starts spinning an object with angular velocity ω₁. It will rotate along a circular trajectory of a radius r (the length of a shorter thread).

Let's analyze what happens if this person lets a shorter thread go, while holding the long one.



On the picture above the short thread is let go when an object was at
the top. Then, since nothing holds it on a circular trajectory, it will
fly along a tangential line maintaining the same linear speed it had
when it was rotating, that is r·ω₁.



But our object will not fly too far. The longer thread will stop it, when it will be on a distance R from a center of rotation.

Here is a picture of this particular moment, when the long thread is fully extended.



At this moment the linear speed of an object flying (on the picture) left to right equals to V=r·ω₁.

Let's represent this vector as a sum of two vectors: V_t perpendicular to a line representing the fully extended long thread (tangential to a future circular trajectory of a radius R) and V_r going along that thread line (radial).



Assuming an angle between a short thread at a moment it was let go and a
long one at the moment it is fully extended, stopping tangential
movement of an object, is φ, it is obvious that r=R·cos(φ).



At the moment when the long thread is fully extended the tension of the
thread instantly (actually, during a very short interval of time Δt) nullifies the radial speed V_r. To be exact, its moment of inertia M·V_r will be equal to an impulse of the tension force T during interval of time Δt:

T·Δt = M·V_r

This tension force decelerates the radial speed to zero during the interval of time Δt. The shorter this interval - the more ideal our experiment is.

In an ideal case of non-stretchable thread that can withstand infinite tension the interval Δt is infinitely small, and deceleration is infinitely large in magnitude and short in time.

In this case the radial speed V_r will be brought down to zero instantaneously.



At the same time the magnitude of tangential vector of speed V_t is not affected by the tension since this vector is perpendicular to a tension force.



We see that the angle between vectors V=r·ω₁ and V_t is the same as between threads φ.



Therefore, V_t = r·ω₁·cos(φ)

But cos(φ) = r/R

from which follows

V_t = r·ω₁·r/R

Tangential linear speed V_t is related to angular speed of rotation ω₂ of our object on a new radius R as V_t=R·ω₂.

Hence,

R·ω₂ = r·ω₁·r/R

R²·ω₂ = r²·ω₁

M·R²·ω₂ = M·r²·ω₁

Expression M·r² represents the moment of inertia I₁ of an object of mass M rotating on a radius r.

Analogously, expression M·R² represents the moment of inertia I₂ of the same object of mass M rotating on a radius R.



Therefore, we have derived the Law of Conservation of the Angular Momentum:

I₁·ω₁ = I₂·ω₂