Notes to a video lecture on http://www.unizor.com
Conservation of
Angular Momentum
We ended up the previous lecture deriving the Law of Conservation of
Angular Momentum. In this lecture we will continue discussing this
particular conservation law.
We will consider a thought experiment suggested by Arkady Kokish in our private discussion of this topic.
The results of this thought experiment will confirm the Angular Momentum Conservation Law.
Consider a point-object of mass M with no external forces (like gravity) present and two threads, short of length r and long of length R tied to it.
A person holds both threads and starts spinning an object with angular velocity ω1. It will rotate along a circular trajectory of a radius r (the length of a shorter thread).
Let's analyze what happens if this person lets a shorter thread go, while holding the long one.

On the picture above the short thread is let go when an object was at
the top. Then, since nothing holds it on a circular trajectory, it will
fly along a tangential line maintaining the same linear speed it had
when it was rotating, that is r·ω1.
But our object will not fly too far. The longer thread will stop it, when it will be on a distance R from a center of rotation.
Here is a picture of this particular moment, when the long thread is fully extended.
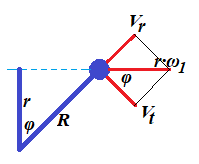
At this moment the linear speed of an object flying (on the picture) left to right equals to V=r·ω1.
Let's represent this vector as a sum of two vectors: Vt perpendicular to a line representing the fully extended long thread (tangential to a future circular trajectory of a radius R) and Vr going along that thread line (radial).
Assuming an angle between a short thread at a moment it was let go and a
long one at the moment it is fully extended, stopping tangential
movement of an object, is φ, it is obvious that r=R·cos(φ).
At the moment when the long thread is fully extended the tension of the
thread instantly (actually, during a very short interval of time Δt) nullifies the radial speed Vr. To be exact, its moment of inertia M·Vr will be equal to an impulse of the tension force T during interval of time Δt:
T·Δt = M·Vr
This tension force decelerates the radial speed to zero during the interval of time Δt. The shorter this interval - the more ideal our experiment is.
In an ideal case of non-stretchable thread that can withstand infinite tension the interval Δt is infinitely small, and deceleration is infinitely large in magnitude and short in time.
In this case the radial speed Vr will be brought down to zero instantaneously.
At the same time the magnitude of tangential vector of speed Vt is not affected by the tension since this vector is perpendicular to a tension force.
We see that the angle between vectors V=r·ω1 and Vt is the same as between threads φ.
Therefore, Vt = r·ω1·cos(φ)
But cos(φ) = r/R
from which follows
Vt = r·ω1·r/R
Tangential linear speed Vt is related to angular speed of rotation ω2 of our object on a new radius R as Vt=R·ω2.
Hence,
R·ω2 = r·ω1·r/R
R²·ω2 = r²·ω1
M·R²·ω2 = M·r²·ω1
Expression M·r² represents the moment of inertia I1 of an object of mass M rotating on a radius r.
Analogously, expression M·R² represents the moment of inertia I2 of the same object of mass M rotating on a radius R.
Therefore, we have derived the Law of Conservation of the Angular Momentum:
I1·ω1 = I2·ω2


No comments:
Post a Comment