Notes to a video lecture on http://www.unizor.com
Problems on
Rotational Dynamics
Problem 1
Consider a device that consists of a wheel of radius r and mass M, freely rotating on some fixed axis, a thread rolled around it a few times and a point-object of mass m hanging off that thread.
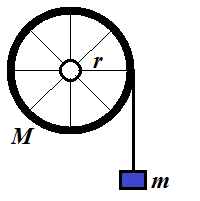
Assume that all mass of a wheel is concentrated in its rim, while spokes are weightless.
There is no friction in the rotating wheel.
A thread is weightless and unstrechable.
The force of gravity pulls the object down with free fall acceleration g.
What will be the acceleration of an object?
Solution
The weight of a wheel is balanced by the reaction of fixed axis and, therefore, can be ignored.
The only force acting tangentially on a wheel is the tension of a tread T trying to rotate it.
Therefore, we can equate its momentum τ=T·r (torque) to a product of its moment of inertia I and angular acceleration α:
τ = T·r = I·α
The fact that all mass of a wheel is concentrated in its rim allows us
to easily calculate its moment of inertia. We can imagine a rim
consisting of a large number N of point-objects of mass M/N each. The moment of inertia of each is (M/N)·r² and combined moment of inertia of a wheel is N·(M/N)·r²=M·r². If the mass is not concentrated in the rim, analogous logic would lead us to more involved calculations of inertial mass.
Considering, I=M·r² and r·α=a (where a is a linear acceleration of a thread) we can write the following equation:
T·r = M·r²·a/r = M·r·a
Radius cancels out and we get
T = M·a
Notice that this is exactly the same equation as the Newton's Second Law, as if an object of mass M is pulled along a straight line by a force T with linear acceleration a.
Another important detail is that this formula is independent of a radius
of a wheel - a direct consequence of the fact that the mass of a wheel
is concentrated in its rim.
Analyzing the movement of an object hanging on a thread, we conclude that it moves with linear acceleration a down by the forces of gravity (directed down) and tension of a thread (directed up). Therefore, using the Newton's Second Law,
m·g − T = m·a
Now we have a system of two equations with two unknowns T and a, which is easy to solve.
Substitute T from the first equation to the second:
m·g − M·a = m·a
m·g = (M + m) · a
a = m·g / (M + m)
Problem 2
Calculate a moment of inertia of disk of mass M and radius R rotating around an axis going through its center perpendicularly to its surface.
Solution
Divide a disk into a set of concentric rings of infinitesimal width dr. Let the inner radius of a particular ring be r and it outer radius be r+dr.
Moment of inertia of each ring is
I(r) = m·r²
where m is its mass (see the previous Problem 1 for explanation).
Mass of a ring m is a mass of a disk M multiplied by a ratio of a ring's area 2πr·dr to the area of an entire disk πR².
So, the moment of inertia of our ring of radius r and infinitesimal width dr is
I(r) = [M·2πr·dr/(πR²)]·r²
Integrating this from r=0 to r=R, we get
Idisk(M, R) =
= ∫[M·2πr·dr/(πR2)]·r2 =
= (2M/R2)∫r3dr =
= (2M/R2)·(r4/4) =
= M·R2/2
Problem 3
Consider Problem 1, but change a wheel with all mass concentrated in the
rim with a wheel with mass evenly distributed inside the circumference,
making it a disk.
Solution
We follow the same logic as in Problem 1.
The weight of a wheel is balanced by the reaction of fixed axis and, therefore, can be ignored.
The only force acting tangentially on a wheel is the tension of a tread T trying to rotate it.
Therefore, we can equate its momentum τ=T·r (torque) to a product of its moment of inertia I and angular acceleration α:
τ = T·r = I·α
The fact that all mass of a wheel is evenly distributed within its
circumference allows us to easily calculate its moment of inertia using
the Problem 2 above:
I=M·r²/2
Linear acceleration a and angular acceleration α are related:
r·α=a
Therefore,
T·r = [M·r²/2]·(a/r) = M·r·a/2
Radius cancels out and we get
T = M·a/2
An important detail is that this formula is independent of a radius of a wheel.
Analyzing the movement of an object hanging on a thread, we conclude that it moves with linear acceleration a down by the forces of gravity (directed down) and tension of a thread (directed up). Therefore, using the Newton's Second Law,
m·g − T = m·a
Now we have a system of two equations with two unknowns T and a, which is easy to solve.
Substitute T from the first equation to the second:
m·g − M·a/2 = m·a
m·g = (m + M/2) · a
a = m·g / (m + M/2)
If we compare this formula with the one in Problem 1, we see that final acceleration is greater because denominator is smaller.
So, the disk in this problem will rotate faster than a wheel with empty middle part from Problem 1.
Problem 4
Let's rotate a small ball of mass M within a horizontal plane on a thread of length D. The thread will make certain angle φ with the horizon. Experiments show that the angle will be smaller if a ball rotates faster.
Determine the relationship between angular speed of rotation ω, mass of a ball M, length of a thread D and angle φ, ignoring friction and air resistance.
Solution
The tension of a thread T keeps a ball on its orbit. Radius of an orbit is R=D·cos(φ).
The tension of a thread T serves dual purpose - its vertical component T·sin(φ) acts against gravity M·g, its horizontal component T·cos(φ) acts as a centripetal force and should be equal to M·V2/R, where V is a linear speed of a ball, which is equal, in turn, to R·ω, where ω is angular speed of rotation of a ball.
So, we have the following equations:
T·sin(φ) = M·g
T·cos(φ) = M·(V2)/R = M·R·ω2 = M·D·cos(φ)·ω2
The second equation is simplified to
T = M·D·ω2
Substituting it to the first equation,
D·ω2·sin(φ) = g
Therefore,
sin(φ) = g/[D·ω2]
For a given angular speed we can find an angle of a thread to horizon φ. It in inversely proportional to a length of a thread D and to a square of angular speed ω, which seems to be reasonable.
Interestingly, this angle is independent of the mass M.


No comments:
Post a Comment