Unizor - Physics4Teens - Mechanics - Statics - Equilibrium

Notes to a video lecture on http://www.unizor.com



Equilibrium



Statics is a part of Mechanics that studies forces not as
quantitative measure of a motion they cause (that is a subject of
Dynamics), but from the more fundamental viewpoint of whether these
forces are or are not balanced, that might or might not cause the motion
of objects these forces act upon.



Historically, studies of static aspects of forces precede quantitative
studies of motion in Dynamics. People, first of all, were concerned with
how to build bridges and buildings, so that they stay in place and not
destroyed by gravity, wind or load. And a concept of equilibrium is a central point of Statics, it's goal and purpose.



Equilibrium, as it is understood in Statics, is a state of forces, that result in an object acted upon to be in the state of rest.



A person standing on a floor is at rest because two main forces that act
upon him, the gravity and the reaction of the floor are equal in
magnitude and opposite in direction, they balance each other, which
results in a state of equilibrium.



A person standing on the weights to check his weight is in a state of equilibrium
because its weight is balanced by elastic force inside the weights that
is equal in magnitude and opposite in direction to the force of
gravity. The equality in magnitude allows to measure the weight by
measuring the elasticity inside the weights.



A building is in a state of equilibrium because its each part's weight is balanced by equal in magnitude and opposite in direction force of reaction.



An airplane, flying horizontally on its route, is in a state of vertical equilibrium
because its weight is balanced by the lifting power of the air under
its wings, where the air pressure is larger because of the wings' shape.



Let's study forces applied to the same object and balance each other causing this object to be in equilibrium.

As we know, force is a vector. All forces acting on the same point-object can be added as vectors, using the rules of the Vector Algebra.

If the result is a null-vector, we have an equilibrium.



So, if there are N forces F_i (where 1 ≤ i ≤ N) acting simultaneously on the same point-object, the condition of equilibrium is

ΣF_i = 0 .



Let's consider a few examples.



1. An object of weight W is hanging on three threads as pictured below.



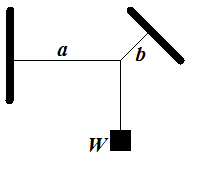
Thread a is horizontal, thread b is at angle φ to horizon.

The system is in equilibrium.

What is the magnitude of tension forces T_a and T_b on threads a and b?



Solution

There are three forces acting at the point where all threads are connected:

vertical down - the weight W of the object;

tension T_a horizontally to the left along the a thread;

tension T_b at angle φ to horizon along the b thread.

Since the system is in equilibrium, this point where threads come
together does not move in any direction. In particular, it does not move
in a vertical, nor horizontal direction.

This is sufficient to determine magnitude of tension vectors T_a and T_b.

In the horizontal direction the force of gravity is irrelevant, so the
only two forces acting on out object in horizontal direction are tension
T_a acting to the left and a projection of tension T_b on the horizontal line acting to the right.

That gives the first equation about magnitudes of tension forces:

T_a = T_b·cos(φ)

Now consider the vertical direction. The thread a is irrelevant. So, the only two forces acting vertically, are weight W pulling down and a vertical component of T_b that is equal to T_b·sin(φ) pulling upwards.

This gives the second equation

T_b·sin(φ) = W

From these equations we derive:
T_b = W/sin(φ)

After which we can find T_a:

T_a = W·cos(φ)/sin(φ)



2. Two objects of mass M (larger, on an inclined plane) and m (smaller, hanging freely over the edge of an inclined plane) are connected with a thread that goes over a pulley.



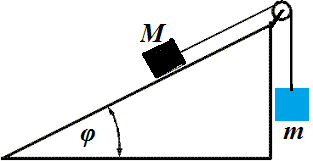
What is the angle of an inclined plane φ for this system to be in equilibrium?

Ignore the friction.



Solution

Let's represent the weight of an object on an inclined plane as a sum of two forces:

one is perpendicular to the plane and balanced by a plane's reaction;

another is parallel to the plane and balanced by a tension of a thread.

To be in equilibrium, the force of weight of an object hanging freely
over the edge of an inclined plane must be equal in magnitude to a
tension of a thread (same thread, same tension as before).

Therefore, a component of the weight of an object on a plane that goes
parallel to a plane must be equal in magnitude to a weight of another
object.

M·g·sin(φ) = m·g

From this we derive

sin(φ) = m/M

φ = arcsin(m/M)