Unizor - Double Integrals - Volume of Pyramid

Notes to a video lecture on http://www.unizor.com

Double Integrals - Pyramid

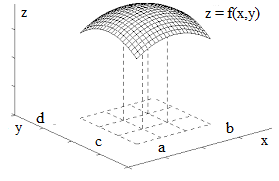
As another example of a double integral as a volume of a solid, consider a pyramid with three plains coinciding with three coordinate planes as follows:
base is a right triangle with vertex of the right angle at the origin of coordinates O and catheti OA (along the X-axis) and OB (along the Y-axis);
point C on the Z-axis is the top vertex of this pyramid.

Let the lengths of these sides be
OA = a
OB = b
OC = c
Our task is to calculate the volume of this pyramid using the double integral and techniques described in the previous lecture.



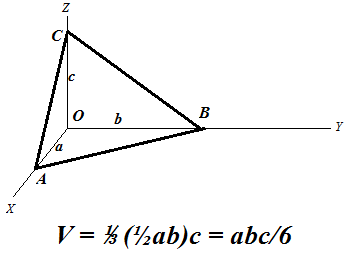
We can consider this problem as the problem of determining a volume of a solid bounded on the top by a plane going through three given points A, B and C and defined on the base triangle ΔOAB lying in the XY-plane.

Since we intend to integrate a function to determine a volume, let's express the plane going through points A, B and C as a function f(x,y) of two arguments x and y - coordinates of a point that belong to a base triangle.
Traditional equation of this plane in three-dimensional coordinates is
x/a + y/b + z/c = 1
from which follows the functional representation
z = f(x, y) = c·(1 − x/a − y/b)

Since our base in not rectangular, we have to pick the primary argument, let it be x changing from 0 to a. The argument y has limits that depend on the value of x in order for point (x, y) to be within our triangle. For each x, therefore, argument y should change from 0 to a point on the hypotenuse of our base triangle.
Equation of this line on a plane that goes through points A on the X-axis and B on the Y-axis is
x/a + y/b = 1
Therefore, the point on a hypotenuse that corresponds to X-coordinate x is
y = b·(1 − x/a)



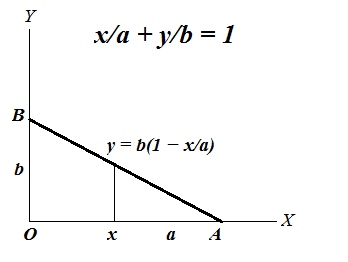
So, for each primary coordinate x (from 0 to a) coordinate y is changing from 0 to b·(1 − x/a).

Using exactly the same logic as in the previous lecture, we can express the volume of this pyramid as a double integral of function
f(x, y) = c·(1 − x/a − y/b)
on a base triangle ΔOAB described by primary argument x changing from 0 to a and dependent argument y changing from 0 to b·(1 − x/a).

Now the formula for a volume of our pyramid would be
V = ∫₀^a [∫₀^b·(1−x/a) f(x,y) dy] dx
where
f(x, y) = c·(1 − x/a − y/b)

Let's perform the inner integration by y considering x constant.
∫₀^b·(1−x/a) f(x,y) dy =
= ∫₀^b·(1−x/a)c·(1−x/a−y/b) dy =
= c·(1−x/a) ∫₀^b·(1−x/a) dy − (c/b) ∫₀^b·(1−x/a)y dy =
= b·c·(1−x/a)²−b·c·(1−x/a)²/2 =
= b·c·(1−x/a)²/2
Now, to get the volume of our pyramid, we have to integrate this as a function of x from 0 to a:
V = ∫₀^a b·c·(1−x/a)²/2 dx
In this case, to integrate it, let's make a substitution
t = 1−x/a
Then we can express x, its differential dx and limits of integration 0 and a in terms of t:
x = a − a·t
dx = −a·dt
x=0 ⇒ t=1
x=a ⇒ t=0

As a result of this substitution,
V = ∫₁⁰ b·c·t²/2 (−a)·dt =
= (a·b·c/2)·∫₀¹t²dt =
= (a·b·c/2)·(1/3) = a·b·c/6
which corresponds to a known formula for a volume of a pyramid.

Unizor - Double Integrals - Circular Base

Notes to a video lecture on http://www.unizor.com

Double Integrals -
Circular Base

Previous lecture introduced a concept of a double integral as a volume of a solid with a rectangular base.
In particular, we came to a conclusion that in this case we can integrate, first, by one of the argument and then by another or, equally well, in an opposite order. Rectangular base of a solid allowed such a freedom.

In this lecture we will consider a solid with a circular base and, which is important, the technique of calculating the volume of this solid would be valid for many other types of bases, not necessarily circular. Another important point is that the integration in one order cannot be performed in another order without modifications.

Consider the following problem.
Given a smooth function of two variables f(x, y) with non-negative values (that is, f(x, y) ≥ 0), defined on an area bounded by a circle of a radius R with a center at the origin of coordinates, and represented by a surface in (X,Y,Z) coordinate space.



Our task is to find the "volume of a solid" - the measure of a part of coordinate space bounded on the top by a surface representing this function, on the bottom - by X,Y-plane and sides forming a cylindrical surface based on a circle described above, rising on a height determined by the values of our function on the circle's border.

We will follow the same logic as in a case of a rectangular base.
The process of approximation starts with dividing our circular base into many small rectangles by lines x=x_i (where i∈[0,M], x₀=−R, x_M=R) and y=y_j (where j∈[0,N], y₀=−R, y_N=R) and constructing rectangular parallelepipeds on the base of these small rectangles with the height equaled to a value of function f(x, y) in the corner of each base rectangle with largest coordinates x and y ("top right corner").

If point (x_i, y_j) represents the coordinates of a "top right" corner of a small base rectangle and Δx_i=x_i−x_i−1, Δy_j=y_j−y_j−1are sides of this small rectangle, the volume of a constructed rectangular parallelepiped equals to
ΔV_i,j = f(x_i, y_j)·Δx_i·Δy_j

The combined volume of all these parallelepipeds approximates the volume of our solid. With increasing number of small base rectangles and, correspondingly, decreasing their dimensions we assume that there is a limit of the combined volume of all these parallelepipeds.
It can be proven that under certain conditions of smoothness of our function f(x, y) the limit does exist and is unique, regardless of the way how exactly we divide the domain of our function into small rectangles, as long as their dimensions are converging to zero (or, more precisely, the dimensions of the largest among them converges to zero).

Now let's consider how we can summarize the volumes of all parallelepipeds constructed on the basis of small rectangles. We cannot summarize all x_i and y_j, as we did in a case of a rectangular base, because many of them will go outside of a circle where the function is undefined.
Instead, let's use the following logic. We will choose one of the arguments, let's say x, as the "primary" and will change it from x₀=−R to x_M=R, that is through all values of x_i. For each chosen x=x_i we will choose only those values of y that fall within a circle of radius R, that is from −√R²−x² to √R²−x².

Therefore, while the limits of summation by "primary" argument x are all its values from x₀=−R to x_M=R, the limits of summation by "secondary" argument y depend on the value of "primary" x as specified above.
This dependence of the limits of summation (and, subsequently, integration) by secondary argument on the value of the primary one is the only difference of this case of circular base from the previously considered rectangular base.

Decreasing the intervals between division points by both arguments and going to a limit, we will have, firstly, an integral by a primary argument x in limits from −R to R and, for each value of x we will have to integrate by a secondary argument y in limits that depend on the value of primary argument x - from −√R²−x² to √R²−x².

The final formula would look like this:
∫_−R^R [∫_{−√R²−x²}^√R²−x² f(x, y) dy] dx

Let's use this formula for calculating the volume of a cylinder with f(x, y)=H - the height of a cylinder.
According to the rules of geometry, the volume of a cylinder equals to a product of an area of a base by its height, so we have to get the answer V=πR²H.
Let's check if we get it through integration.

∫_−R^R [∫_{−√R²−x²}^√R²−x² H dy] dx = ∫_−R^R [2H√R²−x²] dx
Substitute
x=R·sin(t),
where −π/2 ≤ t ≤ π/2
Then √R²−x² = R·cos(t),
dx=R·cos(t) dt,
getting
∫_−π/2^π/2[2HRcos(t)]R·cos(t)dt = 2HR²∫_−π/2^π/2cos²(t)dt

To simplify it further, use the trigonometric identity
cos(2t) = cos²(t)−sin²(t) =
= 2cos²(t) −1
from which we derive
cos²(t) = [cos(2t)+1]/2
Our integral now looks like this
2HR²∫_−π/2^π/2[cos(2t)+1]/2 dt =
= HR²∫_−π/2^π/2[cos(2t)+1] dt =
= HR²∫_−π/2^π/2cos(2t) dt + HR²∫_−π/2^π/2 dt
Indefinite integral (anti-derivative) of cos(2t) is (1/2)·sin(2t).
Therefore, the first integral in this sum equals to
∫_−π/2^π/2cos(2t) dt = (1/2)·[sin(2π/2)−sin(−2π/2)] = (1/2)·[sin(π)−sin(−π)] = 0

The second integral in a sum above equals to
∫_−π/2^π/2 dt = π/2 − (−π/2) = π
Therefore, the result of integration is
HR²·π = πR²H which corresponds to results from geometry.

Unizor - Double Integrals - Volume of Solid

Notes to a video lecture on http://www.unizor.com

Double Integrals -
Volume of a Solid

Consider the following problem.
Given a smooth function of two variables f(x, y) (we will always consider smooth functions in terms of continuity and sufficient differentiability), with non-negative values (that is, f(x, y) ≥ 0), defined on a closed rectangle a ≤ x ≤ b, c ≤ y ≤ d and represented by a surface in (X,Y,Z) coordinate space.



In the following we will use the word "area" in a sense of a two-dimensional part of a plane and as a quantitative measure of this part of plane. The context would clarify which one it is used in every case.

Our task is to find the "volume of a solid" - the measure of a part of coordinate space bounded on the top by a surface representing this function, on the bottom - the X,Y-plane and on the four sides by planes x = a, x = b, y = c and y = d.

There is no ready to use formula for such a volume. We do know how the volume of a rectangular parallelepiped is defined, it is a product of its three dimensions - length multiplied by width, multiplied by height, but not of such a complicated figure as the one we consider now.

We really have to define what the volume of this figure is and then attempt to calculate it based on values of function f(x, y) on a rectangle [a, b, c, d].
We did have a similar problem in Geometry with the volume of solids and approached it as a sequence of approximations of a complex figure with simple ones. Let's do the same now.

We will use certain intuitive considerations to define the volume of a solid and will prove that this definition is mathematically valid.

The process of approximation starts with dividing rectangle [a, b, c, d] into many small rectangles by lines x=x_i (where i∈[0,M], x₀=a, x_M=b) and y=y_j(where j∈[0,N], y₀=c, y_N=d) and constructing M·N rectangular parallelepipeds on the base of these small rectangles with the height equaled to a value of function f(x, y) in the corner of each base rectangle with largest coordinates x and y ("top right corner").

If point (x_i, y_j) represents the coordinates of a "top right" corner of a small base rectangle and Δx_i=x_i−x_i−1, Δy_j=y_j−y_j−1are sides of this small rectangle, the volume of a constructed rectangular parallelepiped equals to
ΔV_i,j = f(x_i, y_j)·Δx_i·Δy_j

The combined volume of all these parallelepipeds approximates the volume of our solid. With increasing number of small base rectangles and, correspondingly, decreasing their dimensions we assume that there is a limit of the combined volume of all these parallelepipeds.
It can be proven that under certain conditions of smoothness of our function f(x, y) the limit does exist and is unique, regardless of the way how exactly we divide the domain of our function into small rectangles, as long as their dimensions are converging to zero (or, more precisely, the =dimensions of the largest among them converges to zero).

Now let's consider how we can summarize the volumes of all parallelepipeds constructed on the basis of small rectangles. There are two simple methods.

1. We can go from one point y=y_j to another, varying index j from 1 to N and for each value of y=y_j summarize the volumes of all parallelepipeds based on all values of x=x_i, varying index i from 1 to M. So, for each index j we calculate the sum of all V_i,j, varying index i.
Then we summarize these sums by index j deriving with an approximate volume
V_M·N = Σ_j∈[1,N] Σ_i∈[1,M] V_i,j =
= Σ_j Σ_i f(x_i, y_j)·Δx_i·Δy_j =
= Σ_j [Σ_i f(x_i, y_j)·Δx_i]·Δy_j

2. On the other hand, we can go from one point x=x_i to another, varying index i from 1 to M and for each value of x=x_isummarize the volumes of all parallelepipeds based on all values of y=y_j, varying index j from 1 to N. So, for each index i we calculate the sum of all V_i,j, varying index j.
Then we summarize these sums by index i deriving with an approximate volume
V_M·N = Σ_i∈[1,M] Σ_j∈[1,N] V_i,j =
= Σ_i Σ_j f(x_i, y_j)·Δx_i·Δy_j =
= Σ_i [Σ_j f(x_i, y_j)·Δy_j]·Δx_i

Both approaches to summarizing the volumes of small parallelepipeds should result in the same value of a combined volume.

Let's examine now what happens with both our formulas for total volume when the rectangles are getting smaller and smaller.

Recall the definition of a definite integral of function φ(t) on a segment p ≤ t ≤ q as a limit of sums of areas of rectangles obtained by dividing segment [p,q] into small pieces:
Σ_k φ(t_k)·Δt_k → ∫_p^q φ(t) dt

We can now say that
Σ_j f(x_i, y_j)·Δy_j converges to
φ(x_i) = lim Σ_j f(x_i, y_j)·Δy_j =
= ∫_c^d f(x_i, y) dy
under condition of maximum among Δy_j converges to zero. Then we continue with the second summation getting
Σ_i [Σ_j f(x_i, y_j)·Δy_j]·Δx_i →
→ Σ_i [∫_c^d f(x_i, y) dy]·Δx_i →
→ ∫_a^b[∫_c^d f(x_i, y) dy] dx

On the other hand, we can similarly state that
Σ_i f(x_i, y_j)·Δx_i converges to
ψ(y_j) = lim Σ_i f(x_i, y_j)·Δx_i =
= ∫_a^b f(x, y_j) dx
under condition of maximum among Δx_i converges to zero. Then we continue with the second summation getting
Σ_j [Σ_i f(x_i, y_j)·Δx_i]·Δy_j →
→ Σ_j [∫_a^b f(x, y_j) dx]·Δy_j →
→ ∫_c^d[∫_a^b f(x, y) dx] dy

But these are supposed to be the same results since the difference is only in the order of summation. The sums are the same, therefore the limits are the same, therefore we can write this limit as a double integral:
∫_c^d∫_a^b f(x, y) dx dy
or
∫_a^b∫_c^d f(x, y) dy dx

Both are the same and constitute two integrations of function f(x, y) performed consecutively, either by x from a to b (keeping y as a constant) and then by y from c to d or, in reverse, first by y from c to d (keeping x as a constant) and then by x from a to b.