Unizor - Double Integrals - Volume of Solid

Notes to a video lecture on http://www.unizor.com

Double Integrals -
Volume of a Solid

Consider the following problem.
Given a smooth function of two variables f(x, y) (we will always consider smooth functions in terms of continuity and sufficient differentiability), with non-negative values (that is, f(x, y) ≥ 0), defined on a closed rectangle a ≤ x ≤ b, c ≤ y ≤ d and represented by a surface in (X,Y,Z) coordinate space.



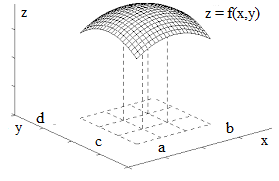
In the following we will use the word "area" in a sense of a two-dimensional part of a plane and as a quantitative measure of this part of plane. The context would clarify which one it is used in every case.

Our task is to find the "volume of a solid" - the measure of a part of coordinate space bounded on the top by a surface representing this function, on the bottom - the X,Y-plane and on the four sides by planes x = a, x = b, y = c and y = d.

There is no ready to use formula for such a volume. We do know how the volume of a rectangular parallelepiped is defined, it is a product of its three dimensions - length multiplied by width, multiplied by height, but not of such a complicated figure as the one we consider now.

We really have to define what the volume of this figure is and then attempt to calculate it based on values of function f(x, y) on a rectangle [a, b, c, d].
We did have a similar problem in Geometry with the volume of solids and approached it as a sequence of approximations of a complex figure with simple ones. Let's do the same now.

We will use certain intuitive considerations to define the volume of a solid and will prove that this definition is mathematically valid.

The process of approximation starts with dividing rectangle [a, b, c, d] into many small rectangles by lines x=x_i (where i∈[0,M], x₀=a, x_M=b) and y=y_j(where j∈[0,N], y₀=c, y_N=d) and constructing M·N rectangular parallelepipeds on the base of these small rectangles with the height equaled to a value of function f(x, y) in the corner of each base rectangle with largest coordinates x and y ("top right corner").

If point (x_i, y_j) represents the coordinates of a "top right" corner of a small base rectangle and Δx_i=x_i−x_i−1, Δy_j=y_j−y_j−1are sides of this small rectangle, the volume of a constructed rectangular parallelepiped equals to
ΔV_i,j = f(x_i, y_j)·Δx_i·Δy_j

The combined volume of all these parallelepipeds approximates the volume of our solid. With increasing number of small base rectangles and, correspondingly, decreasing their dimensions we assume that there is a limit of the combined volume of all these parallelepipeds.
It can be proven that under certain conditions of smoothness of our function f(x, y) the limit does exist and is unique, regardless of the way how exactly we divide the domain of our function into small rectangles, as long as their dimensions are converging to zero (or, more precisely, the =dimensions of the largest among them converges to zero).

Now let's consider how we can summarize the volumes of all parallelepipeds constructed on the basis of small rectangles. There are two simple methods.

1. We can go from one point y=y_j to another, varying index j from 1 to N and for each value of y=y_j summarize the volumes of all parallelepipeds based on all values of x=x_i, varying index i from 1 to M. So, for each index j we calculate the sum of all V_i,j, varying index i.
Then we summarize these sums by index j deriving with an approximate volume
V_M·N = Σ_j∈[1,N] Σ_i∈[1,M] V_i,j =
= Σ_j Σ_i f(x_i, y_j)·Δx_i·Δy_j =
= Σ_j [Σ_i f(x_i, y_j)·Δx_i]·Δy_j

2. On the other hand, we can go from one point x=x_i to another, varying index i from 1 to M and for each value of x=x_isummarize the volumes of all parallelepipeds based on all values of y=y_j, varying index j from 1 to N. So, for each index i we calculate the sum of all V_i,j, varying index j.
Then we summarize these sums by index i deriving with an approximate volume
V_M·N = Σ_i∈[1,M] Σ_j∈[1,N] V_i,j =
= Σ_i Σ_j f(x_i, y_j)·Δx_i·Δy_j =
= Σ_i [Σ_j f(x_i, y_j)·Δy_j]·Δx_i

Both approaches to summarizing the volumes of small parallelepipeds should result in the same value of a combined volume.

Let's examine now what happens with both our formulas for total volume when the rectangles are getting smaller and smaller.

Recall the definition of a definite integral of function φ(t) on a segment p ≤ t ≤ q as a limit of sums of areas of rectangles obtained by dividing segment [p,q] into small pieces:
Σ_k φ(t_k)·Δt_k → ∫_p^q φ(t) dt

We can now say that
Σ_j f(x_i, y_j)·Δy_j converges to
φ(x_i) = lim Σ_j f(x_i, y_j)·Δy_j =
= ∫_c^d f(x_i, y) dy
under condition of maximum among Δy_j converges to zero. Then we continue with the second summation getting
Σ_i [Σ_j f(x_i, y_j)·Δy_j]·Δx_i →
→ Σ_i [∫_c^d f(x_i, y) dy]·Δx_i →
→ ∫_a^b[∫_c^d f(x_i, y) dy] dx

On the other hand, we can similarly state that
Σ_i f(x_i, y_j)·Δx_i converges to
ψ(y_j) = lim Σ_i f(x_i, y_j)·Δx_i =
= ∫_a^b f(x, y_j) dx
under condition of maximum among Δx_i converges to zero. Then we continue with the second summation getting
Σ_j [Σ_i f(x_i, y_j)·Δx_i]·Δy_j →
→ Σ_j [∫_a^b f(x, y_j) dx]·Δy_j →
→ ∫_c^d[∫_a^b f(x, y) dx] dy

But these are supposed to be the same results since the difference is only in the order of summation. The sums are the same, therefore the limits are the same, therefore we can write this limit as a double integral:
∫_c^d∫_a^b f(x, y) dx dy
or
∫_a^b∫_c^d f(x, y) dy dx

Both are the same and constitute two integrations of function f(x, y) performed consecutively, either by x from a to b (keeping y as a constant) and then by y from c to d or, in reverse, first by y from c to d (keeping x as a constant) and then by x from a to b.