UNIZOR.COM - Physics4Teens - Electromagnetism - The Laws of Induction - Wire Frame Rotation

Notes to a video lecture on http://www.unizor.com

Wire Frame Rotation

Let's start with a summary of our knowledge about electromagnetic induction before embarking on a rotation of a wire frame in a magnetic field.

The foundation of electromagnetic induction is the Lorentz force that is exerted by a magnetic field onto an electrically charged particle moving across the magnetic field lines.

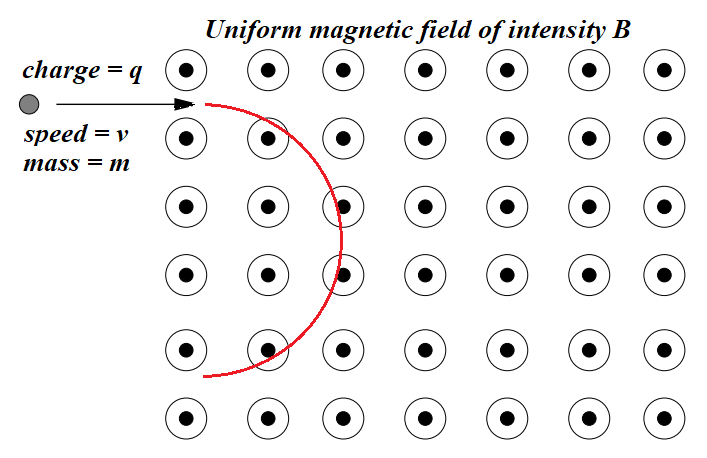
As we demonstrated in previous lectures, this force equals to
F = q·V·B
where
q is the particle's electric charge,
V is the speed of this charge in a direction perpendicular to magnetic field lines (if it's not perpendicular, it should be multiplied by sin(φ), where φ is an angle between a velocity vector of a particle and magnetic field lines),
B is the intensity of a magnetic field.
In vector form, considering general direction of a particle's velocity and magnetic field intensity vector, the formula is
F =q·V ⨯ B  
The important fact about the Lorentz force, acting on an electrically charged moving particle (like an electron) is that it acts perpendicularly to both velocity of a particle and the magnetic field intensity vectors.

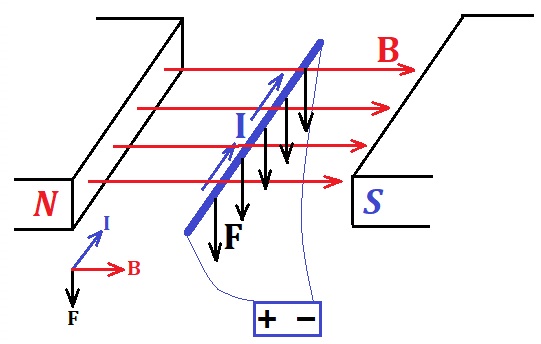
When we move a metal rod parallel to itself and perpendicularly to magnetic field lines, "free" electrons are pulled by this motion towards the general direction of a rod (green arrow on a picture below).
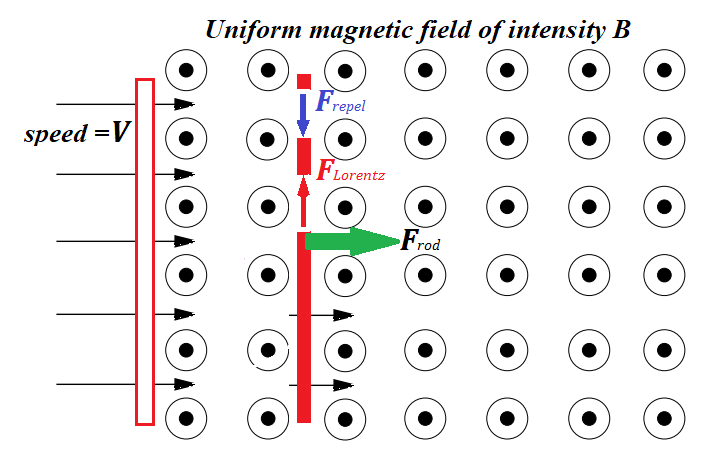
This movement of electrons is perpendicular to magnetic field lines and, therefore, is a subject to Lorentz force that pushes electrons perpendicularly to a general direction of a rod's movement and perpendicularly to magnetic field lines, that is electrons are pushed along the rod to its edge (red vertical arrow on a picture above).

This generates the difference of electric potential on the opposite ends of a rod, one will be positive, another - negative. The faster we move the rod - the stronger Lorentz force is - the greater difference of electric potential will be generated.

The Lorentz force that pushes the electrons to the end of a moving rod meets the resistance of electrostatic forces that repel electrons from each other (blue vertical arrow on a picture above). That's why the concentration of "free" electrons at one end of a rod that moves with certain speed reaches its maximum and stays this way. For every speed of movement of a rod and a particular magnetic field intensity there is a specific difference of potentials or electromotive force (EMF) developed at the ends of a rod.

Let's connect the ends of our rod, that accumulated positive and negative charges as a result of the Lorentz force on moving "free" electrons, through any consumer of electricity, like a lamp.

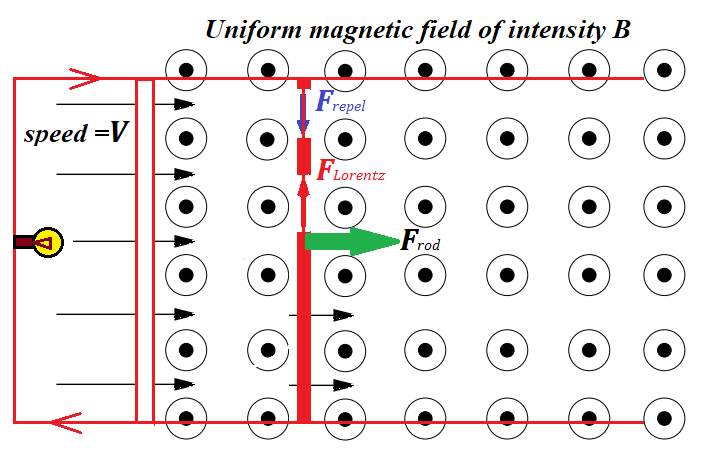
The accumulated excess of electrons from one end of a rod will go to the connecting wire to a lamp and to the positively charged end of a rod. This will diminish a concentration of electrons on a negative end of a rod. While a rod continues its movement across the magnetic field, the Lorentz force acting on "free" electrons inside a rod will push more electrons to the end to replace those that went through a lamp to a positive end of a wire, thus establishing a constant electric current in an electric circuit, generated by mechanical movement of a rod perpendicularly to magnetic field lines.

From the first glance it looks like movement of a rod with constant speed, which does not require any energy to spend, generates electricity and, therefore, free energy, which contradicts the Law of Conservation of Energy. What do we miss?

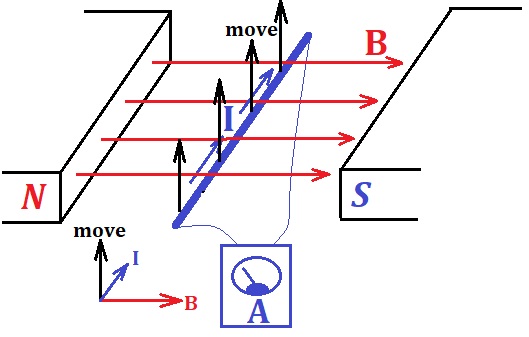
Let's make one more step in our analysis of this experiment. The electric current generated by a rod's movement runs around a circuit and, therefore, runs through a rod as well perpendicularly to magnetic field lines. As we know, the wire with electric current perpendicular to magnetic field lines experiences another manifestation of the Lorentz force - the one that pushes the whole rod perpendicularly to its length.

The Lorentz force analyzed first acts on electrons moving with a rod to the right on the picture above and pushes them to one end of a rod (upwards on the picture). This creates an electric current in a rod, and the Lorentz force, acting on electrons moving along the rod pushes them and the whole rod with them to the left against the initial movement of a rod, thus forcing the need for some outside force to move the rod with constant speed.

As we see, a magnetic field acts against the movement of a rod.
It means, to move a rod, we have to overcome the resistance and perform some work. This work, according to the Law of Energy Conservation, is converted in some other type of energy, like into heat in the lamp on a circuit.

If we follow the trajectory of "free" electrons inside a rod, we would see that they move simultaneously in two directions - to the right with rod's movement and upwards because of the Lorentz force acting on moving particles in a magnetic field perpendicularly to the field's intensity vector.

In vector form the velocity vector of an electron can be represented as
V_e = V_r + V_u
where
V_e is velocity of an electron,
V_r is its velocity to the right,
V_u is its velocity upwards.

Therefore, the total Lorentz force is
F =q·(V_r +V_u )⨯ B   =
= q·V_r ⨯ B + q·V_u ⨯ B   =
= F_u + F_l  
where
F_u  is upward component of the Lorentz force that pushes electrons towards the end of a rod,
F_l   is its component to the left against the rod's motion.

The electromotive force (EMF) generated by the movement of a rod was quantitatively evaluated in the previous lecture. As the rod moves to the right, thus increasing the length of two sides of a circuit's rectangular frame, the magnitude of a generated EMF was equal to the rate of a change of a magnetic field flux through the frame:
|U| = |dΦ/dt|
where the magnetic field flux was defined as a product of magnetic field intensity B and the area of a wire frame evaluated in a direction perpendicular to the magnetic field lines.
This is the Faraday's Law of electromagnetic induction.

To better understand a concept of magnetic field flux we can use a concept of the "number" of magnetic field lines. These lines point toward the direction of magnetic field forces and their density represents the strength of these forces. Using this concept, magnetic field flux is analogous to the "number" of magnetic field lines going through a wire frame. Wider wire frame, more intense magnetic field - greater magnetic field flux goes through the wire frame.

That concludes the summary of our knowledge about electromagnetic induction, as presented so far, and we are ready to switch to a more practical way of generating the electricity from mechanical movement - from a rotation of a wire frame.

Considering it's impractical to change the magnetic flux by changing the geometry of a wire frame, a different approach to generate electricity was suggested - to rotate a wire frame. Rotating it, we change the angle between the wire frame plane and the magnetic field lines, thus changing the magnetic flux going through a frame.
Let's examine closer this process.

Consider a rotation of a wire frame with dimensions a by b, rotating with a constant angular speed ω in the uniform magnetic field B.



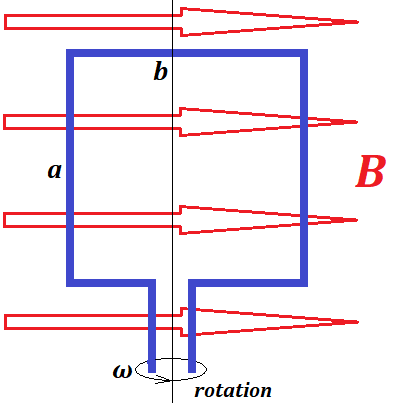
Consider the initial position of a wire frame to be, as shown on a picture above, with an axis of rotation perpendicular to magnetic field lines and side b of a frame parallel to magnetic field lines. Then side a would be perpendicular to magnetic field lines.
As the frame rotates with an angular speed ω, the angle of a side b with the lines of a magnetic field, as a function of time, is
φ(t) = ω·t

Side b of a wire frame and its opposite do not sweep across magnetic field lines, only side a and its opposite do.
Side a and its opposite are crossing magnetic field lines in opposite directions. Viewing in the direction of the magnetic field lines, if side a crosses the magnetic field lines from right to left, the opposite side at the same time crosses these magnetic lines left to right.

As the wire frame rotates, the "free" electrons inside side a and its opposite are pushed by the rotation of a wire across the magnetic field lines in opposite directions and, therefore, are pushed by the Lorentz force, exerted by a magnetic field on these electrons, towards opposite ends of corresponding sides of wire frame. If electrons in side a are pushed upwards, the electrons in the opposite side are pushed downwards and vice versa.
As a result, there is an electric current generated in a rotating wire frame.

When a wire crosses the magnetic field lines with "free" electrons inside, Lorentz force on electrons inside the wire is proportional to a speed of a wire across the magnetic field lines in a direction perpendicular to these lines. Consequently, the faster a wire is crossing the magnetic field lines in a perpendicular to them direction - the more electric charge inside a wire is separated between positive and negative ends. Therefore, the electric current generated by the movement of a wire across the magnetic field lines is proportional to a speed of perpendicularly crossing these lines.

At its original position at time t=0 side a crosses more magnetic field lines per unit of time than at position of a wire frame turned by 90°. The "number" of magnetic field lines crossed per unit of time is maximum at angle φ(t)=0 and minimum (actually, zero) at φ(t)=π/2.
As the wire frame continues its rotation, the "number" of magnetic field lines crossed per unit of time increases and reaches another maximum at φ(t)=π, then diminishes to zero at φ(t)=3π/2.

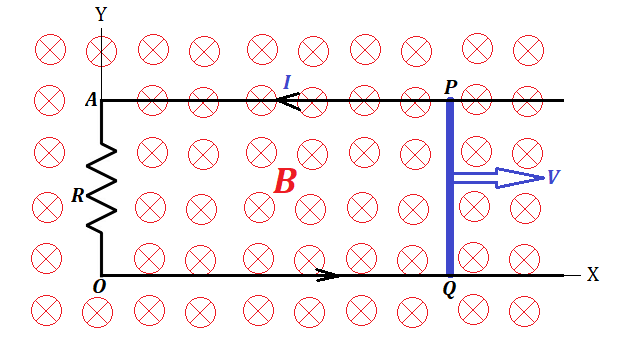
To calculate the speed of crossing the magnetic field lines in a perpendicular to them direction by sides a and its opposite, consider a top view onto our wire frame.

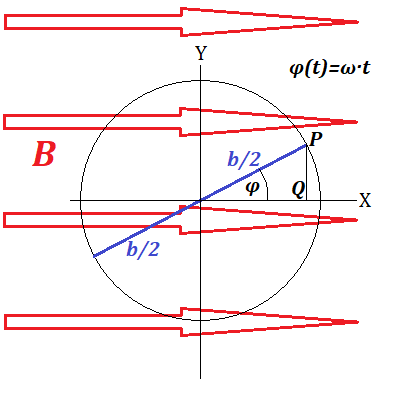
Side a and its opposite are circulating around the axis of rotation on a radius b/2. During time t the angle of rotation will be φ(t)=ω·t.

The speed of crossing the magnetic field lines by side a or its opposite is a Y-component of a velocity vector of the points P or its opposite.

The Y-coordinate of point P is
PQ = b·sin(φ)/2 = b·sin(ω·t)/2.
Therefore, the Y-component of a vector of velocity of point P is a derivative of this function
V_Y = b·ω·cos(ω·t)/2.

Analyzing this expression, we quantitatively confirm our considerations about speed of crossing the magnetic field lines presented above.
At t=0 this function is at maximum and equals to b·ω/2 - linear speed of a point-object rotating with angular speed ω on a radius b/2.
At t=90° the value of V_Y is zero because the point P moves parallel to X-axis.
Than the Y-component of velocity goes to negative part, crossing the magnetic field lines in an opposite direction etc.
During one full rotation the direction of an electric current in a wire frame will change because each side half of a circle crosses the magnetic field lines in one direction and on another half of a circle crosses them in an opposite direction. This is how alternate current is produced by electric power plants.

As Lorentz force on "free" electrons within side a separates them from their atoms and pushes to one end of this side, Lorentz force on the opposite side of a frame performs similar action, separating electrons towards the opposite end of a wire, thus assuring the electrical current inside a wire frame I=I(t).

Rotation of side a and its opposite can be represented as simultaneous movement along two coordinates. Movement along X-axis, as presented on a picture above, does not cross magnetic field lines, there is no Lorentz force related to this movement, no separation of electrons from their nuclei, no EMF.
But movement along Y-axis does cross magnetic field lines and, therefore, the Lorentz force pushes electrons to one end of a wire and resists the rotation by acting against the movement along the Y-axis.
As we have an electric current I(t) inside a wire frame, there is a Lorentz force acting upon side a and its opposite that needs to be overcome to assure the rotation with constant angular speed ω.

The force on side a directed against its movement along the Y-axis is
F_a(t) = I(t)·a·B
and the same by magnitude force, but acting upon a side opposite to a, also against its movement along Y-axis.
Both these forces are acting against the rotation. When side a moves in the positive direction of the Y-axis, the force F_a(t) is directed towards the negative one and vice versa. Same with the side opposite to side a.

The key consideration now is the following.
The force F_a(t) and its opposite must be overcome by a rotation, that is some work must be exerted by a rotating mechanism, which, according to the Law of Energy Conservation, must be equal to amount of work the generated electric current exerts by circulating in the wire frame.
That is, mechanical work of rotation is converted into electrical work - electric power is generated by a rotation.

The Y-coordinate of point P, rotating around the origin of coordinates with an angular speed ω on a radius b/2, as a function of time t, is
P_Y(t) = b·sin(ω·t)/2
The Y-component of a velocity vector of point P is a derivative of this function
V_Y(t) = b·ω·cos(ω·t)/2

During the time from t to t+dt point P and, therefore, side a will be moved by a rotation in the Y-direction by a distance
dS_Y = V_Y(t)·dt =
= b·ω·cos(ω·t)·dt/2
Therefore, the work needed to overcome the force F_a(t), acting in the direction of Y-axis against the rotation of side a, during the time from t to t+dt is
dW_a = F_a(t)·V_Y(t)·dt =
= [I(t)·a·B]·b·ω·cos(ω·t)·dt/2

The same by magnitude and opposite in direction force acts on a side opposite to a, also acting against its movement in the direction of the Y-axis. Therefore, the increment of work needed to be exerted by a rotation mechanism to assure the rotation at angular speed ω, as a function of time t during the time from t to t+dt is
dW = [I(t)·a·B]·b·ω·cos(ω·t)·dt

The power exerted by a rotating mechanism at time t is
P(t) = dW/dt =
= I(t)·a·B·b·ω·cos(ω·t)

During this period from t to t+dt the electricity generated by the rotation of the wire has the value of current equal to I(t). The cause of this current is the electromotive force (EMF) or, simply, voltage U(t) generated by Lorentz force on "free" electrons that separates them from their atoms.

The power exerted by an electric current I with voltage U is P=I·U.
Equating this power of electric current to a power exerted by a rotating mechanism, as the Law of Energy Conservation dictates, we obtain
I(t)·a·B·b·ω·cos(ω·t) = I(t)·U(t)
From this we can find EMF generated by a rotation of a wire frame:
U(t) = B·a·b·ω·cos(ω·t)
Applying simple geometry, we can see that the area of a wire frame perpendicular to magnetic lines at time t equals to
S(t) = a·b·sin(ω·t)
Therefore, magnetic field flux through the wire frame at time t is
Φ(t) = B·a·b·sin(ω·t)
The rate of change of this flux is, therefore, a derivative
dΦ(t)/dt = B·a·b·ω·cos(ω·t)

Comparing this with the above expression for EMF, we see that
U(t) = dΦ(t)/dt
which is the same as in a case of a rod moving parallel to itself on rails perpendicularly to the magnetic field lines, discussed in the prior lecture.
This brings us to an important generalization of the Faraday's Law.
If the magnetic flux going through a wire loop is changing, the rate of this change equals to an electromotive force generated inside a wire.

UNIZOR.COM - Physics4Teens - Electromagnetism - The Laws of Induction - ...

 



Notes to a video lecture on http://www.unizor.com



Faraday's Law of

Electromagnetic Induction



Let's consider an experiment we described in a lecture about Lorentz
force exerted by a uniform magnetic field onto a wire with an electric
current running through it.



On this picture the density of magnetic field lines (red arrows)
represents the intensity of this field. If, for example, one line per
square centimeter of an area perpendicular to the direction of magnetic
field lines means the field of intensity 0.001T (i.e. 1/1000 of tesla), the density of 10 such lines per square centimeter signifies the intensity 0.01T (i.e. 1/100 of tesla).

In this lecture we will use an expression "the number of magnetic field
lines" in a context of a wire crossing them or sweeping across them. It
only means to demonstrate that the intensity of a magnetic field should
participate in our logic, formulas and calculations as a factor
proportional to a perpendicular to magnetic lines area, crossed or swept
across.



Recall that the Lorentz force exerted by a uniform magnetic field onto a
wire with an electric current running through it for any angle φ between the electric current in a wire and magnetic field lines equals to

F = I·L·B·sin(φ)

where

I is the amperage of an electric current running through a wire,

L is the length of a wire,

B is the strength of an external magnetic field

φ is the angle between the direction of the electric current and lines of an external magnetic field



Taking into consideration the direction of the Lorentz force
perpendicular to both vectors - electric current and lines of an
external uniform magnetic field, the above formula can be represented
using a vector product

F = I ·L⨯ B  



In a simple configuration of the magnetic field and wire on a picture above φ=90° and the formula for a magnitude of a Lorentz force looks like

F = I·L·B



From the microscopic viewpoint the magnetic field exerts a Lorentz force
onto each electron moving inside the wire as a part of the electric
current. This force is perpendicular to both magnetic field lines and
the electric current in a wire and, consequently, causes the motion of
an entire wire.

If an electric current in a wire is produced by a charge q passing through a wire of length L during time t, thus making the electric current equal to I=q/t with the speed of moving V=L/t, the formula for Lorentz force acting on this charge becomes

F = I·L·B = (q/t)·(V·t)·B =

= q·V·B



The cause of the electric current in a wire and, therefore, motion of
electrons in one direction in the experiment above is some voltage or electromotive force (EMF) applied to wire's ends. So, the voltage or EMF at wire's ends causes the current in it and, consequently, its movement.

But what happens if we attempt to reverse the cause and effect and move the wire ourselves without any voltage applied to it?

Will the voltage be generated?



Consider a similar experiment, but no initial current running through a
wire. Instead, the wire is connected to an ammeter to measure the
intensity of the electric current running through it, thus making a
closed electric circuit.



Let's move the wire in the upward direction as indicated on a picture.
The experiment shows that, while the wire is moving across the magnetic
field lines, there is an electric current in it.

Let's examine the reason why it happens.



There are positively charged nuclei of atoms relatively fixed in their
position by inter-atomic forces and there are electrons rotating around
these nuclei in each atom on different orbits. Usually, one or two
electrons from the outer orbits are relatively free to drift or exchange
their atom hosts. These "free" electrons are moving together with the
wire.



As we investigated the motion of charged particles in a magnetic field,
we came to a conclusion that there is a force acting on these charged
particles (electrons in our case) directed perpendicularly to their
trajectory - the Lorentz force.



Moving the wire across the magnetic field lines (upwards on a picture
above) results in the Lorentz force to act on "free" electrons, which
causes electrons to move in the direction of the Lorentz force
perpendicularly to their trajectory, while still being inside a wire.
So, they will move to one side of a wire, generating the difference in
charges on the wire's ends, that is generating the difference in
electric potentials or voltage or electromotive force (EMF).
If we have a loop with this wire being a part of it (like on a picture
with an ammeter in a loop), there will be an electric current in a wire.



As we see, the movement of a wire across the magnetic field lines generates a difference in electric potentials or an electromotive force (EMF) and, if there is a closed loop, an electric current in a wire. This is called electromagnetic induction.



Let's quantify the voltage (or electromotive power - EMF)
generated by a straight line wire moving in a uniform magnetic field
parallel to itself in a plane perpendicular to magnetic field lines.



In a setup presented on the above picture the straight line wire PQ is moving parallel to itself and parallel to Y-axis along the rails AP and OQ stretched parallel to X-axis and connected by a resistor R, making a closed circuit with a wire PQ being a part of it.



The uniform magnetic field of intensity B is directed along the Z-axis perpendicularly to XY-plane in a direction of viewing the picture.



"Free" electrons, carried by a wire's motion along X-axis, experience
the Lorentz force directed perpendicularly to their movement inside a
wire, that is they will move to one end of a wire. The Lorentz force
acting on each such electron equals to (see Problem 1c in "Magnetic Field" topic of this course)

F_L = e·V·B

where

e is an electric charge of an electron that is able to "freely" move,

V is the speed a wire moving along the X-axis,

B is the intensity of the magnetic field.



As a result, the difference in electric potential (or EMF) is generated and an electric current I will start running in the closed circuit OAPQ.

So, Lorentz force on electrons moving with a wire along the X-axis
causes the electrons to move to one end of a wire, that causes the
electric current in the wire. The latter causes the force exerted by the
magnetic field onto a wire in the direction opposite to its movement.



Since we are moving the wire ourselves with constant speed V
towards the positive direction of X-axis, we have to exert work against
the force of magnetic field onto a wire directed in the negative
direction.



This force of magnetic field onto a wire directed in the negative direction equals, as we mentioned above, to

F = I·L·B

where L is the length of a wire PQ.

If during time t the wire moves by a distance S=V·t, the work we have to do against the force F equals to

W = F·S = I·L·B·V·t

To do this work during a time interval t, we have to exert a power

P = W/t = F·S = I·L·B·V



Energy does not disappear without a trace. In this case the energy we spend generated voltage (EMF) U at wire's ends and an electric current I in a closed circuit. It will be transformed into heat in the resistor R with a rate I·U.

Therefore, we can equate two powers - the one we exerted to move a wire and the one consumed by a resistor:

I·L·B·V = I·U

from which we obtain the amount of EMF generated by moving the wire

U = L·V·B



Let's examine the expression on the right.

The value L·V represents the rate of increase of the area of a circuit OAPQ per unit of time.

The product of the area and the intensity of the magnetic field with
magnetic field lines going through this area perpendicularly to it is
called magnetic flux Φ.

Since our magnetic field is uniform, an expression L·V·B represents the rate of increase of magnetic flux, which we can safely denote using the language of calculus as dΦ/dt.



In this language we can state that the electromotive force (EMF) generated by a moving wire - a part of a closed circuit - equals to a rate of increase of magnetic flux going through this closed circuit.

U = dΦ/dt.

This is the Faraday's Law of electromagnetic induction.

UNIZOR.COM - Physics4Teens - Electromagnetism - Magnetism and Electric C...

Notes to a video lecture on http://www.unizor.com



Parallel Currents - Problems 2



IMPORTANT NOTES



Recall the Lorentz force exerted by a magnetic field B (a vector) onto straight line electric current I (also a vector) of length L

F = I ·L⨯ B

The magnitude of this force can be expressed in terms of magnitudes of
the vectors of electric current and magnetic field, taking into
consideration an angle θ between them:

F = I·L·B·sin(θ)

In case electric current and magnetic field vectors are perpendicular to each other it looks as

F = I·L·B

The last formula will be used in this levture.



Also, as we know from previous lectures, the magnetic field force lines
around a long thin straight line wire with electric current I
running through it are circular in planes perpendicular to a wire and
centered at the points of the wire. Their direction is determined by a
corkscrew rule or the rule of the right hand.

On a distance R from the wire the vector of intensity of a magnetic field produced by this wire has a magnitude

B = μ₀·I/(2π·R)

where μ₀ is a constant permeability of vacuum.



The direction of this force vector at any point of space around a wire
corresponds to the direction of the circular magnetic field line going
through this point and is tangential to this magnetic line.



Problem 2A

Two ideally long and thin straight wires are parallel to each other and positioned at distance d from each other.

One wire carries an electric current of amperage I₁.

Another wire carries an electric current of amperage I₂ in the opposite direction.

Determine the magnitude of the repelling force between these two wires per unit of length of each.



Solution



Consider the first wire as having an infinite length, while the second one to have a finite length L.

The magnetic field of the first wire at each point of the second wire can be considered as uniform, having a magnitude

B₁ = μ₀·I₁/(2π·d)

According to the formula for a force exerted by a uniform magnetic field
onto a wire with electric current that is perpendicular to the force of
magnetic field, the repelling Lorentz force exerted by the first wire
onto the second one is

F₁₂ = I₂·L·B₁ =

= μ₀·I₁·I₂·L /(2π·d)

If we calculate this force per unit of length of the second wire, the result is

F₁₂ = μ₀·I₁·I₂ /(2π·d)



Now consider a second wire as having an infinite length, while the first one to have a length L.

All previous results are applicable to this reverse logic, and we can
determine the magnitude of the repelling Lorentz force exerted by the
second wire per unit of length of the first

F₂₁ = μ₀·I₁·I₂ /(2π·d)

It's also a repelling force, so it's direction is opposite to F₁₂.



It's not coincidental that the forces F₁₂ and F₂₁ are equal in magnitude, since it corresponds to the Third Newton's Law.



Problem 2B

Two identical sufficiently long and thin straight wires of mass m per unit of length are horizontally hanging on threads of the same length L parallel to each other at the same height. The initial distance between them is d and they can swing on their corresponding threads parallel to themselves.

Initially there is no current in these wires and the threads holding these wires are in vertical position.

When we run electric current I through the first wire and the same in amperage electric current I through the second one in the opposite direction, the wires swing away from each other on their threads.

At equilibrium both threads made an angle φ with a vertical.

Determine the amperage I.



Solution

The following picture represents the view along the direction of wires
before and after the electric currents in both wires are turned on.


The wires are represented as circles. Before the electric current is
turned on the circles are white. When the electric current is on, the
circles are blue and red to represent the opposite directions of the
electric current in these wires.



Let T be the tension of a thread per unit length of a wire.

A vertical component of the thread tension per unit length of a wire T·cos(φ) balances the weight of the unit length of a wire m·g, which can be expressed as an equation

T·cos(φ) = m·g

from which we derive

T = m·g/cos(φ)



A horizontal component of the thread tension per unit length of a wire T·sin(φ) is supposed to balance the magnetic field repelling force, which has been calculated in the above Problem 2A as

F₁₂ = μ₀·I₁·I₂ /(2π·d)

except in our case

I₁ = I₂ = I

and, instead of the distance d we have to use D=d+2L·sin(φ) - the final distance between the wires at the point of equilibrium.

The result is

T·sin(φ) = μ₀·I² /(2π·D)

from which follows

I² = 2π·D·T·sin(φ)/μ₀ =

= 2π·D·m·g·sin(φ)/(μ₀·cos(φ)) =

= 2π·D·m·g·tan(φ)/μ₀

This gives the amperage of the current equal to

I = √2π·D·m·g·tan(φ)/μ₀

where D = d+2L·sin(φ)

Unizor - Physics4Teens - Electromagnetism - Magnetism and Electric Curre...

Notes to a video lecture on http://www.unizor.com



Two Parallel Straight Line Currents



Let's examine a behavior of two ideally long and thin parallel wires, each carrying an electric current.



Two wires carrying an electric current are blue and brown on this picture.

As we know, since the wires carry electric current, there is a magnetic
field around each of these wires. It has circular form, as presented on a
picture above in corresponding colors. The direction of the magnetic
field lines is determined by the corkscrew rule or the right hand rule and is shown on the picture.



Each circular magnetic field line around the blue wire and any
tangential to it, that is the vector of magnetic force, belong to a
plane perpendicular to this wire. Since the brown wire is parallel to
the blue one, any tangential to any magnetic field line of the blue wire
is perpendicular to the brown wire.



Since the brown wire's electric current is perpendicular to the
direction of the magnetic field lines of the field produced by the blue
wire, the brown wire is under the Lorentz force produced by the magnetic
field of the blue wire. Using the right hand rule for the brown
wire and blue magnetic field lines, we determine the direction of this
Lorentz force. It appears to be directed from the brown wire towards the
blue one.



The wires are in symmetrical positions, so exactly the same logic can be
applied to the blue wire in the magnetic field of the brown wire. As a
result, the Lorentz force produced by the magnetic field of the brown
wire attracts the blue wire towards the brown one.



Now we see that both wires attract each other, which is caused by the
Lorentz force exerted on each of them from the magnetic field of the
other one.



Let's arrange a similar experiment having electric currents in the wires
to go in opposite directions. Let the blue wire's current to go the
same way as on the picture above, that is upward, but the direction of
the electric current in the brown wire to be downward.

The logic about circular magnetic field lines around any wire and
perpendicularity of the electric current of one wire to the magnetic
field lines of the opposite one remains the same. The only difference is
that, when we apply the right hand rule to determine the
direction of the Lorentz force, the result will be opposite than before,
the Lorentz force will push the brown wire away from the blue one.



Analogous result will be when we consider the electric current in the
blue wire in the magnetic field of the brown wire. The Lorentz force in
this case will also be repelling.



The conclusion of these experiments is that

(a) parallel wires carrying electric charge will attract each other if the currents are in the same direction;

(b) parallel wires carrying electric charge will repel each other if the currents are in the opposite directions.



This effect was studied by Ampere and the mutual attraction or repulsion
of two parallel wires carrying an electric current is often referred to
as the Ampere force.



Contemporary definition of an 1 ampere (1A) as a unit of electric current is 1 coulomb per 1 second (1C/1sec) with a unit of charge 1 coulomb defined based on the charge of certain number of electrons.



At the time of Ampere's experiments with parallel wires scientists did
not know about electrons and could not measure the electric current in
the same terms as we do now.

But Ampere's experiments have opened the way to measure the electric
current by measuring the purely mechanical characteristic of the force
of attracting or repelling between the wires carrying the electric
current. So, the first definition of a unit of current was based on
measuring the Ampere force between the two wires.



Here is a simple description of how the electric current can be measured (not necessarily the method used by Ampere).



Let two identical wires hang horizontally parallel to each other on threads of the same length from the same height.

Without an electric current running through them these wires hang on vertical threads.



When we apply voltage to both of them from the same battery, the
electric current in each of them produces the magnetic field that will
cause their mutual attraction or repelling, and the threads holding the
wires would deviate from their vertical position. The angle of deviation
can be measured and it can be used to determine the force of attraction
or repelling between the wires.



So, knowing the unit of length and the unit of force, 1 ampere (1A),
as a unit of electric current, can be defined as the electric current
that produces a unit of force per unit of length of a wire, when this
wire is positioned at a unit of length distance from another wire with
the same electric current.



That was the original method of definition of the unit of electrical
current. At the time it was using old units of length and force.

Later on the definition was slightly changed using concepts of
infinitely long and infinitesimally thin wires (to avoid irregularities
of the magnetic field) and contemporary measures of length (meter) and force (newton).