UNIZOR.COM - Physics4Teens - Electromagnetism - Magnetism and Electric C...

Notes to a video lecture on http://www.unizor.com



Parallel Currents - Problems 2



IMPORTANT NOTES



Recall the Lorentz force exerted by a magnetic field B (a vector) onto straight line electric current I (also a vector) of length L

F = I ·L⨯ B

The magnitude of this force can be expressed in terms of magnitudes of
the vectors of electric current and magnetic field, taking into
consideration an angle θ between them:

F = I·L·B·sin(θ)

In case electric current and magnetic field vectors are perpendicular to each other it looks as

F = I·L·B

The last formula will be used in this levture.



Also, as we know from previous lectures, the magnetic field force lines
around a long thin straight line wire with electric current I
running through it are circular in planes perpendicular to a wire and
centered at the points of the wire. Their direction is determined by a
corkscrew rule or the rule of the right hand.

On a distance R from the wire the vector of intensity of a magnetic field produced by this wire has a magnitude

B = μ₀·I/(2π·R)

where μ₀ is a constant permeability of vacuum.



The direction of this force vector at any point of space around a wire
corresponds to the direction of the circular magnetic field line going
through this point and is tangential to this magnetic line.



Problem 2A

Two ideally long and thin straight wires are parallel to each other and positioned at distance d from each other.

One wire carries an electric current of amperage I₁.

Another wire carries an electric current of amperage I₂ in the opposite direction.

Determine the magnitude of the repelling force between these two wires per unit of length of each.



Solution



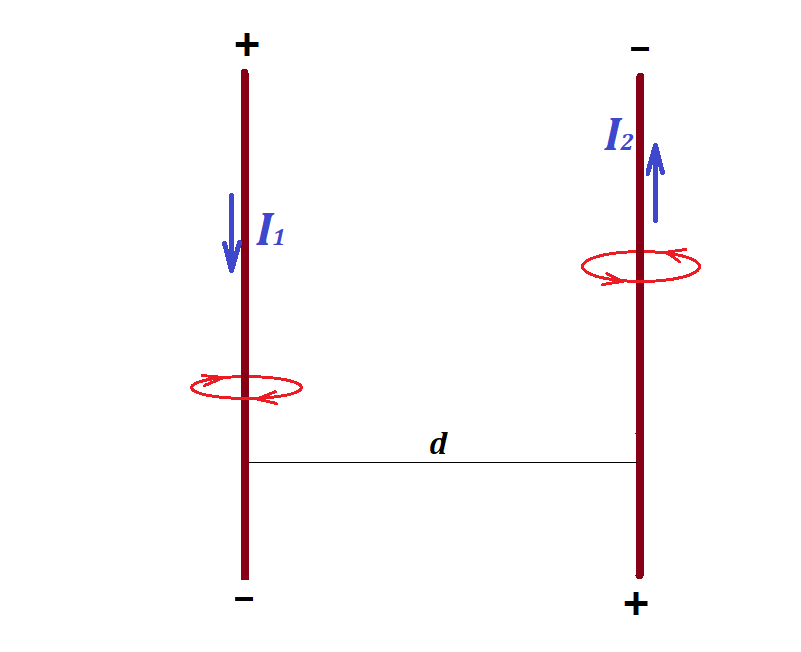
Consider the first wire as having an infinite length, while the second one to have a finite length L.

The magnetic field of the first wire at each point of the second wire can be considered as uniform, having a magnitude

B₁ = μ₀·I₁/(2π·d)

According to the formula for a force exerted by a uniform magnetic field
onto a wire with electric current that is perpendicular to the force of
magnetic field, the repelling Lorentz force exerted by the first wire
onto the second one is

F₁₂ = I₂·L·B₁ =

= μ₀·I₁·I₂·L /(2π·d)

If we calculate this force per unit of length of the second wire, the result is

F₁₂ = μ₀·I₁·I₂ /(2π·d)



Now consider a second wire as having an infinite length, while the first one to have a length L.

All previous results are applicable to this reverse logic, and we can
determine the magnitude of the repelling Lorentz force exerted by the
second wire per unit of length of the first

F₂₁ = μ₀·I₁·I₂ /(2π·d)

It's also a repelling force, so it's direction is opposite to F₁₂.



It's not coincidental that the forces F₁₂ and F₂₁ are equal in magnitude, since it corresponds to the Third Newton's Law.



Problem 2B

Two identical sufficiently long and thin straight wires of mass m per unit of length are horizontally hanging on threads of the same length L parallel to each other at the same height. The initial distance between them is d and they can swing on their corresponding threads parallel to themselves.

Initially there is no current in these wires and the threads holding these wires are in vertical position.

When we run electric current I through the first wire and the same in amperage electric current I through the second one in the opposite direction, the wires swing away from each other on their threads.

At equilibrium both threads made an angle φ with a vertical.

Determine the amperage I.



Solution

The following picture represents the view along the direction of wires
before and after the electric currents in both wires are turned on.


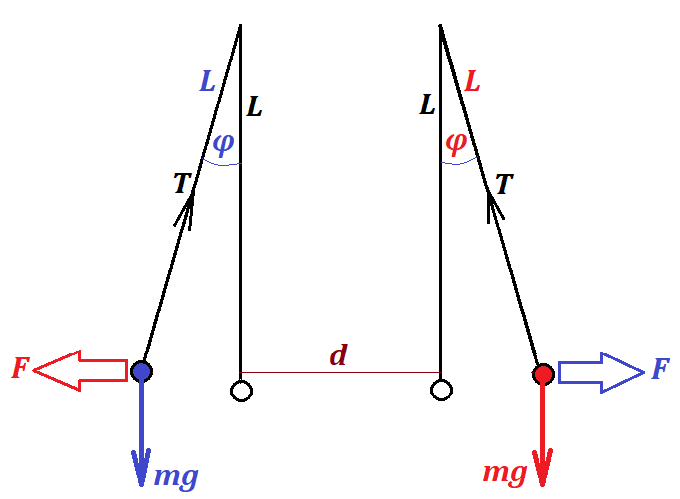
The wires are represented as circles. Before the electric current is
turned on the circles are white. When the electric current is on, the
circles are blue and red to represent the opposite directions of the
electric current in these wires.



Let T be the tension of a thread per unit length of a wire.

A vertical component of the thread tension per unit length of a wire T·cos(φ) balances the weight of the unit length of a wire m·g, which can be expressed as an equation

T·cos(φ) = m·g

from which we derive

T = m·g/cos(φ)



A horizontal component of the thread tension per unit length of a wire T·sin(φ) is supposed to balance the magnetic field repelling force, which has been calculated in the above Problem 2A as

F₁₂ = μ₀·I₁·I₂ /(2π·d)

except in our case

I₁ = I₂ = I

and, instead of the distance d we have to use D=d+2L·sin(φ) - the final distance between the wires at the point of equilibrium.

The result is

T·sin(φ) = μ₀·I² /(2π·D)

from which follows

I² = 2π·D·T·sin(φ)/μ₀ =

= 2π·D·m·g·sin(φ)/(μ₀·cos(φ)) =

= 2π·D·m·g·tan(φ)/μ₀

This gives the amperage of the current equal to

I = √2π·D·m·g·tan(φ)/μ₀

where D = d+2L·sin(φ)