Notes to a video lecture on http://www.unizor.com
Faraday's Law of
Electromagnetic Induction
Let's consider an experiment we described in a lecture about Lorentz
force exerted by a uniform magnetic field onto a wire with an electric
current running through it.
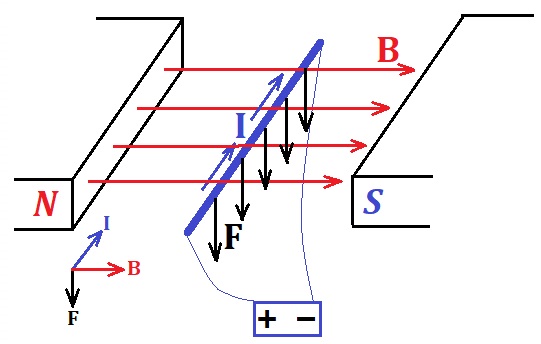
On this picture the density of magnetic field lines (red arrows)
represents the intensity of this field. If, for example, one line per
square centimeter of an area perpendicular to the direction of magnetic
field lines means the field of intensity 0.001T (i.e. 1/1000 of tesla), the density of 10 such lines per square centimeter signifies the intensity 0.01T (i.e. 1/100 of tesla).
In this lecture we will use an expression "the number of magnetic field
lines" in a context of a wire crossing them or sweeping across them. It
only means to demonstrate that the intensity of a magnetic field should
participate in our logic, formulas and calculations as a factor
proportional to a perpendicular to magnetic lines area, crossed or swept
across.
Recall that the Lorentz force exerted by a uniform magnetic field onto a
wire with an electric current running through it for any angle φ between the electric current in a wire and magnetic field lines equals to
F = I·L·B·sin(φ)
where
I is the amperage of an electric current running through a wire,
L is the length of a wire,
B is the strength of an external magnetic field
φ is the angle between the direction of the electric current and lines of an external magnetic field
Taking into consideration the direction of the Lorentz force
perpendicular to both vectors - electric current and lines of an
external uniform magnetic field, the above formula can be represented
using a vector product
F = I ·L⨯ B
In a simple configuration of the magnetic field and wire on a picture above φ=90° and the formula for a magnitude of a Lorentz force looks like
F = I·L·B
From the microscopic viewpoint the magnetic field exerts a Lorentz force
onto each electron moving inside the wire as a part of the electric
current. This force is perpendicular to both magnetic field lines and
the electric current in a wire and, consequently, causes the motion of
an entire wire.
If an electric current in a wire is produced by a charge q passing through a wire of length L during time t, thus making the electric current equal to I=q/t with the speed of moving V=L/t, the formula for Lorentz force acting on this charge becomes
F = I·L·B = (q/t)·(V·t)·B =
= q·V·B
The cause of the electric current in a wire and, therefore, motion of
electrons in one direction in the experiment above is some voltage or electromotive force (EMF) applied to wire's ends. So, the voltage or EMF at wire's ends causes the current in it and, consequently, its movement.
But what happens if we attempt to reverse the cause and effect and move the wire ourselves without any voltage applied to it?
Will the voltage be generated?
Consider a similar experiment, but no initial current running through a
wire. Instead, the wire is connected to an ammeter to measure the
intensity of the electric current running through it, thus making a
closed electric circuit.
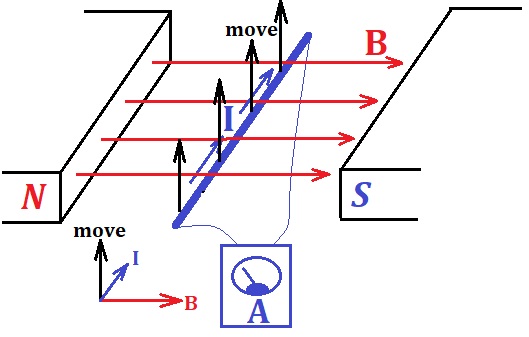
Let's move the wire in the upward direction as indicated on a picture.
The experiment shows that, while the wire is moving across the magnetic
field lines, there is an electric current in it.
Let's examine the reason why it happens.
There are positively charged nuclei of atoms relatively fixed in their
position by inter-atomic forces and there are electrons rotating around
these nuclei in each atom on different orbits. Usually, one or two
electrons from the outer orbits are relatively free to drift or exchange
their atom hosts. These "free" electrons are moving together with the
wire.
As we investigated the motion of charged particles in a magnetic field,
we came to a conclusion that there is a force acting on these charged
particles (electrons in our case) directed perpendicularly to their
trajectory - the Lorentz force.
Moving the wire across the magnetic field lines (upwards on a picture
above) results in the Lorentz force to act on "free" electrons, which
causes electrons to move in the direction of the Lorentz force
perpendicularly to their trajectory, while still being inside a wire.
So, they will move to one side of a wire, generating the difference in
charges on the wire's ends, that is generating the difference in
electric potentials or voltage or electromotive force (EMF).
If we have a loop with this wire being a part of it (like on a picture
with an ammeter in a loop), there will be an electric current in a wire.
As we see, the movement of a wire across the magnetic field lines generates a difference in electric potentials or an electromotive force (EMF) and, if there is a closed loop, an electric current in a wire. This is called electromagnetic induction.
Let's quantify the voltage (or electromotive power - EMF)
generated by a straight line wire moving in a uniform magnetic field
parallel to itself in a plane perpendicular to magnetic field lines.
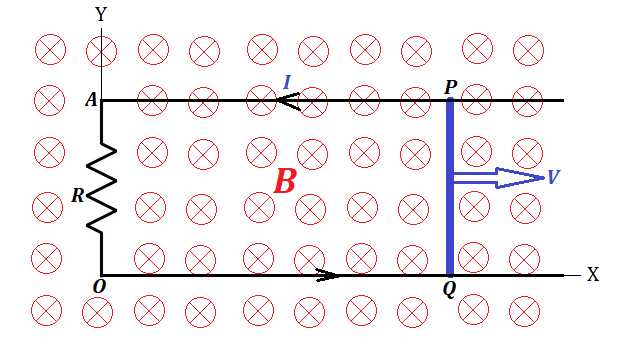
In a setup presented on the above picture the straight line wire PQ is moving parallel to itself and parallel to Y-axis along the rails AP and OQ stretched parallel to X-axis and connected by a resistor R, making a closed circuit with a wire PQ being a part of it.
The uniform magnetic field of intensity B is directed along the Z-axis perpendicularly to XY-plane in a direction of viewing the picture.
"Free" electrons, carried by a wire's motion along X-axis, experience
the Lorentz force directed perpendicularly to their movement inside a
wire, that is they will move to one end of a wire. The Lorentz force
acting on each such electron equals to (see Problem 1c in "Magnetic Field" topic of this course)
FL = e·V·B
where
e is an electric charge of an electron that is able to "freely" move,
V is the speed a wire moving along the X-axis,
B is the intensity of the magnetic field.
As a result, the difference in electric potential (or EMF) is generated and an electric current I will start running in the closed circuit OAPQ.
So, Lorentz force on electrons moving with a wire along the X-axis
causes the electrons to move to one end of a wire, that causes the
electric current in the wire. The latter causes the force exerted by the
magnetic field onto a wire in the direction opposite to its movement.
Since we are moving the wire ourselves with constant speed V
towards the positive direction of X-axis, we have to exert work against
the force of magnetic field onto a wire directed in the negative
direction.
This force of magnetic field onto a wire directed in the negative direction equals, as we mentioned above, to
F = I·L·B
where L is the length of a wire PQ.
If during time t the wire moves by a distance S=V·t, the work we have to do against the force F equals to
W = F·S = I·L·B·V·t
To do this work during a time interval t, we have to exert a power
P = W/t = F·S = I·L·B·V
Energy does not disappear without a trace. In this case the energy we spend generated voltage (EMF) U at wire's ends and an electric current I in a closed circuit. It will be transformed into heat in the resistor R with a rate I·U.
Therefore, we can equate two powers - the one we exerted to move a wire and the one consumed by a resistor:
I·L·B·V = I·U
from which we obtain the amount of EMF generated by moving the wire
U = L·V·B
Let's examine the expression on the right.
The value L·V represents the rate of increase of the area of a circuit OAPQ per unit of time.
The product of the area and the intensity of the magnetic field with
magnetic field lines going through this area perpendicularly to it is
called magnetic flux Φ.
Since our magnetic field is uniform, an expression L·V·B represents the rate of increase of magnetic flux, which we can safely denote using the language of calculus as dΦ/dt.
In this language we can state that the electromotive force (EMF) generated by a moving wire - a part of a closed circuit - equals to a rate of increase of magnetic flux going through this closed circuit.
U = dΦ/dt.
This is the Faraday's Law of electromagnetic induction.


No comments:
Post a Comment