Monday, July 30, 2018
Unizor - Physics4Teens - Mechanics - Dynamics - Rockets and Gravitation
Notes to a video lecture on http://www.unizor.com
Rocket in Gravitational Field
In the previous lectures we examined the motion of a rocket with no
external forces (like gravity or drag) acting on it and came with the
Rocket Equation, stating that
IF
m(t) is the mass of a rocket (including propellant) at time t and
V(t) is its speed in some inertial reference frame
(related to stars, for example, and positioned in such a way that a
rocket moves along one axis in a positive direction) and
m(t+Δt) is the mass after time interval Δt, during which a rocket was throwing propellant with constant (relatively to a rocket) effective exhaust speed ve and
V(t+Δt) is its speed after time interval Δt in the same inertial reference frame
THEN
the maximum increment of the rocket's speed
ΔV=V(t+Δt)−V(t) during this interval of time Δt is
ΔV = −ve·ln[m(t)/m(t+Δt)]
The equation above should be interpreted as the vector equation.
If inertial frame of reference is directed in such a way that the rocket
moves along one axis in positive direction and the exhaust is directed
backwards relative to a rocket's movement, the ve is negative. The mass during this process decreases, so m(t) is greater than m(t+Δt) and the logarithm is positive. This results in the positive ΔV, that is a rocket accelerates.
If the exhaust is directed forward relative to a rocket's movement, the ve is positive, ΔV is negative and a rocket decelerates.
Now let's add gravity as an external force that acts on a rocket.
There are two cases:
(a) when a rocket is launched from a planet to an orbit, gravity acts
against its movement, thus requiring extra effort by an engine to
overcome the gravity;
(b) when a rocket returns back to a planet for soft landing, gravity
acts in the direction of its movement, but we have to decelerate a
rocket using propellant exhausted also in the same direction, so it also
requires extra effort by an engine.
So, no matter how rocket moves in the gravitational field, an engine
should work harder to either launch it to an orbit or to slow it down
for soft landing.
We will consider the launching from the Earth case only.
Let's follow the same logic as in case of a rocket moving in empty space
with no forces involved and add the effect of gravity in the equation
of conservation of momentum.
1. At moment t the momentum of an entire system of a rocket with its propellant was equal to m(t)·V(t).
2. During the next time interval dt the rocket has exhausted m(t)−m(t+dt)=−dm(t) of propellant with constant relatively to a rocket speed ve. Since a rocket moves in some inertial system with speed V(t) and propellant moves relatively to a rocket with constant speed ve, the speed of propellant in the inertial system equals to ve+V(t). This resulted in the momentum of exhausted propellant at moment t+dt to be −dm(t)·[ve+V(t)].
This equation should be interpreted in the vector form. When a rocket
accelerates, velocity vector of its movement and velocity vector of
exhausted propellant are opposite in their directions.
3. A rocket with remaining propellant at moment t+dt has mass m(t+dt)=m(t)+dm(t), velocity V(t+dt)=V(t)+dV(t) and momentum
[m(t)+dm(t)]·[V(t)+dV(t)]
4. When rocket leaves the planet, the force of gravity F=m(t)·g acts against its movement. During time dt it reduces the impulse of a rocket by
F·dt = m(t)·g·dt.
Now we are ready to apply the Law of Conservation of Momentum.
Item 1 above describes the momentum of the system at time t.
At the moment t+dt the momentum of the system is a combination of the momentum of the exhausted propellant during time dt
(see item 2 above) plus the momentum of the remaining rocket mass (see
item 3 above) plus impulse of the gravitational force (see item 4
above).
Equalizing these two momentums at time t and t+dt, according to the Law of Conservation of Momentum, we get the following equation:
m(t)·V(t) = −dm(t)·[ve+V(t)] + [m(t)+dm(t)]·[V(t)+dV(t)] + m(t)·g·dt.
We would like to express the dependency between rocket's speed and the
way it exhausts its propellant without mentioning the time parameter.
This can be done by using the following:
m'(t) = dm(t)/dt (by definition of the derivative and differential)
From this:
dt = dm(t)/m'(t)
The rocket equation above can be simplified. After this the equation looks like
0 = −ve·dm(t) + m(t)·dV(t) + dV(t)·dm(t) + m(t)·g·dt
Ignoring an infinitesimal of a higher order dV(t)·dm(t), the resulting equation looks like
m(t)·dV(t)+m(t)·g·dt=ve·dm(t)
Divide both parts by m(t) and take into consideration that dm(t)/m(t) = d[ln(m(t))]. Then the differential equation of a rocket in the gravitational field looks like
dV(t) + g·dt = ve·d[ln(m(t))]
Replacing dt with its equivalent dm(t)/m'(t), we obtain an equivalent equation
dV(t)+g·dm(t)/m'(t) = ve·dm(t)
Expression on the right is positive because
(a) m(t) is a decreasing function,
(b) ln(m(t)), therefore, is also a decreasing function,
(c) differential of a decreasing function d[ln(m(t))] is always negative,
(d) ve is negative since it is a vector
directed against the movement of a rocket, which we consider as moving
to a positive direction of a coordinate axis,
(e) product of two negative values is positive.
As is obvious from this equation, unless g·dt is less than ve·d[ln(m(t))], the rocket will not move from the launching pad.
We can simplify this launching condition, using the following:
d[ln(m(t))] = [m'(t)/m(t)]·dt
This allows to express this condition as
g is less than ve·[m'(t)/m(t)]
or
ve·m'(t) is greater than g·m(t)
Integrating the differential equation of a rocket in the gravitational field on the interval Δt of time from the beginning of engine's work tbeg to the end of this period tend, we obtain the equation for an increment of the rocket's speed during this interval:
V(tend)−V(tbeg)+g·(tend−tend)=
= ve·[ln(m(tend))−ln(m(tbeg))]=
= ve·ln[m(tend)/m(tbeg)]=
= −ve·ln[m(tbeg)/m(tend)]
That is,
ΔV(t) = −ve·ln[m(tbeg)/m(tend)] − g·(tend−tend)
The last equation does not take into consideration that the force of
gravity decreases with height. It's relatively precise only in the
beginning of the rocket's movement. Obviously, taking this factor into
consideration will complicate the calculations.
The next complication is the drag of the atmosphere, which is not that
important in theory, but for practical matters must be taken into
consideration.
Another important factor of launching is the planet's rotation. If we
launch a rocket to the East, the Earth's rotation helps to achieve
required speed.
All these and other complications make rocket science a rather involved theory.
Friday, July 27, 2018
Unizor - Physics4Teens - Mechanics - Dynamics - Rocket Calculations
Notes to a video lecture on http://www.unizor.com
Rocket Calculation 1
Let's use the rocket equation
ΔV = −ve·ln[m(tbeg)/m(tend)]
to calculate how much propellant must be taken by a rocket to reach an orbit.
Here ve is effective exhaust speed, m(tbeg) - mass of a rocket in the beginning of a time period during which a rocket's engine is working, m(tend) - mass of a rocket at the end of this period of acceleration or deceleration.
Recall that the minus sign in this equation signifies the vector
character of the movement: positive direction of the exhausted
propellant (that is, the same as the movement of the rocket) causes
negative increment in rocket's speed - deceleration, while the negative
direction of exhausted propellant (that is, opposite to the movement of a
rocket) causes increase in rocket's speed - acceleration.
Contemporary rocket engine can have a very high effective exhaust
velocity. The speed of about 4km/sec is mentioned in a few sources we
are familiar with. So, we can assume that
ve=4000m/sec.
An international Space Station's speed is about 7.8km/sec, as was calculated in one of the previous lectures on gravity.
Assuming that the initial speed of a rocket is zero, the increment of speed of a rocket must be
ΔV = 7800m/sec
From this follows that
ln[m(tbeg)/m(tend)] =
= 7800/4000 = 1.95
Therefore,
m(tbeg)/m(tend) ≅ 7
So, the mass of a rocket at start is 7 times greater than its mass at
the end of its acceleration. For example, to launch 1,000 kg of useful
equipment and/or passengers to an International Space Station we will
need 6,000 kg of fuel.
Rocket Calculation 2
We still assume that
ve=4000m/sec.
A rocket that goes far from Earth needs about 11.2km/sec speed to escape Earth gravity.
Assuming that the initial speed of a rocket is zero, the increment of speed of a rocket must be
ΔV = 11200m/sec
From this follows that
ln[m(tbeg)/m(tend)] =
= 11200/4000 = 2.8
Therefore,
m(tbeg)/m(tend) ≅ 16
So, the mass of a rocket, that is supposed to leave the Earth's gravity,
at start is 16 times greater than its mass at the end of its
acceleration. For example, to launch 1,000 kg of useful equipment and/or
passengers to Mars we will need 15,000 kg of fuel.
Wednesday, July 25, 2018
Unizor - Physics4Teens - Mechanics - Dynamics - Rocket Equation
Notes to a video lecture on http://www.unizor.com
Ideal Rocket Equation
(Tsiolkovsky's Equation)
The most important difference between the motion of a rocket and motions
analyzed before in this course is that the rocket propels itself by
throwing back part of its own mass (propellant), thus becoming lighter.
Its mass is variable. Before, in most cases, we were dealing with motion
of objects of some specific mass, not changing during the movement.
In this lecture we will analyze the motion of an ideal rocket that
throws back propellant with constant (relatively to the rocket) speed.
The formula that will be derived was suggested by Russian mathematician
K.E.Tsiolkovsky and is historically named after him, though he was not
the first to derive it.
In particular, we will analyze the dependency between loss of the total
mass of a rocket, throwing propellant backward in the absence of any
external forces, and its gain in speed caused by this process.
The final formula we will derive states that
IF
m(t) is the mass of a rocket (including propellant) at time t and
V(t) is its speed in some inertial reference frame
(related to stars, for example, and positioned in such a way that a
rocket moves along one axis in a positive direction) and
m(t+Δt) is the mass after time interval Δt, during which a rocket was throwing propellant with constant (relatively to a rocket) effective exhaust speed ve and
V(t+Δt) is its speed after time interval Δt in the same inertial reference frame
THEN
the maximum increment of the rocket's speed
ΔV=V(t+Δt)−V(t) during this interval of time Δt is
ΔV = −ve·ln[m(t)/m(t+Δt)]
The equation above should be interpreted as the vector equation.
If inertial frame of reference is directed in such a way that the rocket
moves along one axis in positive direction and the exhaust is directed
backwards relative to a rocket's movement, the ve is negative. The mass during this process decreases, so m(t) is greater than m(t+Δt) and the logarithm is positive. This results in the positive ΔV, that is a rocket accelerates.
If the exhaust is directed forward relative to a rocket's movement, the ve is positive, ΔV is negative and a rocket decelerates.
Here is how to derive this formula.
First of all, let's recall that in the absence of external forces the
combined momentum of motion of a system of objects is constant.
This is the Law of Conservation of Momentum.
Let's apply this law to our situation.
Assume, we are comparing the momentum of the system at times t and infinitesimally incremented t+dt.
1. At moment t the momentum of an entire system of a rocket with its propellant was equal to m(t)·V(t).
2. During the next time interval dt the rocket has exhausted m(t)−m(t+dt)=−dm(t) of propellant with constant relatively to a rocket speed ve. Since a rocket moves in some inertial system with speed V(t) and propellant moves relatively to a rocket with constant speed ve, the speed of propellant in the inertial system equals to ve+V(t). This resulted in the momentum of exhausted propellant at moment t+dt to be −dm(t)·[ve+V(t)].
This equation should be interpreted in the vector form. When a rocket
accelerates, velocity vector of its movement and velocity vector of
exhausted propellant are opposite in their directions.
3. A rocket with remaining propellant at moment t+dt has mass m(t+dt)=m(t)+dm(t), velocity V(t+dt)=V(t)+dV(t) and momentum
[m(t)+dm(t)]·[V(t)+dV(t)]
Now we are ready to apply the Law of Conservation of Momentum.
Item 1 above describes the momentum of the system at time t.
At the moment t+dt the momentum of the system is a combination of the momentum of the exhausted propellant during time dt (see item 2 above) plus the momentum of the remaining rocket mass (see item 3 above).
Equalizing these two momentums at time t and t+dt, which is the consequence of the Law of Conservation of Momentum, we get the following equation:
m(t)·V(t) =
= −dm(t)·[ve+V(t)] +
+ [m(t)+dm(t)]·[V(t)+dV(t)]
This can be simplified. After this the equation looks like
0 = −ve·dm(t) + m(t)·dV(t) +
+ dV(t)·dm(t)
The last member in this equation dV(t)·dm(t) is an infinitesimal of the higher order that we can remove from this equation, and the resulting equation looks like
m(t)·dV(t) = ve·dm(t)
Divide both parts by m(t) and take into consideration that dm(t)/m(t) = d[ln(m(t))]. Then our equation looks like
dV(t) = ve·d[ln(m(t))]
Integrating this on the interval Δt of time from the beginning of engine's work tbeg to the end of this period tend, we obtain the equation for an increment of the rocket's speed during this interval:
V(tend) − V(tbeg) = ΔV(t) =
= ve·[ln(m(tend))−ln(m(tbeg))]=
= ve·ln[m(tend)/m(tbeg)]=
= −ve·ln[m(tbeg)/m(tend)]
That is,
ΔV(t) =−ve·ln[m(tbeg)/m(tend)]
So, the increment of a rocket's speed during a period of Δt=tend−tbeg,
when its engine works, exhausting the propellant, equals to a product
of the speed of exhausted propellant times a logarithm of a ratio of the
rocket's mass at the beginning of this period to its mass at the end of
it.
The minus in front of a formula is very important. This is a vector
equation and, if the exhaust is directed back relatively to rocket's
movement (that is, ve is negative), the
increment of a rocket's speed is positive, a rocket accelerates; if,
however, the exhaust is directed towards a tocket movement (that is, ve is positive), the increment of a rocket's speed is negative, a rocket slows down.
The formula above is the Tsiolkovsky's formula and is called the "ideal rocket equation".
Tuesday, July 17, 2018
Unizor - Physics4Teens - Mechanics - Dynamics - Spring Oscillation
Notes to a video lecture on http://www.unizor.com
Spring
Consider a point-object of mass m, hanging vertically at
the lower end of a weightless spring, that is fixed at the upper end.
Under the weight of this object a spring will stretch a little from its
neutral position.
The Hook's Law for a spring, which will be used to solve this problem, involves a spring's elasticity constant k, that we assume is given.
Let's stretch this spring even more, so that the distance between an object at its bottom and a spring's neutral level is L and let it go without any push.
Our task is to analyze the oscillation of the object as a function x(t) of its vertical deviation from a spring's neutral position.
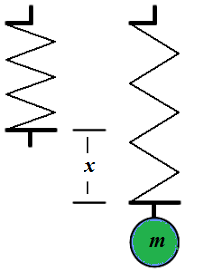
The obvious initial conditions of the motion of our object are:
x(0) = L
x'(0) = 0
There are two forces acting on our object:
(a) its weight W, directed vertically down and equal in magnitude to m·g, where g is the acceleration of free falling
W = m·g
(b) the spring's elasticity force F, equal in magnitude to a coefficient of elasticity k
multiplied by a displacement of the spring's bottom end from a neutral
level; the direction of this force is always against the direction of
the displacement
F = −k·x(t)
The resultant of the superposition of these two forces can be equated to
mass times acceleration of the object, according to the Newton's Second
Law:
m·g − k·x(t) = m·x"(t)
This is the differential equation that defines the movement of our object.
We don't have to resort to modifying this differential equation with an
approximate one to be able to solve it. It is fully solvable and the
general solution of this linear differential equation of the second
order is
x(t) = C1·cos(t·√k/m) +
+ C2·sin(t·√k/m) + m·g/k
Now we can apply the initial conditions to determine constants C1 and C2.
Since x(0) = L,
C1 = L − m·g/k
Since x'(0) = 0,
C2 = 0
This produces the following expression for x(t):
x(t) = (L − m·g/k)·cos(t·√k/m) +
+ m·g/k
Interestingly, if
L − m·g/k = 0 or L·k = m·g
(which means that the weight W=m·g is balanced by the force of spring's elasticity F=−L·k in its initial position with our object at its end) then there are no oscillations, and the object will remain at distance L=m·g/k from a spring's neutral position.
If there are oscillations, their period is
T = 2π√m/k
Monday, July 16, 2018
Unizor - Physics4Teens - Mechanics - Dynamics - Pendulum
Notes to a video lecture on http://www.unizor.com
Pendulum
We will analyze the ideal (mathematical) pendulum, which is a mechanical device placed near the surface of a planet with free fall acceleration g (to have the gravitational force acting on it) that consists of a point-object of certain mass m, hanging on a weightless non-stretchable thread of length L, fixed at the other end, so that the hanging on it object has freedom of motion.
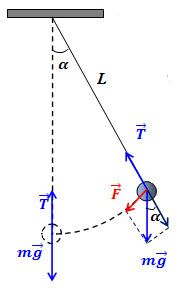
Assume that at time t=0 we have tilted a point-object at the end of thread of a pendulum by an angle α0 from vertical. Then we let it go without any push.
Our task is to determine, how an angle of deviation of this pendulum
from a vertical changes with time, that is we have to find the function α(t).
We can say now that initial (at time t=0) position of a pendulum is
α(0) = α0
Considering that linear displacement d along a circular trajectory of a radius L and its angular displacement α are related by a formula
d = L·α,
the initial condition of not pushing a pendulum, which means "no initial
linear velocity along its trajectory", means that the first derivative
of angular displacement is zero:
α'(0) = 0
Having these initial conditions, we'll determine the equation that function α(t) must satisfy, using the Newton's Second Law.
The force of gravity P=mg can be represented as a sum of two forces:
- a force along a pendulum's thread, that is completely balanced by a
thread's reaction, which results in constant distance of a point-object
at the end of a thread from its other (fixed) end; this force constrains
the movement of a point-object within a circular trajectory and is
equal to
mg·cos(α(t))
- a force tangential to a circular trajectory of a point-object at the
end of a thread; this force is the source of movement along a trajectory
and is equal to
F = −mg·sin(α(t))
(negative sign is used because the force is always directed in an opposite direction to the movement)
The force tangential to a circular trajectory is the one that
accelerates our point-object. Since the displacement along a circular
trajectory is, as we indicated, d=L·α, the linear acceleration along a trajectory is equal to a second derivative of this expression by time
a = L·α"(t)
The Newton's second law states that
m·a = F
which results in the following differential equation for function α(t):
m·L·α"(t) = −m·g·sin(α(t))
The good news is that we can reduce this by mass m, which
means that the oscillation of a pendulum does not depend on a mass of a
point-object at its end, but only on the length of a thread L and acceleration of free falling g.
So, we deal with an equation
L·α"(t) = −g·sin(α(t)) or
α"(t) = −(g/L)·sin(α(t))
Another good news is that this is a differential equation of the second
order (highest derivative is the second one) and we have two initial
conditions for a function α(t) at t=0 and for its first derivative α'(t) at t=0.
This fully identifies the function α(t).
Unfortunately, the bad news is that this differential equation cannot be
solved in terms of simple algebraic functions, but only numerically
tabulated using computer.
But physicists, in their endless quest for simple solutions to
complicated problems of the Universe, have decided that within certain
boundaries they can simplify the above equation to approximate its
solution, using simple algebraic functions.
This simplification is based on the fact that, when an angle is
relatively close to zero, its sine is not much different from the value
of an angle itself (in radians). This is based on a famous limit
limx→0[sin(x)/x] = 1
So, for relatively small angles around a vertical, the oscillations of a
pendulum can be approximately expressed by an equation obtained by
replacing sin(α(t)) with simple α(t).
This produces the following equation:
α"(t) = −(g/L)·α(t)
This is a simple linear differential equation with general solution
α(t) = C1·cos(√g/L·t) + C2·sin(√g/L·t)
where C1 and C2 are some constants.
To determine the values of these constants, we will use the initial conditions:
α(0) = α0 and α'(0) = 0
This results in the following:
C1·cos(0) + C2·sin(0) = α0
and
−C1·sin(0) + C2·cos(0) = 0
from which follows that
C1 = α0
and
C2 = 0
Solution to our problem, therefore, is
α(t) = α0·cos(√g/L·t)
This solution represents harmonic oscillation with an amplitude
A = α0
and period
T = 2π /√g/L = 2π·√L/g
The above approximate solution satisfies to a certain degree
physicists and is accepted as the one describing relatively small
harmonic oscillations of pendulum around a vertical.
Oscillations on a bigger scale (say, with initial angle of deviation
around 45° or so) do not conform to this formula and are not harmonic.
Friday, July 13, 2018
Unizor - Physics4Teens - Mechanics - Dynamics - Weight
Notes to a video lecture on http://www.unizor.com
Weight
Weight of an object, by definition, is the force of gravity a
planet attracts this object with. Usually, the word "weight" implies the
magnitude of this force; its direction is, obviously, always towards a
center of a planet.
So, weight is not a characteristic of an object itself, it's a
characteristic of an object relative to a planet. In most cases, this
planet is our Earth, though we sometimes say, for example, that a
particular object weighs on the Earth 6 times more than on the Moon.
This only means that the force of gravity on the surface of the Moon is 6
times weaker than on the surface of the Earth.
Do we feel weight as the force of gravity?
Not quite. What we can feel is pressure (reaction force) from the surface we stand on, that equalizes gravitational force to hold us at fixed position on a floor or on a ground.
If there is no support (like for a person jumping with a parachute from
an airplane before a parachute is open, if we ignore the air
resistance), we don't feel weight, we are weightless. We have different
senses, but not a sense of gravity.
So, feeling weightless is not really an absence of gravity, it's absence
of a reaction force that balances the gravity (equal in magnitude and
opposite in direction) and holds us fixed relatively to a planet.
This reaction force is not just against our feet, when we stand on the
floor, it's everywhere inside our body as well, since the body maintains
its shape. We feel this pressure of a reaction force everywhere inside.
That's why it's very difficult to emulate the gravity with some special
equipment on a spaceship.
People on a spaceship with non-working engines flying around the Earth
on an orbit feel weightless, because they are constantly falling towards
the Earth together with a spaceship (no support!) from the straight
line trajectory tangential to an orbit; planet attracts them with
gravitational force, and only because of the speed, they maintain
constant distance from the planet.
Since weight is a force, it is measured in units of force, like newtons in SI.
The weight of an object of mass m on a surface of a planet of mass M and radius R is, as we know,
W = G·M·m /R²
where G is a universal gravitational constant,
G = 6.674·10−11 N·m²/kg²
Since we are talking about weight as a force, which is a subject to the
Newton's Second Law, we can determine the acceleration this force causes
to an object of mass m, if acts alone:
a = W/m = G·M /R²
Notice that on the surface of Earth this acceleration is constant since
all components of this expression (gravitational constant G,
mass of Earth M and its radius R) are constants.
So, we can calculate this constant once and for all and, knowing the mass of an object m,
we can determine its weight by multiplying it by this constant, which
is, as we determined in the previous lecture, an acceleration of free
fall, which on the surface of Earth is traditionally symbolized by
letter g:
g = G·M /R²
The value of this constant is, approximately, 9.8 m/sec².
But, to be precise, it's not the same at different points on the Earth
because the shape of the Earth is not exactly a sphere and its mass is
not uniformly distributed within its volume.
Moreover, it obviously changes with height (getting smaller) since the higher elevation is equivalent to a greater radius R (distance to a center of the Earth) of an object.
Now we can say that for an object of mass m the weight on the surface of the Earth is W=m·g=9.8·m. If mass m is measured in kilograms, this weight is measured in newtons.
Analogous calculation for other planets, based on their mass and radius, show the following values of free falling acceleration:
on Sun - 274.1 m/sec²
(objects are 28 times heavier on Sun than on Earth),
on Jupiter - 25.93 m/sec²
(objects are about 2.6 times heavier on Jupiter than on Earth),
on Moon - 1.625 m/sec²
(objects are about 6 times lighter on Moon than on Earth).
Historically, the weight is rarely measured in newtons. More customary units are:
1 pound (abbreviated lb) equals to 4.44822 newtons - the weight of an object of mass 0.454 kg on Earth;
1 kilogram-force (usually, simply called 1 kilogram, skipping "-force", and abbreviated kgf, but plain kg can also be used, when implication to weight is obvious) equals to weight of an object of mass of 1 kg on Earth, that is 9.8 newtons;
and others.
Tuesday, July 10, 2018
Unizor - Physics4Teens - Mechanics - Dynamics - Free Falling
Notes to a video lecture on http://www.unizor.com
Free Falling
Free falling is a movement of an object on a surface of a planet
relative to this surface, when the only force acting on this object is
the gravitational force of a planet.
Our task is to describe this movement in mechanical terms of force, mass and acceleration.
In this task we will assume that
(a) an object in question is a point-object of mass m,
(b) a planet has a spherical form and its mass M is uniformly distributed within its volume,
(c) a planet has a radius R,
(d) [an important assumption that can be justified by complex
calculations] we can model the combined forces of gravitation between
all microscopic particles inside a planet and our object in question as a
gravitational force of a point-object of mass M positioned at the center of a planet.
In this case the one and only force of attraction acting on an object
and directed towards the center of a planet can be expressed using the
Law of Gravitation as follows:
F = G·M·m /R²
where G is a gravitational constant,
G = 6.674·10−11 N·m²/kg²
Knowing the force of gravity F and mass of an object m, we can determine the acceleration using the Newton's Second Law:
a = F/m = G·M /R²
Notice that this acceleration does not depend on m - mass of an object, which means that all objects fall on the surface of a planet with the same acceleration.
An interesting aspect of this formula is that we can imagine how to
measure an acceleration (easy) and radius of a planet (more difficult,
but possible), while we have no idea how to measure the mass of a
planet.
So, this formula is used exactly for this purpose - to determine the mass of a planet, resolving the formula above for M:
M = a·R² /G
Experiments show that on the surface of our planet Earth the acceleration caused by gravitational force is approximately 9.8 m/sec².
The radius of Earth is approximately 6.4·106 m.
From this we can calculate the mass of Earth (in kilograms - units of mass in SI):
M≅9.8· 6.4²·1012/(6.674·10−11)
The result of this calculation is
M ≅ 6·1024 kg
Let's solve a different problem now. We'd like to launch a satellite
around the Earth that circulates around the planet at height H. What linear speed should a satellite have to stay on a circular orbit?
We know from Kinematics that an object rotating along a circular trajectory of radius r and angular speed ω has acceleration a=r·ω².
In terms of linear speed V=r·ω along an orbit this formula looks like
a = V²/r
Since the radius of an orbit is the radius of Earth R plus the height above its surface H, we should replace r in this formula with R+H.
The force of gravity is the only force acting on a satellite and the
only source of its acceleration towards the Earth, so the acceleration
above must be equal to acceleration of a free fall of a satellite. Here
we will take into consideration already known mass of Earth and use
distance from the center of the Earth to satellite as R+H, where R is the radius of Earth and H is a height above the Earth's surface.
The acceleration of a free fall to Earth at height H above the surface, using its radius R and already calculated mass of Earth M, is:
a = G·M/(R+H)²
Therefore, equating the acceleration of free fall to acceleration of an
object rotating along a circular orbit, we come to the following
equation:
V²/(R+H) = G·M/(R+H)²
from which we derive the value of required linear speed V:
V = √G·M/(R+H)
For example, International Space Station rotates around our planet on a height of about 400 kilometers (4·105 meters).
That means that, to stay on an orbit, it should have linear speed of
V ≅ 0.78·104 m/sec
which is about 28,000 km/hour.
Monday, July 9, 2018
Unizor - Physics4Teens - Mechanics - Dynamics - Gravity
Notes to a video lecture on http://www.unizor.com
Gravity
We all know a lot about gravity, weight, weightlessness, rockets flying on orbits calculated based on the laws of gravity etc.
But what is gravity?
A short answer is: we don't know. It's like most of us can use a smart
phone and Global Positioning System (GPS), but don't know how and why it
works. It just works, we know what to do to effectively use it, but
have no idea about the real mechanism that allows us to use it.
Obviously, designers and engineers who created these technological
marvels know, but most of people don't.
With gravity it's similar. We know it exists, we can use it, we feel it,
but we don't know the underlying reason why it is what it is.
To be more precise, physicists have certain ideas about the source of
gravity, but they are rather vague, on the level of hypothesis.
Therefore, we skip this foundational discussion about why gravity
exists, what is an underlying mechanism of its work. We will just use it
as we use GPS without getting much deeper.
To use a computer game, we just have to know its rules and controls, we don't have to know what software is inside.
To use gravity, it's not necessary to know its underlying mechanism, we
just need to know its properties, and that's the subject of this
lecture.
The first fundamental property of gravity is that all objects we deal
with attract other objects. This effect of attraction is called gravity.
Attraction is a force.
Since we usually model physical objects as points, this force is
directed along the line connecting these point-objects and pushes them
towards each other.
It is also important to note that the Newton's Third Law says that the force point-object B attracts point-object A is paired with the same in magnitude and opposite in direction force point-object A attracts point-object B.
In more complicated cases of objects that cannot be considered as
points, we can assume that every tiny peace of each object, which can be
modeled as a point-object, is attracted to every other tiny peace. Then
some process of integration of all these forces might be used to
determine the resultant forces. But we will rarely deal with this type
of gravitation, most of cases we will consider will involve
point-objects.
Forces change the velocity. Therefore, gravity, which is the force
observed for any type of object, causes change of motion of objects. If
there is only one point-object in the Universe, it will maintain its
inertial motion along a straight line with constant velocity. As soon as
another object appears somewhere, the force of gravity will cause a
change in the inertial movement of the first object.
Our next question is: how exactly forces of gravity change the motion of objects?
Different objects attract differently.
Consider some probe object A in inertial motion along a straight
line with constant velocity. For example, it flies in our
three-dimensional space along the X-axis in positive direction, going
through point of origin of coordinates
Let's measure the degree of the change of its motion, when at the later moment of time t=1 another object B appears at the origin of coordinates
will decelerate. Measuring this deceleration and knowing the mass of
objects involved, we can measure the force of attraction between objects
A and B using the Newton's Second Law.
Our observations show that different objects B will cause different decelerations of probe object A and the same object B causes different decelerations of probe object A at different distances between them. We conclude then that gravitational force of attraction between objects A and B depends on gravitational properties of objects themselves and on distance between them.
Our purpose is to analyze what is the gravitational property of any
object, how to measure it and how the force of gravity depends on it and
the distance between objects.
The situation with distance is easy.
Experiments with the same objects showed that the gravitational force of
attraction between them weakens with distance in inverse proportion to a
square of this distance. In other words, if the distance between any
two objects A and B doubles, the gravitational force of attraction weakens by a factor of 4.
So, it is sufficient to establish the gravitational force between two
objects at a unit length (say, 1 meter), after which the gravitational
force between these objects at any distance D will be that force at a unit distance divided by a factor D2.
Let's discuss now the gravitational property of an object, its ability to attract other objects, which in Physics is called gravitational mass of an object.
An experimental fact is that two identical objects, B1 and B2 combined together, attract twice as strongly as only one of them, say B1, providing they attract the same probe object A, and the relative position of participating objects is the same.
That means that gravitational mass is additive and the gravitational force is proportional to gravitational mass.
Let's choose one particular probe object A and assign it a gravitational mass of a unit and another identical object B. Since they are identical, the gravitational mass of object B is also a unit.
Then, comparing the attraction between this unit probe object A and identical unit object B at the unit distance with the attraction of any other object C to the same unit probe object A on the same unit distance, we can assign a gravitational mass to that other object C. Since gravitational mass is additive, the stronger the gravitational force of object C - the proportionally greater is its gravitational mass relative to a unit object B.
Notice, that additive property of gravitational mass is similar to a property of inertial mass, which is also additive. This is precisely the reason why both properties are call mass.
The analogy goes further. Another experimental fact is that two different objects of the same inertial mass have exactly the same gravitational mass,
that is they attract equal probe objects on equal distance equally.
From this follows that the quantitative difference between inertial mass and gravitational mass is just in units of measurement.
Based on this, it was decided to measure the gravitational mass in exactly the same units as inertial mass and, by definition, say that an object of 1 kilogram of inertial mass has 1 kilogram of gravitational mass, which, quantitatively, fully characterizes the gravitational properties of an object.
When we talk about gravity, 1 kilogram is a measure of gravitational attraction of an object, its gravitational mass. When we discuss inertia, motion, force, 1 kilogram is a measure of an object's inertial mass.
Let's derive the formula that expresses the force of gravity between two
point-objects in terms of their gravitational masses and distance
between them.
We already know that the force of gravity is proportional to a
gravitational mass, but, since we always deal with two point-objects,
the force must be proportional to a gravitational mass of each of them,
that is it is proportional to their product.
We also know that the force of gravity is inversely proportional to a square of a distance between objects.
These two factors lead to the following formula for the force F of gravity between two point-objects with gravitational (and inertial, as we defined) masses M1 and M2 at distance r between them:
F = G·M1·M2 /r²
where G - a constant of proportionality, since the units
of force (N - newtons) have been defined already, and we want to measure
the gravitational force in the same units as any other force.
This formula was presented by Sir Isaac Newton in 17th century, though other scientists, like Robert Hooke claimed it as well.
Physicists call this formula the Newton's Law of Universal Gravitation.
To determine the constant G in this formula, all we need
to do is to place two objects of inertial (and gravitational, as we
defined) mass of 1 kilogram each at the distance of 1 meter and measure
the force of gravity between them by measuring an acceleration they
develop as a result of gravitational force. This force (in newtons) will
be quantitatively equal to a gravitational constant G.
This measurement shows a very weak force, and the gravitational constant equals to
G = 6.674·10−11 N·m²/kg²
Finally, let's attempt to explain the phenomenon of weakening of the
gravitational force inversely proportional to a square of a distance
from the gravitating object.
This is not really a theoretical proof, but a reasonable explanation of this fact.
Assume that the source of gravitational force around an object is
something similar to tentacles of an octopus with objects of larger
gravitational mass corresponding to greater number of tentacles. The
gravitational grip, presumably. depends on the density of tentacles per
unit of covered area.
To propel gravity on a longer distance the tentacles should be longer, while their quantity remains the same.
Now, the longer these tentacles - the more is the area they have to spread around. This area for tentacle of the length r is a surface of the sphere of this radius, that is 4r².
So, area these tentacles are supposed to cover is increasing as a
square of their length, which causes a gravitational grip to be weaker
in exactly the same proportion.
Subscribe to:
Posts (Atom)

