Unizor - Physics4Teens - Mechanics - Dynamics - Pendulum

Notes to a video lecture on http://www.unizor.com



Pendulum



We will analyze the ideal (mathematical) pendulum, which is a mechanical device placed near the surface of a planet with free fall acceleration g (to have the gravitational force acting on it) that consists of a point-object of certain mass m, hanging on a weightless non-stretchable thread of length L, fixed at the other end, so that the hanging on it object has freedom of motion.





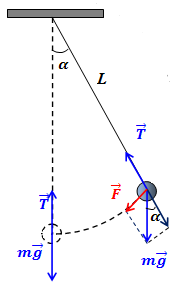
Assume that at time t=0 we have tilted a point-object at the end of thread of a pendulum by an angle α₀ from vertical. Then we let it go without any push.

Our task is to determine, how an angle of deviation of this pendulum
from a vertical changes with time, that is we have to find the function α(t).



We can say now that initial (at time t=0) position of a pendulum is

α(0) = α₀

Considering that linear displacement d along a circular trajectory of a radius L and its angular displacement α are related by a formula

d = L·α,

the initial condition of not pushing a pendulum, which means "no initial
linear velocity along its trajectory", means that the first derivative
of angular displacement is zero:

α'(0) = 0



Having these initial conditions, we'll determine the equation that function α(t) must satisfy, using the Newton's Second Law.

The force of gravity P=mg can be represented as a sum of two forces:

- a force along a pendulum's thread, that is completely balanced by a
thread's reaction, which results in constant distance of a point-object
at the end of a thread from its other (fixed) end; this force constrains
the movement of a point-object within a circular trajectory and is
equal to

mg·cos(α(t))

- a force tangential to a circular trajectory of a point-object at the
end of a thread; this force is the source of movement along a trajectory
and is equal to

F = −mg·sin(α(t))

(negative sign is used because the force is always directed in an opposite direction to the movement)



The force tangential to a circular trajectory is the one that
accelerates our point-object. Since the displacement along a circular
trajectory is, as we indicated, d=L·α, the linear acceleration along a trajectory is equal to a second derivative of this expression by time

a = L·α"(t)

The Newton's second law states that

m·a = F

which results in the following differential equation for function α(t):

m·L·α"(t) = −m·g·sin(α(t))



The good news is that we can reduce this by mass m, which
means that the oscillation of a pendulum does not depend on a mass of a
point-object at its end, but only on the length of a thread L and acceleration of free falling g.

So, we deal with an equation

L·α"(t) = −g·sin(α(t)) or

α"(t) = −(g/L)·sin(α(t))



Another good news is that this is a differential equation of the second
order (highest derivative is the second one) and we have two initial
conditions for a function α(t) at t=0 and for its first derivative α'(t) at t=0.

This fully identifies the function α(t).



Unfortunately, the bad news is that this differential equation cannot be
solved in terms of simple algebraic functions, but only numerically
tabulated using computer.



But physicists, in their endless quest for simple solutions to
complicated problems of the Universe, have decided that within certain
boundaries they can simplify the above equation to approximate its
solution, using simple algebraic functions.

This simplification is based on the fact that, when an angle is
relatively close to zero, its sine is not much different from the value
of an angle itself (in radians). This is based on a famous limit

lim_x→0[sin(x)/x] = 1

So, for relatively small angles around a vertical, the oscillations of a
pendulum can be approximately expressed by an equation obtained by
replacing sin(α(t)) with simple α(t).



This produces the following equation:

α"(t) = −(g/L)·α(t)

This is a simple linear differential equation with general solution

α(t) = C₁·cos(√g/L·t) + C₂·sin(√g/L·t)

where C₁ and C₂ are some constants.

To determine the values of these constants, we will use the initial conditions:

α(0) = α₀ and α'(0) = 0

This results in the following:

C₁·cos(0) + C₂·sin(0) = α₀

and

−C₁·sin(0) + C₂·cos(0) = 0

from which follows that

C₁ = α₀

and

C₂ = 0



Solution to our problem, therefore, is

α(t) = α₀·cos(√g/L·t)



This solution represents harmonic oscillation with an amplitude

A = α₀

and period

T = 2π /√g/L = 2π·√L/g



The above approximate solution satisfies to a certain degree
physicists and is accepted as the one describing relatively small
harmonic oscillations of pendulum around a vertical.

Oscillations on a bigger scale (say, with initial angle of deviation
around 45° or so) do not conform to this formula and are not harmonic.