Unizor - Physics4Teens - Mechanics - Dynamics - Spring Oscillation

Notes to a video lecture on http://www.unizor.com



Spring



Consider a point-object of mass m, hanging vertically at
the lower end of a weightless spring, that is fixed at the upper end.
Under the weight of this object a spring will stretch a little from its
neutral position.



The Hook's Law for a spring, which will be used to solve this problem, involves a spring's elasticity constant k, that we assume is given.



Let's stretch this spring even more, so that the distance between an object at its bottom and a spring's neutral level is L and let it go without any push.



Our task is to analyze the oscillation of the object as a function x(t) of its vertical deviation from a spring's neutral position.







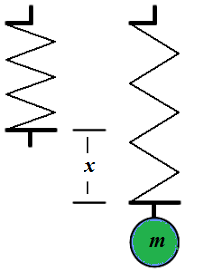
The obvious initial conditions of the motion of our object are:

x(0) = L

x'(0) = 0



There are two forces acting on our object:

(a) its weight W, directed vertically down and equal in magnitude to m·g, where g is the acceleration of free falling

W = m·g

(b) the spring's elasticity force F, equal in magnitude to a coefficient of elasticity k
multiplied by a displacement of the spring's bottom end from a neutral
level; the direction of this force is always against the direction of
the displacement

F = −k·x(t)



The resultant of the superposition of these two forces can be equated to
mass times acceleration of the object, according to the Newton's Second
Law:

m·g − k·x(t) = m·x"(t)

This is the differential equation that defines the movement of our object.



We don't have to resort to modifying this differential equation with an
approximate one to be able to solve it. It is fully solvable and the
general solution of this linear differential equation of the second
order is

x(t) = C₁·cos(t·√k/m) +

+ C₂·sin(t·√k/m) + m·g/k



Now we can apply the initial conditions to determine constants C₁ and C₂.

Since x(0) = L,

C₁ = L − m·g/k

Since x'(0) = 0,

C₂ = 0



This produces the following expression for x(t):

x(t) = (L − m·g/k)·cos(t·√k/m) +

+ m·g/k



Interestingly, if

L − m·g/k = 0 or L·k = m·g

(which means that the weight W=m·g is balanced by the force of spring's elasticity F=−L·k in its initial position with our object at its end) then there are no oscillations, and the object will remain at distance L=m·g/k from a spring's neutral position.



If there are oscillations, their period is

T = 2π√m/k