Problems on LC Circuits: UNIZOR.COM - Physics4Teens - Electromagnetism -...

Notes to a video lecture on http://www.unizor.com

Problems on LC Circuit

Problem A

Consider a circuit that contains an AC generator, an inductor of inductance L and a capacitor of capacity C in a series.


Generated EMF has frequency f=50Hz and effective voltage E_eff=220V (volt).
The effective AC current is I_eff=5A (ampere).
The capacitance of a capacitor is C=10μF (microfarad).
Find inductance L (henry) of an inductor?

Solution

Let's start with an expression for the AC current in the LC circuit in terms of generated EMF and reactance of the capacitor and inductor.

EDF generated by a source of electricity
E(t) = E₀·sin(ωt)
where
E₀ is a peak voltage on the terminals of a generator,
ω=2πf is an angular velocity of a rotor in radians per second, where f is a frequency of generated EMF in number of cycles per second.

Alternating electric current in the circuit
I(t) = I₀·cos(ωt)
where
I₀ = E₀/(X_C−X_L) is peak amperage,
X_C = 1/(ω·C) is capacitive reactance,
X_L = ω·L is inductive reactance

Effective voltage and effective amperage are less than, correspondingly, peak voltage and peak amperage by √2.
Therefore, from the expression for AC current follows
I(t) = I₀·cos(ωt) =
= E₀·cos(ωt)/(X_C−X_L)
I_eff = I₀/√2 =
= E₀/[√2(X_C−X_L)] =
= E_eff/(X_C−X_L)

The unknown in this expression is X_L that can be found:
X_C−X_L = E_eff/I_eff
X_L = X_C−E_eff/I_eff

Since X_C=1/(ω·C) and X_L=ω·L L·ω = 1/(ω·C) − E_eff/I_eff
L = 1/(ω²·C) − E_eff/(ω·I_eff)

Substituting
ω=2πf=2π·50Hz=314(1/sec)
C=10μF=10⁻⁵F
E_eff=220V
I_eff=5A
into above expression for L, we obtain (rounded to 0.001)
L= 1/(314²·10⁻⁵)−220/(314·5)=
= 0.874H (henry)


Problem B

Consider a circuit that contains a source of a noisy electrical signal, which is a combination of many sinusoidal waves with different frequencies, amplitudes and phase shifts, a resistor with resistance R and a capacitor with capacitance C connected parallel to a resistor.


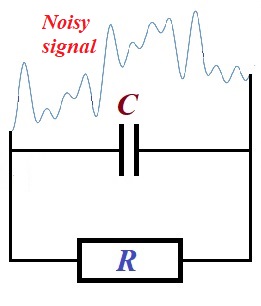
The signal (electrical current) coming through a resistor will have higher frequencies weakened by a presence of a capacitor.
Explain why.

Explanation

Reactance of a capacitor X_C, which functionally similar to a resistance of a resistor, is inversely proportional to a frequency of the voltage on its ends
X_C = 1/(ω·C) = 1/(2πf·C),
where
ω=2πf is the angular velocity of oscillations,
f is a frequency of oscillations,
C is the capacitance of a capacitor.
Therefore, the greater frequency - the less reactance of a capacitor.
Since reactance of a capacitor is functionally similar to a resistance of a resistor, this circuit is similar to a circuit with two parallel resistors with one of them having lower resistance with higher frequencies of the oscillations of the electrical current.

Using this analogy, we see that higher frequency oscillations of the electric current going through a capacitor will meet less resistance than lower frequency oscillations. Therefore, higher frequency oscillations of the current will go easier through a capacitor, thus having less impact on a resistor.

More precisely, the current going through parallel resistors is inversely proportional to their resistance (see lecture "DC Ohm's Law" in this part of the course). This is true not only for constant direct current produced by constant EMF E, but also at any moment t, when generated EMF oscillates (even irregularly) as a function of time E(t).
Therefore, a capacitor will lower reactance will have higher current going through it, thus weakening the higher frequency oscillations of the current going through a resistor.

Problem C

Consider a circuit that contains a source of a noisy electrical signal, which is a combination of many sinusoidal waves with different frequencies, amplitudes and phase shifts, a resistor with resistance R and an inductor with inductance L connected parallel to a resistor.


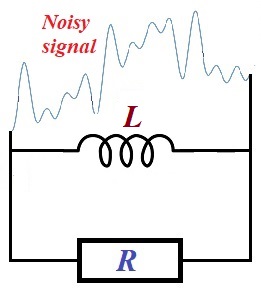
The signal (electrical current) coming through a resistor will have lower frequencies weakened by a presence of a inductor.
Explain why.

Explanation

Reactance of an inductor X_L, which functionally similar to a resistance of a resistor, is proportional to a frequency of the voltage on its ends
X_L = ω·L = 2πf·L,
where
ω=2πf is the angular velocity of oscillations,
f is a frequency of oscillations,
L is the inductance of an inductor.
Therefore, the lower frequency - the less reactance of an inductor.
Since reactance of an inductor is functionally similar to a resistance of a resistor, this circuit is similar to a circuit with two parallel resistors with one of them having lower resistance with lower frequencies of the oscillations of the electrical current.

Using this analogy, we see that lower frequency oscillations of the electric current going through an inductor will meet less resistance than higher frequency oscillations. Therefore, lower frequency oscillations of the current will go easier through an inductor, thus having less impact on a resistor.

More precisely, the current going through parallel resistors is inversely proportional to their resistance (see lecture "DC Ohm's Law" in this part of the course). This is true not only for constant direct current produced by constant EMF E, but also at any moment t, when generated EMF oscillates (even irregularly) as a function of time E(t).
Therefore, an inductor will lower reactance will have higher current going through it, thus weakening the lower frequency oscillations of the current going through a resistor.

SUMMARY
Capacitors and inductors can be used to filter certain "useful" frequencies from the noisy signals.

Series LC Circuit: UNIZOR.COM - Physics4Teens - Electromagnetism - Alter...

Notes to a video lecture on http://www.unizor.com



Series LC Circuit



Consider a circuit that contains an AC generator, an inductor of inductance L and a capacitor of capacity C in a series.




The current I_L(t) going through an inductor is the same as the current I_C(t) going through a capacitor. So, we will use an expression I(t) for both.



The electromotive force (EMF) generated by an AC generator depends only
on its own properties and can be described as a function of time t

E(t) = E₀·sin(ωt)

where

E₀ is a peak voltage on the terminals of a generator,

ω is an angular velocity of a rotor in radians per second.



Inductance L of an inductor and capacity C of a capacitor produce voltage drops V_L(t) and V_C(t) correspondingly.



As we know, the voltage drop on an inductor is causes by self-induction
and depends on the rate of change (that is, the first derivative by
time) of a magnetic flux Φ(t) going through it

V_L(t) = dΦ(t)/dt

Magnetic flux, in turn, depends on a current going through a wire of an inductor I(t) and the inductor's inductance L

Φ(t) = L·I(t)

Therefore, the voltage drop on an inductor equals to

V_L(t) = L·dI(t)/dt



As we know, the amount of electricity Q(t) accumulated in a capacitor is proportional to voltage V_C(t) applied to its plates (that is, voltage drop on a capacitor). The constant capacity of a capacitor C
is the coefficient of proportionality (see lecture "Electric Fields" -
"Capacitors" in this course) that depends on a type of a capacitor

C = Q(t)/V_C(t)

Therefore,

Q(t)=C·V_C(t)



Knowing the amount of electricity Q(t) accumulated in a capacitor as a function of time t, we can determine the electric current I(t) in a circuit, which is a rate of change (that is, the first derivative by time) of the amount of electricity

I(t) = dQ(t)/dt = C·dV_C(t)/dt



The sum of voltage drops on an inductor and a capacitor is supposed to be equal to EMF produced by an AC generator E(t)=E₀·sin(ωt), which is the final equation in our system:

V_L(t) = L·dI(t)/dt

I(t) = C·dV_C(t)/dt

E₀·sin(ωt) = V_L(t) + V_C(t)



To solve this system of three equations, including two differential ones, let's resolve the third equation for V_C(t) and substitute it in the second one.

V_C(t) = E₀·sin(ωt) − V_L(t)

I(t)=C·d[E₀·sin(ωt)−V_L(t)]/dt



In the last equation we can differentiate each component and, using symbol ' for a derivative, obtain

I(t)=CωE₀·cos(ωt)−C·V'_L(t)



Together with the first equation from the original system of three
equations above we have reduced the system to two equations (again, we
use symbol ' for brevity to signify differentiation)

V_L(t) = L·I'(t)

I(t)=CωE₀·cos(ωt)−C·V'_L(t)



Substituting V_L(t) from the first of these equations into the second, we obtain one equation for I(t), which happens to be a differential equation of the second order (we will use symbol " to signify a second derivative of I(t) for brevity)

I(t)=CωE₀·cos(ωt)−CL·I"(t)

or in a more traditional for differential equation form

a·I"(t) + b·I(t) = E₀·cos(ωt)

where

a = L/ω

b = 1/(Cω)



Without getting too deep into a theory of differential equations, notice that the one and only known function in this equation that depends on time t is cos(ωt). It's second derivative also contains cos(ωt). So, if I(t) is proportional to cos(ωt), its second derivative I"(t) will also be proportional to cos(ωt) and we can find the coefficient of proportionality to satisfy the equation.



Let's try to find such coefficient K that function I(t)=K·cos(ωt) satisfies our equation.

I'(t) = −ωK·sin(ωt)

I"(t) = −ω²K·cos(ωt)



Now our differential equation for I(t) is

−a·ω²K·cos(ωt) + b·K·cos(ωt) = E₀·cos(ωt)



From this we can easily find a coefficient K

K = E₀/(b−aω²)



Since a=L/ω and b=1/(Cω)

K = E₀/{[1/(Cω)] − Lω}



In the previous lectures we have introduced concepts of capacitive reactance X_C=1/(Cω) and inductive reactance X_L=Lω. Using these variables, the expression for coefficient K is
K = E₀/(X_C−X_L)

Therefore,

I(t) = E₀·cos(ωt)/(X_C−X_L)

or

I(t) = I₀·cos(ωt)

where

I₀ = E₀/(X_C−X_L)



The last equation brings us to a concept of a reactance of the LC circuit

X_C−X_L

that is similar to resistance of regular resistors.

Using a concept of reactance, the last equation resembles the Ohm's Law.



Let's determine the voltage drops on a capacitor V_C(t) and an inductor V_L(t) using the expression for the current I(t).



Since Q(t)=C·V_C(t) and I(t)=Q'(t), we can find V_C(t) by integrating I(t)/C.

V_C(t) = ∫_[0,t]I(t)·dt/C =

= I₀·sin(ωt)/(C·ω) =

= X_C·E₀·sin(ωt)/(X_C−X_L)



V_L(t) = L·I'(t) =

= −L·E₀·sin(ωt)·ω/(X_C−X_L) =

= −X_L·E₀·sin(ωt)/(X_C−X_L)



Let's check that the sum of voltage drops in the circuit V_L(t) and V_C(t) is equal to the original EMF generated by a source of electricity.

Indeed,

V_L(t) + V_C(t) =

=(X_C−X_L)·E₀·sin(ωt)/(X_C−X_L)=

= E₀·sin(ωt)



Summary



EDF generated by a source of electricity

E(t) = E₀·sin(ωt)

where

E₀ is a peak voltage on the terminals of a generator,

ω is an angular velocity of a rotor in radians per second.



Alternating electric current in the circuit

I(t) = I₀·cos(ωt)

where

I₀ = E₀/(X_C−X_L)

X_C = 1/(ω·C)

X_L = ω·L



Voltage drop on a capacitor

V_C(t) = X_C·E₀·sin(ωt)/(X_C−X_L)



Voltage drop on an inductor

V_L(t) = −X_L·E₀·sin(ωt)/(X_C−X_L)



Phase Shift



Notice that cos(x)=sin(x+π/2). Graph of function y=sin(x+π/2) is shifted to the left by π/2 relative to graph of y=sin(x).

Therefore, oscillations of the current I(t) in the LC circuit are ahead of oscillation of the EMF generated by a source of electricity E(t) by a phase shift of π/2.



Oscillations of the voltage drop on a capacitor V_C(t) in the LC circuit are synchronized (in phase) with generated EMF.



Notice that −sin(x)=sin(x+π). Graph of function y=sin(x+π) is shifted to the left by π relative to graph of y=sin(x).

Therefore, oscillations of the voltage drop on an inductor V_L(t) in the LC circuit are ahead of oscillation of the EMF generated by a source of electricity E(t) by π (this is called in antiphase).

AC Inductors: UNIZOR.COM - Physics4Teens - Electromagnetism

Notes to a video lecture on http://www.unizor.com



Alternating Current and Inductors



For the purpose of this lecture it's important to be familiar with the concept of a self-induction explained in "Electromagnetism - Self-Induction" chapter of this course.



In this lecture we will discuss the AC circuit that contains an inductor - a wire wound in a reel or a solenoid, thus making multiple loops, schematically presented on the following picture.





Both direct and alternating current go through an inductor, but, while
direct current goes with very little resistance through a wire, whether
it's in a shape of a loop or not, alternating current meets some
additional resistance when this wire is wound into a loop.



Consider the following experiment.





Here the AC circuit includes a lamp, an inductor in a shape of a solenoid and an iron rod fit to be inserted into a solenoid.

While the rod is not inside a solenoid, the lamp lights with normal
intensity. But let's gradually insert an iron core into a solenoid. As
the core goes deeper into a solenoid, the lamp produces less and less
light, as if some kind of resistance is increasing in the circuit.

This experiment demonstrates that inductors in the AC circuit produce
effect similar to resistors, and the more "inductive" the inductor - the
more resistance can be observed in a circuit.

The theory behind this is explained in this lecture.



The cause of this resistance is self-induction. This concept was
explained earlier in this course and its essence is that variable
magnetic field flux, going through a wire loop, creates electromotive
force (EMF) directed against the original EMF that drives electric
current through a loop.



Any current that goes along a wire creates a magnetic field around this
wire. Since the current in our wire loop is alternating, the magnetic
field that goes through this loop is variable. According to the
Faraday's Law, the variable magnetic field going through a wire loop
generates EMF equal to a rate of change of the magnetic field flux and
directed opposite to the EMF that drives the current through a wire,
thus resisting it.



Magnetic flux Φ(t) going through inductor, as a function of time t, is proportional to an electric current I(t) going through its wire

Φ(t) = L·I(t)

where L is a coefficient of proportionality that depends
on physical properties of the inductor (number of loop in a reel, type
of its core etc.) called inductance of the inductor.



If the current is alternating as

I(t) = I_max·sin(ωt)

the flux will be

Φ(t) = L·I_max·sin(ωt)



According to Faraday's Law, self-induction EMF E_i
is equal in magnitude to a rate of change of magnetic flux and opposite
in sign (see chapter "Electromagnetism - "Self-Induction" in this
course)

E_i(t) = −dΦ/dt =

= −L·dI(t)/dt =

= −L·ω·I_max·cos(ωt) =

= −L·ω·I_max·sin(ωt+π/2) =

= −E_imax·sin(ωt+π/2)

where

E_imax = L·ω·I_max



The unit of measurement of inductance is henry (H) with 1H being an inductance of an inductor that generates 1V electromotive force, if the rate of change of current is 1A/sec.

That is,

henry = volt·sec/ampere = ohm·sec



An expression X_L=L·ω in the above formula for E_i is called inductive reactance. It plays the same role for an inductor as resistance for resistors.

The units of the inductive reactance is Ohm (Ω) because

henry/sec = ohm·sec/sec = ohm.



Using this concept of inductive reactance X_L of an inductor, the time dependent induced EMF is

E_i(t) = −X_L·I_max·sin(ωt+π/2) = −E_imax·sin(ωt+π/2)

and

E_imax = X_L·I_max,

which for inductors in AC circuit is an analogue of the Ohm's Law for resistors.



What's most important in the formula

E_i(t) = −E_imax·sin(ωt+π/2)

and the most important property of an inductor in an AC circuit is
that, while the electric current in a circuit oscillates with angular
speed ω, the voltage drop on an inductor oscillates with the same angular speed ω as the current, but its period is shifted in time by π/2 relative to the current.