Notes to a video lecture on http://www.unizor.com
Series LC Circuit
Consider a circuit that contains an AC generator, an inductor of inductance L and a capacitor of capacity C in a series.
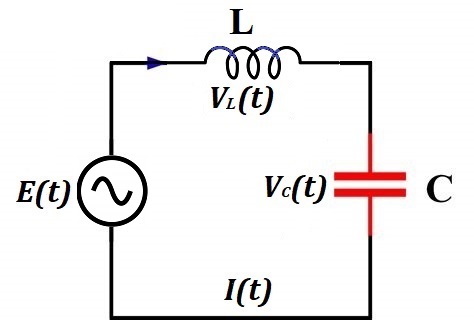
The current IL(t) going through an inductor is the same as the current IC(t) going through a capacitor. So, we will use an expression I(t) for both.
The electromotive force (EMF) generated by an AC generator depends only
on its own properties and can be described as a function of time t
E(t) = E0·sin(ωt)
where
E0 is a peak voltage on the terminals of a generator,
ω is an angular velocity of a rotor in radians per second.
Inductance L of an inductor and capacity C of a capacitor produce voltage drops VL(t) and VC(t) correspondingly.
As we know, the voltage drop on an inductor is causes by self-induction
and depends on the rate of change (that is, the first derivative by
time) of a magnetic flux Φ(t) going through it
VL(t) = dΦ(t)/dt
Magnetic flux, in turn, depends on a current going through a wire of an inductor I(t) and the inductor's inductance L
Φ(t) = L·I(t)
Therefore, the voltage drop on an inductor equals to
VL(t) = L·dI(t)/dt
As we know, the amount of electricity Q(t) accumulated in a capacitor is proportional to voltage VC(t) applied to its plates (that is, voltage drop on a capacitor). The constant capacity of a capacitor C
is the coefficient of proportionality (see lecture "Electric Fields" -
"Capacitors" in this course) that depends on a type of a capacitor
C = Q(t)/VC(t)
Therefore,
Q(t)=C·VC(t)
Knowing the amount of electricity Q(t) accumulated in a capacitor as a function of time t, we can determine the electric current I(t) in a circuit, which is a rate of change (that is, the first derivative by time) of the amount of electricity
I(t) = dQ(t)/dt = C·dVC(t)/dt
The sum of voltage drops on an inductor and a capacitor is supposed to be equal to EMF produced by an AC generator E(t)=E0·sin(ωt), which is the final equation in our system:
VL(t) = L·dI(t)/dt
I(t) = C·dVC(t)/dt
E0·sin(ωt) = VL(t) + VC(t)
To solve this system of three equations, including two differential ones, let's resolve the third equation for VC(t) and substitute it in the second one.
VC(t) = E0·sin(ωt) − VL(t)
I(t)=C·d[E0·sin(ωt)−VL(t)]/dt
In the last equation we can differentiate each component and, using symbol ' for a derivative, obtain
I(t)=CωE0·cos(ωt)−C·V'L(t)
Together with the first equation from the original system of three
equations above we have reduced the system to two equations (again, we
use symbol ' for brevity to signify differentiation)
VL(t) = L·I'(t)
I(t)=CωE0·cos(ωt)−C·V'L(t)
Substituting VL(t) from the first of these equations into the second, we obtain one equation for I(t), which happens to be a differential equation of the second order (we will use symbol " to signify a second derivative of I(t) for brevity)
I(t)=CωE0·cos(ωt)−CL·I"(t)
or in a more traditional for differential equation form
a·I"(t) + b·I(t) = E0·cos(ωt)
where
a = L/ω
b = 1/(Cω)
Without getting too deep into a theory of differential equations, notice that the one and only known function in this equation that depends on time t is cos(ωt). It's second derivative also contains cos(ωt). So, if I(t) is proportional to cos(ωt), its second derivative I"(t) will also be proportional to cos(ωt) and we can find the coefficient of proportionality to satisfy the equation.
Let's try to find such coefficient K that function I(t)=K·cos(ωt) satisfies our equation.
I'(t) = −ωK·sin(ωt)
I"(t) = −ω²K·cos(ωt)
Now our differential equation for I(t) is
−a·ω²K·cos(ωt) + b·K·cos(ωt) = E0·cos(ωt)
From this we can easily find a coefficient K
K = E0/(b−aω²)
Since a=L/ω and b=1/(Cω)
K = E0/{[1/(Cω)] − Lω}
In the previous lectures we have introduced concepts of capacitive reactance XC=1/(Cω) and inductive reactance XL=Lω. Using these variables, the expression for coefficient K is
K = E0/(XC−XL)
Therefore,
I(t) = E0·cos(ωt)/(XC−XL)
or
I(t) = I0·cos(ωt)
where
I0 = E0/(XC−XL)
The last equation brings us to a concept of a reactance of the LC circuit
XC−XL
that is similar to resistance of regular resistors.
Using a concept of reactance, the last equation resembles the Ohm's Law.
Let's determine the voltage drops on a capacitor VC(t) and an inductor VL(t) using the expression for the current I(t).
Since Q(t)=C·VC(t) and I(t)=Q'(t), we can find VC(t) by integrating I(t)/C.
VC(t) = ∫[0,t]I(t)·dt/C =
= I0·sin(ωt)/(C·ω) =
= XC·E0·sin(ωt)/(XC−XL)
VL(t) = L·I'(t) =
= −L·E0·sin(ωt)·ω/(XC−XL) =
= −XL·E0·sin(ωt)/(XC−XL)
Let's check that the sum of voltage drops in the circuit VL(t) and VC(t) is equal to the original EMF generated by a source of electricity.
Indeed,
VL(t) + VC(t) =
=(XC−XL)·E0·sin(ωt)/(XC−XL)=
= E0·sin(ωt)
Summary
EDF generated by a source of electricity
E(t) = E0·sin(ωt)
where
E0 is a peak voltage on the terminals of a generator,
ω is an angular velocity of a rotor in radians per second.
Alternating electric current in the circuit
I(t) = I0·cos(ωt)
where
I0 = E0/(XC−XL)
XC = 1/(ω·C)
XL = ω·L
Voltage drop on a capacitor
VC(t) = XC·E0·sin(ωt)/(XC−XL)
Voltage drop on an inductor
VL(t) = −XL·E0·sin(ωt)/(XC−XL)
Phase Shift
Notice that cos(x)=sin(x+π/2). Graph of function y=sin(x+π/2) is shifted to the left by π/2 relative to graph of y=sin(x).
Therefore, oscillations of the current I(t) in the LC circuit are ahead of oscillation of the EMF generated by a source of electricity E(t) by a phase shift of π/2.
Oscillations of the voltage drop on a capacitor VC(t) in the LC circuit are synchronized (in phase) with generated EMF.
Notice that −sin(x)=sin(x+π). Graph of function y=sin(x+π) is shifted to the left by π relative to graph of y=sin(x).
Therefore, oscillations of the voltage drop on an inductor VL(t) in the LC circuit are ahead of oscillation of the EMF generated by a source of electricity E(t) by π (this is called in antiphase).


No comments:
Post a Comment