Notes to a video lecture on http://www.unizor.com
Rotational Kinematics
So far we were mostly considering translational motion of point-objects - a motion along a straight line with or without external forces acting upon this object.
Rotational motion obeys the rules in many respects analogous to the laws of translational motion, except we have to change linear movement to rotation.
Consider a point-object m connected by a rigid rod of the length r to an axis, around which this object can rotate within a plane of rotation that is perpendicular to an axis of rotation.
The picture below illustrates such a movement and also indicates the position of angular velocity ω of a rotation, which we will explain later.
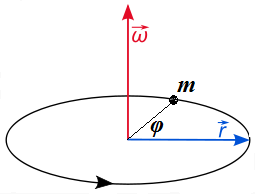
Let's discuss the similarities and differences between translational movement along a straight line and rotation around an axis within a plane perpendicular to this axis (a plane of rotation).
The first main concept of translational motion is position or distance from the beginning of motion (for a straight line movement) as a function of time. In rotational motion its equivalent is angle of rotation from some original position as a function of time.
| Translation | Rotation |
| Distance s(t) | Angle φ(t) |
The next concept is speed or (better) velocity of translational motion. This is a first derivative of position (or distance) by time:
v(t) = s'(t).
Its equivalent for rotational motion is angular speed, which is a first derivative of angle of rotation by time:
ω(t) = φ'(t)
While vector character of speed of translational motion is obvious and is reflected in the term velocity, vector character of angular speed is less obvious.
The angle of rotation from the first glance is a scalar function of time. But only from the first glance.
In theory, rotational motion always assumes existence of an axis of
rotation and a plane of rotation. To reflect these characteristics and a
magnitude of angular speed, an angular speed is represented by a vector
from a center of rotation along an axis of rotation perpendicularly to a
plane of rotation with a magnitude equal to a value of angular speed.
This allows to represent the rotation in its full spectrum of
characteristics - magnitude, axis, plane of rotation. The picture above
represents angular speed as a vector ω(t), which we may call angular velocity vector.
There is one more characteristic of rotational motion not yet discussed - its direction. It is also reflected in angular velocity
as a vector by its direction. In theory, we can choose two different
directions along the axis of rotation. The direction chosen is such
that, if we look from its end onto a plane of rotation, the rotation is
counterclockwise. Another interpretation of this is the "rule of the
right hand" because if you put you right hand on a plane of rotation
such that your finger go around the axis of rotation pointing to a
direction of rotation, your thumb points to a direction of the angular velocity vector.
So, angular velocity vector represents axis, plane, direction of rotation as well as magnitude of angular speed.
To be more precise, since this vector representation of angular velocity is a little unusual, it is customary to call it "pseudo-vector" instead of "vector".
During infinitesimal time interval dt an object rotating around an axis on a radius r turns by an angle dφ(t), covering the distance ds(t)=r·dφ(t) (this is the length of an arc of radius r and angle dφ, according to a known formula of geometry).
From this follows:
ds(t)/dt = r·dφ(t)/dt or
v(t) = r·ω(t)
| Translation | Rotation |
| Speed v(t)=s'(t) v(t)=r·ω(t) | Angular Speed ω(t)=φ'(t) ω(t)=v(t)/r |
The next concept is acceleration that needs its rotational analogue. Obviously, it's the first derivative of angular velocity or the second derivative of an angle of rotation by time.
Using the vector interpretation of angular velocity, we can consider angular acceleration as a vector as well. It is also directed along the axis of rotation.
During infinitesimal time interval dt an angular velocity ω(t) changes by dω(t).
From this follows relationship between linear acceleration a and angular acceleration α:
a(t) = dv(t)/dt = r·dω(t)/dt or
a(t) = r·α(t)
| Translation | Rotation |
| Acceleration a(t)=v'(t) a(t)=r·α(t) | Angular Acc. α(t)=ω'(t) α(t)=a(t)/r |
Obviously, integrating the definitions of angular velocity ω and angular acceleration α for constant angular acceleration, we come up with formulas similar to those familiar from translational movement:
ω(t) = ω(0) + α·t
φ(t) = φ(0) + ω(0)·t + α·t²/2
Angular acceleration as a vector (as a pseudo-vector, to be exact), is colinear to the axis of rotation, because angular velocity is.
If rotation goes as on the above picture and the speed of rotation increases, the angular acceleration would be directed upwards, the same way as the angular velocity.


No comments:
Post a Comment