Notes to a video lecture on http://www.unizor.com
Moment of Inertia
Recall the rotational equivalent of the Newton's Second Law:
τ = I·α
where
τ = F·r - a torque, a product of tangentially applied force F and the distance from the point of application of force to the axis of rotation r;
I = m·R² - a moment of inertia, a product of inertial mass of a point-object by a square of its distance from the axis of rotation R (might be different from the distance r above);
α - angular acceleration of rotation.
It is very important to correspond straight line translational elements of motion with their rotational counterparts:
| Translation | Rotation |
| Force F | Torque τ = F·r |
| Linear Acceleration a | Angular Acceleration α = a/r |
| Inertial Mass m | Moment of Inertia I = m·r² |
| Newton's Second Law F=m·a | Rotational Equivalent τ = I·α |
In this lecture we will study the moment of inertia and its properties. We will also calculate the moment of inertia in a few simple cases.
The first very important property of the moment of inertia is that it is additive.
It means that the moment of inertia of two rigidly connected
point-objects rotating around the same axis of rotation equals to sum of
their individual moments of inertia.
Let's explain why.
Consider a rigid weightless disk rotating around an axis going through
its center perpendicularly to it and two point-objects of mass m1 and m2 fixed on its surface at distances, correspondingly, r1 and r2.
Assume that this disk with both fixed on it objects is rotating with angular acceleration α caused by some force F acting on a distance R from its center tangentially to a circle of a radius R within a plane of this disk.
The picture below illustrates this.
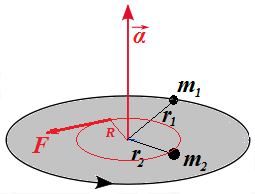
Our purpose is to explain that the combined moment of inertia of both objects equals to a sum of their corresponding individual moments of inertia.
The fact that object of mass m1 on a distance r1 from the axis of rotation has angular acceleration α implies that there is a force f1 acting on it tangentially to its trajectory such that (from rotational equivalent of the Newton's Second Law):
f1·r1 = I1·α
where I1=m1·r1² - moment of inertia of this object.
Similarly, the fact that object of mass m2 on a distance r2 from the axis of rotation has angular acceleration α implies that there is a force f2 acting on it tangentially to its trajectory such that (from rotational equivalent of the Newton's Second Law):
f2·r2 = I2·α
where I2=m2·r2² - moment of inertia of this object.
Behavior of this system depends only on parameters specified above -
masses, distances from the center of a disk and forces. So, if we change
the initial position of masses without changing their distances from
the center, the system will work exactly the same.
Our first modification then will be to shift the position of mass m2 along its circular trajectory of radius r2 to a position, where it is on the same radius as m1. So, both masses and a center of a disk are on one line.
Similarly, let's shift the point of application of force F to a point on the same line where our two objects are now located without changing the distance R
from the point of application of the force to a center. Now both masses
and a point of application of main force that rotates the disk are on
the same line with a center of the disk, while their distances from a
center are still the same as before.
As we know, the angular acceleration of a rotating object depends on its
mass, its distance from an axis of rotation and a torque of a force
rotating this object.
If force f1 applied directly to an object of mass m1 located on a distance r1 from the axis of rotation caused the angular acceleration α, any other force having the same torque τ1=f1·r1 would result in the same angular acceleration.
Let's replace then the force f1 acting on a distance r1 from the axis with force g1=f1·r1/R, acting on a distance R at the point where our main force F was applied. There will be no change in angular acceleration since the torque acting on our object is the same:
τ'1 = (f1·r1/R)·R = f1·r1 = τ1
Same trick with the second object results in using force g2=f2·r2/R, acting on a distance R at the point where our main force F was applied, with no change in the behavior of the system.
τ'2 = (f2·r2/R)·R = f2·r2 = τ2
We have brought all forces (g1, g2 and F)
to the same point of application. They act in the same direction -
tangentially to a circular trajectory. We know that the effect of main
force F applied to this point is equivalent to a combined effect of forces g1=f1·r1/R and g2=f2·r2/R applied to the same point in the same direction. Therefore, sum of forces g1 and g2 must be equal to force F:
g1 + g2 = F
Now what remains is simple algebra.
f1·r1/R + f2·r2/R = F
f1·r1 + f2·r2 = F·R
τ1 + τ2 = F·R
I1·α + I2·α = F·R
(I1 + I2)·α = F·R
The expression on the right is the torque of the main force F acting tangentially to a circle of rotation on a distance R from the axis:
τ = F·R
Therefore, the expression on the left, according to rotational equivalent of the Newton's Second Law, must be a moment of inertia of the entire system I multiplied by the system's angular acceleration α:
I·α = τ = F·R
from which follows the equality
I·α = (I1 + I2)·α
and, finally,
I = I1 + I2
That means that the combined moment of inertia of two objects equals to a sum of their individual moments of inertia.
In short, moment of inertia is additive.
The most important consequence of this is that, to calculate a moment of
inertia of a rotating solid object of some complicated geometric shape,
we can divide it in small (strictly speaking, infinitesimally small)
pieces, calculate a moment of inertia of each piece and add all these
moments of inertia together (strictly speaking, integrating them) to get
a moment of inertia of the whole rotating solid object.
Let's calculate a moment of inertia of some solids, using this approach.
1. Rod rotating around its edge
Consider a solid thin rod of a length L and mass m rotating around an axis that is perpendicular to it and going through its one end.
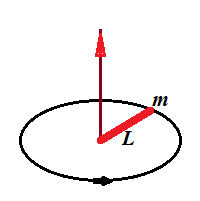
To calculate its moment of inertia, we divide it in small pieces of the length dr, located on a distance r from the axis and having mass dm=(m/L)·dr.
Each such piece has a moment of inertia
dI = (dm)·r² = (m/L)·r²·dr
Since moment of inertia is additive, all we have to do now is to integrate this by r from 0 to L.
The indefinite integral of function r² is r³/3. So, by Newton-Leibniz formula the result of integration on an interval [0,L] is
L³/3 − 0³/3 = L³/3.
So, the total moment of inertia of a rod is
Irod = (m/L)·L³/3 = m·L²/3
2. Rod rotating around its center
Let's calculate the moment of inertia, if the rod rotates around its center point.
We can consider now this rod as a system of two small half-rods, each being a half of the original one, with length L/2 and mass m/2.
Each half-rod rotates around its end, so the formula above is applicable to each half-rod.
Its moment of inertia is
Ihalf = (m/2)·(L/2)²/3 = m·L²/24
The whole rod, being a system of two half-rods, has a momentum of
inertia equal to a sum of momentums of its two halves, so its value is
double of the above moment of inertia for each half-rod:
Iwhole = m·L²/12


No comments:
Post a Comment