Notes to a video lecture on http://www.unizor.com
Equilibrium of Solids
As we know, if a vector sum of forces, acting on a point-object, equals
to null-vector, this point-object is at rest or in a state of uniform
motion along a straight line in any inertial frame of reference.
Alternatively, we can say that a frame of reference associated with this
point-object is inertial.
The complexity of a concept of equilibrium of solids lies in the fact
that, even if vector sum of forces, acting on a solid, equals to
null-vector, this solid might not be in the state of rest in any
inertial system. In a simple case of two forces, equal in magnitude and
opposite in direction, applied to two different points of a solid, will
rotate it, making a frame of reference associated with it non-inertial.
Any rotation of a solid, however complex, can be represented as a
combination of three rotations around three coordinate axes. Therefore, a
solid in a state of equilibrium should be in equilibrium relative to
each coordinate axis, and, to study equilibrium of a solid in
three-dimensional space, it is sufficient to study it relative to one
axis.
As we know, in case of rotation around an axis, the main factor replacing a concept of force for translational movement, is torque. Since torque is a cause of rotation, the necessary condition to prevent a rotation is balancing of torques.
Torque is a vector equal to a vector (cross) product of a radius-vector r from the axis of rotation to a point of application of force (perpendicularly to the axis) by a vector of force:
τ = r×F
Using this concept of torque, we can formulate the following necessary condition for an equilibrium of a solid.
Sum of torques of all forces acting on a solid relative to each coordinate axis must be equal to null-vector.
In the previous lecture we introduced a concept of a degree of freedom
and, in particular, mentioned six degrees of freedom of a solid: three
degrees of freedom along each coordinate axis and three degrees of
freedom of rotation around each coordinate axis.
If a vector sum of all forces acting on a solid is a null-vector, there
will be a point that is not moving anywhere or, more precisely, a frame
reference associated with this point is inertial. This condition assures
an equilibrium by three degrees of freedom associated with
translational motion (a motion along coordinate axes).
If a vector sum of all torques relatively to each of the three
coordinate axes is a null-vector, there will be no rotation and the
system will be in equilibrium by three other degrees of freedom
associated with rotational motion (a motion around coordinate axes).
So, for a solid to be in equilibrium, the necessary conditions are
all of the above - sum of all the forces and sum of all the torques must
be null-vectors.
Consider the following example.
A weightless rod of a length 2r is hanging horizontally on a thread fixed at its midpoint.
On both ends of a rod there are equal weights W hanging down.
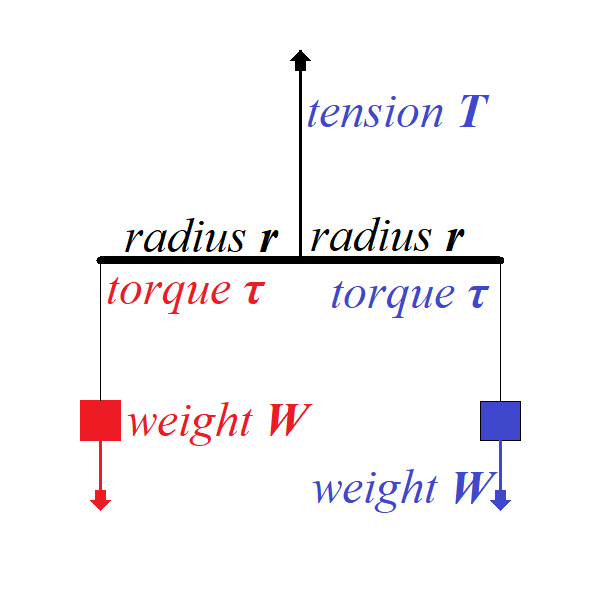
To balance the translational movement of a system vertically down the force of tension T on a thread that holds the rod must balance a sum of forces of weight acting in opposite direction:
T + W + W = 0
T = −2W
To balance the rotational movement of a system around a midpoint of a
rod the torque of one weight should be equal in magnitude to the torque
of another weight since the directions of these two torques are
opposite:
τ blue = r ×W
τ red = −r ×W
τ red + τ blue = 0
Consider a less symmetrical case below.
Here a rod of the length 3r is hanging by a thread fixed not in the middle, but at a distance r from the left edge and, therefore, at a distance 2r from the right edge.
At the same time, the weight on the left is twice as heavy as the one on the right.
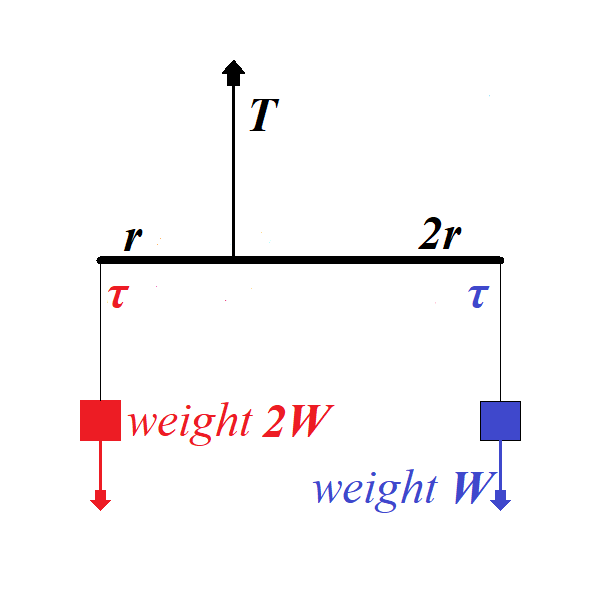
Tension on the thread holding a rod must be greater to hold more weight:
T + W + 2W = 0
T = −3W
From the rotational viewpoint, this system is in equilibrium because the
torques on the left of a rod and on the right are equal in magnitude,
while opposite in direction:
τ blue = 2r ×W
τ red = −r ×2W
τ red + τ blue = 0


No comments:
Post a Comment