Notes to a video lecture on http://www.unizor.com
Problems on Equilibrium
Problem 1
Two point-objects of mass M and m are hanging at two opposite ends of a weightless rod of length L.
At what point on a rod should we fix a thread, so the system of a rod with two weights is hanging on this thread in equilibrium?
Does this state of equilibrium imply that a rod is horizontal?
Answer
At distance m·L /(M+m) from the end with object of mass M.
Problem 2
An object of weight W is positioned on a flat surface. The coefficient of static friction is μ.
What is the minimum pulling force P to be applied to a
rope, attached to this object, to start pulling it forward, if the angle
between a rope and a horizontal flat surface is φ?
Answer
P = μ·W / [cos(φ)+μ·sin(φ)]
Problem 3
Consider the following illustration to this problem.
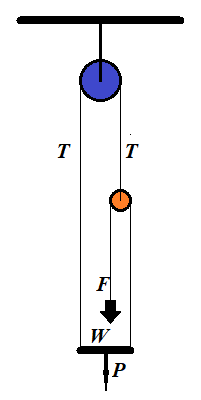
A person of weight W stands on a platform of weight P. Pulleys and ropes are arranged as on this illustration.
What is the force F a person should apply to a rope to keep the whole system in equilibrium?
Solution
Let N be a reaction of a platform onto a person. It pushes the person upward.
If F is a force of a person pulling a rope down, and the
system is in equilibrium, that is all components are at rest and all
forces are balanced, the rope pulls a person up with the same force F, according to the Third Newton's Law.
Since a person is in equilibrium, forces directed upward (N+F) should be equal in magnitude to forces directed downwards (weight of the person W):
N+F = W
The platform is also in equilibrium. The forces that push it down are its weight P and reaction N of a person standing on it. The forces pulling the platform up are tensions of two ropes T on the left and F on the right:
P+N = T+F
Finally, a small pulley is in equilibrium. It's pulled down by two tensions F, from the left and from the right. The tension T pulls it up:
T = 2F
We have three equations with three unknowns: T, N and F, which we have to solve for an unknown force F, with which a person pulls a rope to balance the system:
Substituting T from the last equation into the second one, getting a system of two equations:
N+F = W
P+N = 3F
Solving the first equation for N and substituting into the second:
P+W−F = 3F
Resolving for F:
F = (P+W)/4
Answer
F = (P+W)/4
Problem 4
A ladder is standing at some angle to the floor. It's in equilibrium,
that is it's not slipping down to the floor. What holds it is the static friction between it and the floor.
If the ladder stands almost vertically, the static friction is
greater and it easily holds the ladder in the position. As we move the
bottom of a ladder away from the vertical, there will be a point when static friction will no longer could hold the ladder in place and the ladder would slip down to the floor.
What is the smallest angle the ladder would hold if the coefficient of static friction is μ?
Solution
Consider the following illustration to this problem.
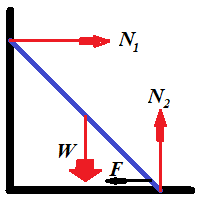
While the reaction of the wall N1 is smaller than the static friction F, the ladder would hold its position.
The smallest angle between the ladder and the floor will be when these two forces are equal.
To be in equilibrium, vector sum of all forces must be equal to
null-vector and a sum of all angular momentums also must be equal to
null-vector.
Along the horizontal X-axis the sum of all forces equals to zero if the horizontal reaction of the wall N1 equals to the force of static friction F, which, in turn, equals to a product of the vertical reaction of the floor N2 by a coefficient of static friction μ:
(a) N1 = μ·N2
Along the vertical Y-axis the sum of forces equals to zero if the reaction of the floor N2 equals to weight of a ladder W:
(b) N2 = W
To analyze angular momentums, let's choose an axis of rotation. It's
easier to choose an axis perpendicular to both X- and Y-axis that goes
through a point where a ladder touches the floor. In this case angular
momentums of forces N2 and F are zero because their corresponding radiuses are zero.
Let's assume that the length of the ladder is D and the angle between the ladder and the floor is φ. The magnitude of the angular momentum of the force of weight W will then be W·D·cos(φ)/2. The magnitude of the angular momentum of the reaction of the wall N1 will be N1·D·sin(φ). The condition of the sum of angular momentums to be equal to zero results in the equation:
N1·D·sin(φ) = W·D·cos(φ)/2
The length of the ladder can be canceled:
(c) N1·sin(φ) = W·cos(φ)/2
Equations (a), (b) and (c) form a system of three equations with three unknowns:
(a) N1 = μ·N2
(b) N2 = W
(c) N1·sin(φ) = W·cos(φ)/2
From this
tan(φ) = 1/(2μ)
Answer
φ = arctan[1/(2μ)]
Interestingly, the answer does not depend on the weight or the length of the ladder.


No comments:
Post a Comment