Unizor - Physics4Teens - Mechanics - Statics - Point-Objects

Notes to a video lecture on http://www.unizor.com



Equilibrium of Point-Objects



The state of equilibrium in a case of possibility of a
point-object to move in some direction implies that the position of this
object does not change, which, in turn, implies that the vector sum of
all forces acting on it is a null-vector:

ΣF_i = 0 .



In three-dimensional world each force F_i
has three components - the projections of this force on X-, Y- and
Z-axis. In order for a sum of vectors to be equal to a null-vector, it
is necessary and sufficient for a sum of their X-components to be equal
to 0, same for Y- and Z-components.

Therefore, we can construct three equations, one for each axis, to determine forces participating in the state of equilibrium:

ΣF_i^(x) = 0

ΣF_i^(y) = 0

ΣF_i^(z) = 0



The fact that only three equations determine the conditions on forces to
be in equilibrium in a three-dimensional world means that unique
determination of these forces is possible only if the number of unknowns
does not exceed three. If four or more unknown variables participate in
the state of equilibrium, we will have infinite number of solution of
the system of three linear equations with four or more unknowns.

Most likely, for our purposes we will consider situations with only unique solutions.



As a simple example of an equilibrium in three-dimensional space,
consider a chandelier of some weight hanging from a ceiling on three
threads attached to a ceiling at three different points. For simplicity,
assume that a chandelier is a point-object and three points of
attachment of the threads to a ceiling are making an equilateral
triangle and the length of all threads is the same.



The weight of a chandelier W is balanced by three equal in magnitude T,
but acting at different angles, tension forces along each thread.
Knowing the weight of a chandelier and an angle of each thread with a
vertical φ (the same for each thread in our simple case), we can easily determine the magnitude of the tension force of each thread:

3·T·cos(φ) = W

T = W / [3·cos(φ)]

Here we only constructed the equation along the vertical Z-axis because
in a horizontal plane (along X- and Y-axis) the tension forces balance
each other.



The example above is a perfect illustration to our next discussion.



Stable Equilibrium



We call an equilibrium stable if, after a small movement of an object from its position of equilibrium, it returns back to this position.



A small push of a chandelier will result in its light swinging and eventual return to the original position of equilibrium.



Consider a cup in a form of semi-sphere and a small ball at the bottom of this cup. It lies in the state of stable equilibrium. If we push it off this position, it will eventually return back because the sum F of reaction force R of the cup and the weight W of a ball always act in a direction of the lowest point of this semi-spherical cup.



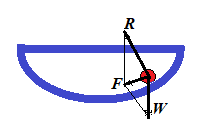
Let's formulate the definition of a stable equilibrium in more precise terms.

For this we have to consider a position of an object in equilibrium and
its immediate neighborhood. Since we consider the equilibrium to be
stable, we have to consider the deviation of an object from a position
of equilibrium.

Basically, we would like to say that the equilibrium is stable, if an
object returns to it from any neighboring point. How big is the
neighborhood, from which this return takes place is, obviously, a
subject of a definition.

The rigorous definition of a stable equilibrium defines the neighborhood as any, however small, one.



So, if exists a real positive value ε such that from any point within ε-neighborhood
of a position of equilibrium an object, placed at this point, returns
to a position of equilibrium, the equilibrium is stable.



Unstable Equilibrium



The unstable equilibrium is the opposite of a stable one. That
means that any, however small, deviation of the object's position from
the position of equilibrium results in moving of this object away from
the equilibrium point.

Obvious example is a small ball on the top of a sphere. If its position
is exactly at the North Pole, it's in equilibrium. But any, however
small, deviation from the NorthPole results in complete departure from
the position of equilibrium.



Neutral Equilibrium



Consider a ball on a horizontal plane. There are two forces acting on it
- gravity vertically down and reaction of the plane vertically up and
equal in magnitude to the ball's weight. These two forces neutralize
each other, no matter where on the plane our ball is positioned. So, any
position is a position of equilibrium. This is exactly what neutral equilibrium is.

Any deviation from the position of neutral equilibrium results in the new equilibrium.

Strictly speaking, neutral equilibrium implies existence of some
neighborhood around the position of equilibrium such as any position
within this neighborhood is a position of equilibrium.



Solids and Six Degrees of Freedom



Before we talked about equilibrium of a point-object, that is a state of
rest, when all forces applied to it are in balance and their sum is
null-vector.

Let's expand our concept of equilibrium to solids. Obviously, they not
only can move in three different directions (forward-backward along
X-axis, left-right along Y-axis, up-down along Z-axis), but also can
rotate around any of the three coordinate axis.

That means that a position of a solid is determined by six parameters - so called six degrees of freedom. Equilibrium of this solid object implies its state of rest along each of these six degrees of freedom.



We know how to deal with the first three degrees of freedom associated with translational motion.

Conditions of equilibrium related to rotation - the other three degrees of freedom - will be analyzed in the next section.