Unizor - Derivatives - Amazing Function Limits

Notes to a video lecture on http://www.unizor.com

Amazing Limits

There are two very important limits that require special attention and non-trivial approach to analyze.
In this lecture we present them with full proof.

Amazing Limit #1

sin(x)/x → 1 as x→0

Proof

We will prove this for angles xin the first quadrant only where x, sin(x) and tan(x) are positive, the general case trivially follows from it. Let's start from the definition of trigonometric functions using the unit circle.

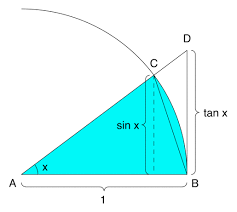
On the picture above sin x segment is an actual definition of a sine. A segment marked tan x is not a direct definition of tangent (defined as a ratio of sine to cosine), but immediately follows from it considering similar triangles ΔADB and ΔACE (point E is a base of a perpendicular from point C to X-axis, not marked on a picture).

Let's compare the areas of three geometric figures:
(a) triangle ΔACB,
(b) circular sector ACB between radiuses AC, AB and arc CB,
(c) triangle ΔADB.
Obviously,
Area(a) ≤ Area(b) ≤ Area(c)
Now let's calculate them all.

Area(a)=AB·sin(x)/2=sin(x)/2
Area(b)=πAB²x/(2π)=x/2
Area(c)=AB·tan(x)/2=tan(x)/2

Therefore,
sin(x) ≤ x ≤ tan(x)
or, since tan(x)=sin(x)/cos(x),
sin(x) ≤ x ≤ sin(x)/cos(x)

Dividing all by positive sin(x), we obtain
1 ≤ x/sin(x) ≤ 1/cos(x)
The left expression is a constant 1, the right expression tends to 1 as x→0 since cos(0)=1. Therefore, by squeeze theorem, the middle expression has a limit as x→0 and its limit is 1:
x/sin(x) → 1 as x→0
Therefore,
sin(x)/x → 1/1=1 as x→0
End of Proof.


Amazing Limit #2

(1+x)^1/x → e as x→0
where e is a fundamental constant in Calculus, approximately equal to 2.71.

Proof

First of all, we have to recall the definition of number e.

There are many definitions of e, all equivalent to each other.
In our course we have chosen the definition of e as a base of an exponential function y=e^x with steepness (which is, actually, a trigonometric tangent of a tangential line) at point x=0 being equal to 1 (that is, the tangential line at x=0 is parallel to a line y=x).

Using the terminology we are now familiar with, the steepness of a curve that represents the graph of a real function y=f(x)or, simply, the steepness of a real function y=f(x) at some point x=r is a limit of the ratio
[f(r+d)−f(r)]/d as d→0.

So, we can say that defining characteristic of number e is lim_x→0[(e^x−1)/x] = 1

Let's approach this from the position of a function graphs.
The graph of a function y = e^x−1 (which is a graph of function y = e^x shifted down by a unit) is going through the origin of coordinates and at this point, according to a definition of a constant e, its tangent coincides with the graph of function y = x.



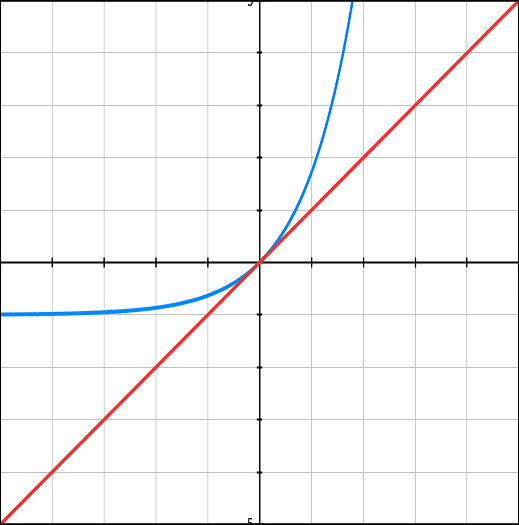
Let's analyze now the meaning of the limit we have to prove.
First of all, let's recall that, if f(x) is a continuous function and x→r, then f(x)→f(r) - this is, actually, a definition of a continuous function.
Next, it can be proven that functions e^x and ln(x) (a natural logarithm - a logarithm with a base e - log_e(x)) are continuous.
Therefore, instead of proving the limit
(1+x)^1/x → e as x→0,
we can prove that
ln(1+x)^1/x → ln(e) as x→0

Simple transformation results in the following formulation of our theorem.
Prove that
ln(1+x)/x → 1 as x→0
Let's draw a graph of ln(1+x)near point x=0 and compare it with a graph of function y=x.



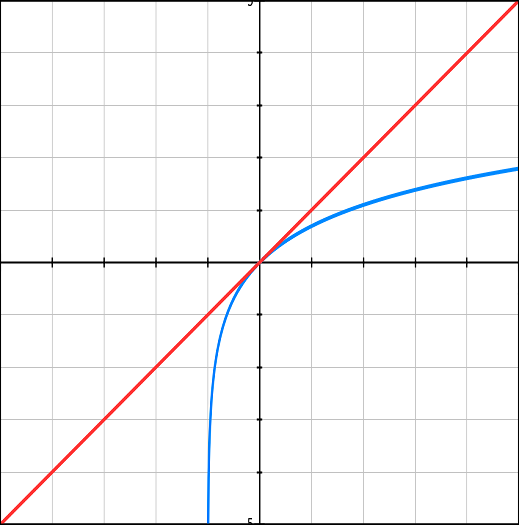
Notice that function y=ln(1+x)is inverse relative to function y=e^x−1. Here is why:
y=e^x−1 ⇒
⇒ y+1=e^x ⇒
⇒ ln(y+1)=x
so, an inverse function is y=ln(1+x).

As we know, an inverse function has a graph symmetrical to the original one relative to an angle bisector of the main coordinate angle.
This implies that, if the line y=xis tangential to a graph of function y=e^x−1 at point x=0 (which is the origin of coordinates because y=e⁰−1=0 as well), the line symmetrical to this tangential line should be tangential to a graph of function y=ln(x+1) at a point symmetrical to the origin of coordinates.

But the tangential line y=x is the angle bisector and is the axis of symmetry, so its symmetrical is itself.
Also, a point symmetrical to the origin of coordinates is itself.
So, we have that the same line y=x is tangential to both y=e^x−1 and y=ln(x+1) at the same point, which proves that
[ln(1+x)−ln(1+0)]/x → 1
as x→0.

We know that ln(1)=0. Therefore, the last expression is simplified into
ln(1+x)/x → 1 as x→0.

This completes the analysis of a problem. We are ready now to prove the original theorem.
Let's start from the last statement that we have proven using the considerations of symmetry between the original function y=e^x−1 and its inverse y=ln(1+x), that is:
ln(1+x)/x → 1 as x→0.
Let's transform it into an equivalent form using the property of logarithm log(a^b)=b·log(a) into the following:
ln((1+x)^1/x) → 1 as x→0.
Using continuity of a function e^x, apply it to the above statement:
(1+x)^1/x → e¹ as x→0.
Since e¹=e, we have the original statement proven:
(1+x)^1/x → e as x→0.
End of proof.

A simple consequence of this limit is that
(1+1/n)ⁿ → e as n→∞
since 1/n → 0 as n→∞