Notes to a video lecture on http://www.unizor.com
Magnetism of Straight Line Current
Magnetic properties of permanent magnets are attributed to parallel
orientation of all axes of rotation of electrons around corresponding
nuclei and the same direction of this rotation.
Consider an Ampere model of magnetism that we have addressed in one of
the previous lectures and, in particular, all electrons rotating in the
same plane.
If all electrons rotate in the same direction within the same plane
around parallel axes, electrons moving near each other are moving in
opposite directions and neutralize each other, as if there is no current
there at all.

So, within every plane perpendicular to the North-South axis of a magnet
all inner currents are neutralized, and the only really present current
is around the outer boundary of a magnet.
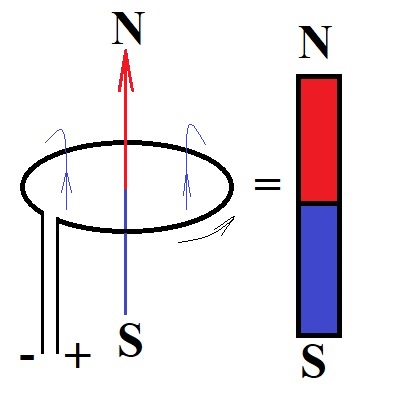
This makes the magnetic properties of permanent magnet equivalent to
properties of an electric current in a loop. The flow of electrons,
constituting this electric current, occurs within one plane with a
perpendicular to this plane making the North-South line of this
artificially made magnet.
Simple experiment with iron filings confirms the similarities of
magnetic properties of permanent magnet and a loop of wire with electric
current running through it.

In the previous lectures we described the Lorentz force that acts on the
electric current in the magnetic field of a permanent magnet. Now we
will use the electric current as the source of the magnetic field and
will talk about the properties of this magnetic field in relation to
electric characteristics of the current.
First of all, we will switch from an electric current in a loop to a straight line current.
Consider the magnetic field lines around the wire carrying the electric
current in a loop. Inside a loop they go in the direction from the South
pole towards the North along the axis, then circle around the wire from
the North pole back to the South.
The round shape of a wire causes the polarization of the magnetic field.
Polarity is determined by the high density of the magnetic field lines
inside the loop, all pointing to the North, while the opposite direction
of the lines outside the wire loop is less dense, representing a weaker
magnetic field.
Now let's open up a loop into a straight line electric current.
Magnetic field will not disappear and magnetic field lines will still go
around the wire that carries an electric current, just more
symmetrically than in case of a wire in a loop.
Simple experiment with iron filings confirms the circular shape of
magnetic field lines around a straight line wire carrying an electric
current.
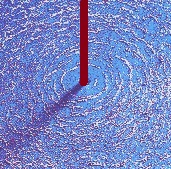
The following picture represents a straight line wire carrying the electric current and magnetic field lines around it.
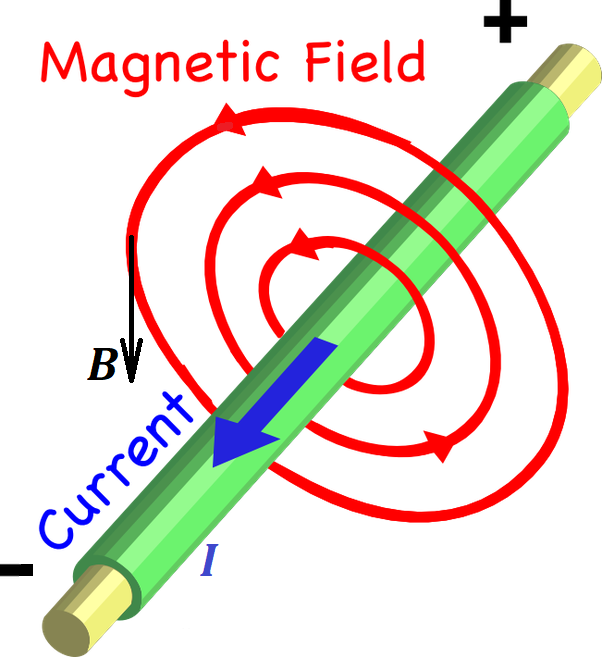
The current in the wire causes the magnetic field to be formed around it.
The magnetic field lines are now completely symmetrical relative to the
wire, thus the magnetic field has no polarity. All lines are perfectly
circular, each forms a circle of certain radius around a wire, lying in
the plane perpendicular to the wire and representing the points of the
same strength of the intensity vector of the magnetic field.
Let's assume that our wire is ideally straight, infinitely long, and infinitesimally thin.
Our task is to relate the electric current running through it with the intensity of the magnetic field B around it at distance R from the wire.
The intensity of the magnetic field B is a vector, whose
magnitude we want to determine. The direction of this vector is always
tangential to the circular magnetic line lying in the plane
perpendicular to the wire and going through a point where we want to
measure this magnetic field intensity and, therefore, always
perpendicular to the wire.
From considerations of symmetry, the distance R should be
the only variable needed to characterize a point in space around the
wire, where we want to determine the intensity of the magnetic field.
Since the magnetism of an electric current running through a straight
wire depends on existence of the current in a wire, it's reasonable to
assume that the more electrons participate in the current (that is, the
greater amount of electricity goes through a wire per unit of time, that
is, the greater amperage of an electric current I) - the stronger magnetic effect it causes. So, the intensity of a magnetic field B around a wire with electric current I running through it should be proportional to the amperage of the electric current in a wire:
B ∝ I
If we consider a field, including a magnetic field, as some form of
energy, emitting by a source of this field and spreading into space all
around this source with certain speed, at any given moment of time it
reaches new "frontier" and spreads over this surface of equal timing
(this is not a generally used terminology, but is appropriate to better
understand the concept of a field). Obviously, the farther we are from a
source - the greater "frontier" area is covered by a field and less of a
field energy falls on a unit of area of this surface.
Hence, the field intensity, which can be viewed as amount of energy
falling on a unit of area per unit of time should diminish as the
distance from the source of a field is increasing because the area of a
surface of equal timing increases with time.
These considerations were a basis for deriving the intensity of an
electrostatic field of a point charge as being inversely proportional to
a square of a distance from this point charge and related to the fact
that all points at a distance R from a source of a filed form a sphere and the area of a sphere of radius R around a source of a field is 4πR².
The same amount of energy going through a sphere of one radius goes
through a sphere of a radius twice as big and, therefore, "covers" the
area four times bigger.
Let's examine the magnetic field of a straight line current using the same logic.
In this case the field source is a straight line. All points on the same
distance from it form a cylinder. The side area of a cylinder of a
radius R and height H is 2πR·H, that is proportional to a radius R.
The height is not important in our case since we assumed that the wire
carrying the electric current is infinite, but the factor 2πR must be in the denominator of a the formula for intensity of a magnetic field of a straight line electric current.
So, we have logically came to a conclusion of proportionality of the
intensity of a magnetic field to the amperage of the current and inverse
proportionality to the distance from the wire:
B ∝ I/(2πR)
Coefficient of proportionality in this formula is called the permeability of free space and is denoted μ0. So, the final formula for intensity of a magnetic field of a straight wire carrying electric current I at a distance R from a wire is:
B = μ0I/(2πR)
The value of the permeability of free space constant depends on the
units of measurement and in SI units, according to the above formula,
it's supposed to be measured in
T·m/A = N·m/(A·m·A) = N/A²
Its value is, approximately,
μ0 ≅ 4π·10−7 N/A²


No comments:
Post a Comment