Notes to a video lecture on http://www.unizor.com
Capacitors
Electric Field of
a Uniformly Charged Disk
Please refer to Problems 4 of "Electric Field", as we will use its results.
The problem there derives a formula of intensity of the electric field produced by an infinitely thin disk of radius R charged with surface density of electricity σ at point P positioned at height h above the center of this disk in case the space around this disk is filled with material with dielectric constant (also known as relative permittivity) εr.
The direction of the vector of electric field intensity is along the perpendicular from point P to a charged disk and its magnitude equals to
E(h) =
= [σ/(2εr·ε0)]·[1−1/√1+R²/h² ]
From the above formula for any media filling the space around a charged disk we see that the greater dielectric constant εr for the media that fills the space around the charged disk - the smaller intensity of the field around it.
Assume now that our goal is to generate electric charge (excess or deficiency of electrons) and store it somehow. Since electrons are not easily produced from nothing, we should take some electrically neutral object X, separate part of its electrons from the atoms and place them into a different object X−, which becomes negatively charged, leaving old object positively charged, which we can label now X+.
For practical reasons objects X− and X+ should be near each other and we should prevent any kind of exchange of electric charge, like a spark, between them, which would negate our efforts to separate negative and positive charges. Considering the proximity of X− and X+, it would be beneficial for avoiding any exchange of the charge between them to have a uniform distribution of charge in each object.
The best configuration of objects X− and X+ that allows approximately uniform distribution of charge in the presence of opposite charge nearby is when both objects are thin flat plates positioned parallel to each other. Other configurations will cause the concentration of charges in places close to the opposite charge and higher intensity of the electric field between them, which might result in a discharging spark. Another configuration might be of two concentric spheres, but it's not very practical.
Consider now two relatively large infinitely thin disks of radius R with opposite charges +Q and −Q positioned parallel to each other, perpendicular to a line connecting their centers and at distance d from each other. Let's measure an intensity of the electric field at any point between these disks on a center line at distance h from positively charged disk
The intensity of a combined field of two disks is a vector sum of intensities of all components of this field. The direction of the intensity of both fields is along the center line between them. The probe charge is +1C, so the positively charged disk will repel it, while negatively charged one will attract it. So, we can calculate the magnitude of each field and add them together to get the magnitude of the combined field.
The density of the electric charge for these disks equals to a total charge Q divided by a surface area A. There are two opposite surfaces of each disk, but in case we have two close to each other parallel disks with opposite charges the electric charge of each disk (excess or deficiency of electrons) concentrates on a surface that is close to another disk with an opposite charge. So for each disk the absolute value of charge density is constant that equals to
σ = Q/A = Q/(πR²)
The magnitude of the field intensity from a positively charged disk at distance h from its surface is
E(h) =
= [σ/(2εr·ε0)]·[1−1/√1+R²/h² ]
The magnitude of the field intensity from a negatively charged disk at distance d−h from its surface is E(d−h).
Just as an observation, let's notice that, in case the disks are very large and the distance between them very small, both E(h) and E(d−h) are approximately equal to
E = σ/(2εr·ε0)
Since both vectors of intensity are directed from positive to negative disk (positively charged disk repels the probe charge of +1C positioned in-between the disks, and the negatively charged disk attracts it), the magnitude of the intensity of the combined electric field produced by both disks equals to
E(h) = E(h)+E(d−h)
Expressed in all its details, the formula is quite large and difficult to analyze.
At this point we will do what physicists usually do with a cumbersome formula - assume that in practice certain really small values can be assumed as infinitely small and certain large values to be infinitely large.
Indeed, if h→0 or h→d the assumption above is correct. Representing graphically intensity E as a function of h for R=10 and d=0.1 on a segment
So, for practical reasons we will assume that the distance between the disks d is very small, while the radius of disks R is very large. Since the point we measure the intensity is between the disks at the distance h from one of them, variables h and d−h can also be assumed as very small.
This assumption leads to consider the values R²/h² and R²/(d−h)² as infinitely large, which result in the following approximate formula for the intensity of a combined field between the disks:
E ≅ σ/(2εr·ε0) + σ/(2εr·ε0) =
= σ/(εr·ε0)
So, approximately, the electric field between the large parallel disks on a small distance from each other is uniform and depends only on the density of electric charge on the disks σ and the dielectric constant of the media between them εr.
Let's analyze a process of discharging of electricity between two disks.
Since our purpose is to store the charges and to avoid discharge, we should know how much electricity Q we can store in these two disks before electrons jump from a negatively charged disk to a positively charged because of the force of attraction.
The discharge will be more difficult if the force of attraction between the disks is less. The force of attraction is characterized by the intensity of the field between the disks. Knowing intensity of the field between the disks E, which is the force acting on a unit charge, we can calculate the work needed by a charge of +1C to overcome a distance d between the disks by multiplying the intensity (force) by the distance.
The work needed to discharge +1C, that is the work needed to move +1C of charge from one disk to another (the voltage between the disks) is
V = E·d = σ·d/(εr·ε0)
Let's recall that the purpose of our work is to store as much electric charge in these two disks as possible. But with growing charge Q proportionally grows the density of electricity σ and proportionally grows the intensity of the field and the voltage between the disks.
Let's introduce the new characteristic that defines the ability of our two disk construction, called capacitor, to hold electric charge - capacity C = Q/V.
Defined as such, the capacity of a capacitor described above equals to
C = Q/V = σ·A/[σ·d/(εr·ε0)] =
= A·(εr·ε0)/d
As we see, the capacity of our capacitor depends on three major factors:
(a) the area of the disks (capacity is proportional to this area)
(b) the distance between disks (capacity is inversely proportional to this area)
(c) the dielectric constant of the media between the disks (capacity is proportional to a dielectric constant of the media).
To satisfy the purpose of storing as much electricity in the capacitor as possible, we should increase the area of the disks, decrease the distance between the disks and isolate disks from each other with the media with high dielectric constant.
The disk shape of a capacitor is not really important, as long as it contains two flat parallel shapes on a small distance from each other. The easiest variation from the practical standpoint is two rectangles. Although different shape leads to slightly different results in the value of capacity, the difference is negligible, and it disappears completely when the distance between planes becomes an infinitesimal value. So, the definition of capacity
C = A·(εr·ε0)/d
is quite universal and is widely used as a characteristic of a capacitor.
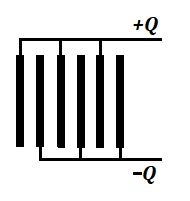
Finally, if we adapt a rectangular form of a capacitor, it's easy to significantly increase the area A by folding or rolling both surfaces together. This technique is actually utilized in manufacturing capacitors of large capacity and it's called parallel connection of capacitors.
In such a way of connecting capacitors the total capacity of an assembly equals to a sum of capacities of individual capacitors
C = C1+C2+C3+C4+...
This picture depicts an idea to stack smaller individual capacitors to enlarge the area, thus allowing to store more electric charge in a smaller volume.


No comments:
Post a Comment