Unizor - Physics4Teens - Mechanics - Dynamics - Superposition of Forces ...

Notes to a video lecture on http://www.unizor.com



Motion on Inclined Plane



Problem A



Consider a slope fixed on the ground that makes an angle φ
with horizon. Let's analyze the motion of an object, as it slides down a
slope under its own weight. Our task is to determine its acceleration
along the slope.



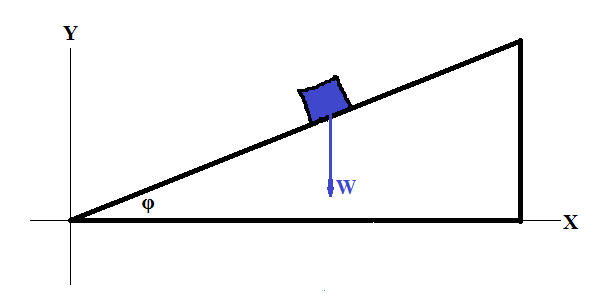
First of all, we have to choose a reference frame - a system of coordinates suitable for this problem.

The main force acting on this object is its weight W - a vector of gravity
directed vertically down to the ground. That prompts us to choose a
frame of reference with horizontal X-axis and vertical Y-axis. So, the
vector of weight has non-zero Y-component and zero X-component: W = {0,W}, where W is a magnitude of vector of weight W. However, this obvious choice is not the best in a case like this.



There are usually numerous forces involved in an experiment and only few
objects. In this case there is only one object. So, instead of catering
to one particular force, like weight, it's better to simplify the motion of a single object.

Much more convenient frame of reference would be the one, where our object in motion has only one non-zero coordinate.



Recall that there must be another force acting on an object - reaction force of the slope, that prevents an object to go vertically down to the ground through a slope and forces it, in cooperation with gravity force, to slide along a slope. This reaction force R
is always perpendicular to the surface, where an object is on (in this
case, perpendicular to a slope), and its magnitude is such that the resultant of the weight W and reaction R is directed along a slope.



Consider a frame of reference with X-axis going along the slope, where the object slides down and Y-axis perpendicular to it.



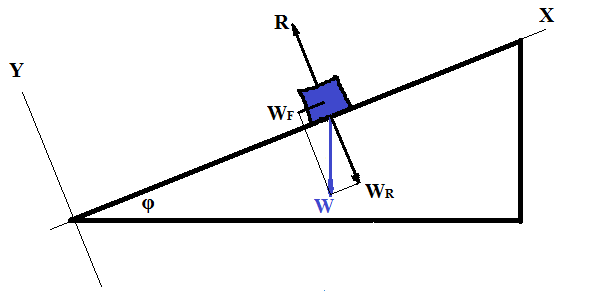
Granted, the weight now has both coordinates non-zero:

(a) perpendicular to a surface of a slope and (on the picture above) directed along negative Y-coordinates vector W_R with magnitude W_R=W·cos(φ), that causes reaction force R, that is equal in magnitude and opposite in direction to W_R, and

(b) parallel to a slope, directed (on the picture) towards negative X-coordinate, vector W_F with magnitude W_F=W·sin(φ), that is the cause of motion of our object down a slope.



As it is pictured, both components of weight are negative since they are
directed towards negative direction of the X- and Y-axes:

W = {−W·sin(φ),−W·cos(φ)}

Force R , as opposite and equal in magnitude to W_R, is

R = {0,W·cos(φ)}.



The resultant of three vectors W_R, W_F and R is W_F, directed down a slope, equaled in magnitude to W·sin(φ).



Therefore, an object of mass M will slide down a slope with acceleration equaled in magnitude to

a = W_F/M = W·cos(φ)/M

Since weight and mass of an object are related as W=M·g, where g is a known acceleration of free falling (9.8 m/sec² on the Earth ground), the resulting acceleration equals in magnitude to

a = M·g·sin(φ)/M = g·sin(φ)

In vector form in the chosen reference frame:

a = {−g·sin(φ), 0}





Problem B



Consider an object A of mass m, sliding without friction
on a slope of slide B, which itself lies on a horizontal surface and can
slide on it without friction. An angle of a slope of slide B is φ with horizon, its mass is M.

Our task is to determine acceleration a of slide B.

Let's analyze the motion of object A on a slope and the motion of a
slide B, as it moves horizontally, as a result of the weight of object A
on it.





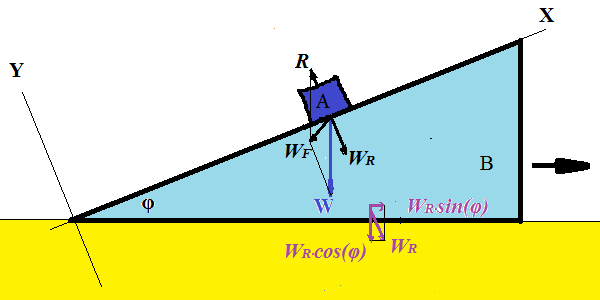
As object A presses down with its weight, it slides downhill along a
slope of a slide B. At the same time slide B moves to the right (on the
picture above).

The horizontal component of the pressure W_R of
an object A on slide B perpendicularly to its slope is the cause of the
motion of a slide B. However, this pressure is not the same as in the
problem A above. It will be less. Its opposite reaction force R, that is equal in magnitude to W_R, but acting on the object A, will also be less than in the problem A above.

The resultant of weight W and reaction force R is force W_F that is not parallel to a slope, but tilted downwards.

So, the combination of object A sliding downhill on a slope and slide B
movement to the right produces the resultant move of object A that is
not parallel to a slope, neither it is directed vertically down, but
will be somewhere in-between.



Let's consider the same reference frame as in the problem A above. Now
both object A and slide B, as they move, have both X- and Y-components
not equal to zero.



Consider only Y-coordinate of the A object now and Y-components of forces acting on it.

In the direction of Y-axis the force W_F = W + R, acting against object A, has value

W_Fy = W_y + R_y = R − W·cos(φ)



This force R − W·cos(φ), according to the Newton's Second Law, should be equal to object A's mass m, multiplied by a Y-component of its acceleration, which so far is unknown.



Let a be an acceleration of slide B in the direction of
its horizontal movement. Since displacement of object A in the direction
of the Y-axis (perpendicularly to a slope) equals to horizontal
displacement of a slide B multiplied by sin(φ), the
acceleration of slide B in the horizontal direction and acceleration of
the object A in a direction perpendicular to a slope, maintain the same
factor.

Therefore, the acceleration of object A perpendicularly to a slope of slide B equals to a·sin(φ), where a is the acceleration of the slide B that we have to determine in this problem.



The Newton's Second Law for object A in the direction of the Y-axis (perpendicular to a slope of slide B) is

R − W·cos(φ) = −m·a·sin(φ)

(minus on the right because the acceleration of object A relative to Y-axis is negative).

This equation is the first in a system of two equations that include two unknowns R and a.



On the other hand, a horizontal component of vector −R is the cause of horizontal acceleration a of slide B that has mass M.

Therefore,

R·sin(φ) = M·a

This is the second equation in a system of two equations that include two unknowns R and a.



Solving this system as follows.

From the second equation:

R = M·a/sin(φ)

Substitute it in the first equation:

M·a/sin(φ) − W·cos(φ) =

= −a·m·sin(φ)



The solution for horizontal acceleration of slide B is

a = W·cos(φ) /

/ [m·sin(φ) + M/sin(φ)] =

= W·sin(φ)·cos(φ) /

/ [m·sin²(φ)+M]



So, our final result for an acceleration a of slide B, as it moves horizontally, is
W·sin(φ)·cos(φ)/[m·sin²(φ)+M]