Notes to a video lecture on http://www.unizor.com
Superposition of Forces -
Problems 2
Problem A
Consider a slope that makes an angle θ with the ground. On
the top of this slope there is a pulley, through which goes a
weightless non-stretchable thread that connects two point-objects:
one of mass M1, sliding up the slope, and
another of a bigger mass M2, hanging off the top pulley vertically down and pulling the thread down, thus forcing the smaller object to go up the slope.
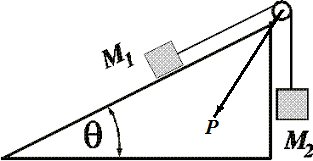
Determine the direction and magnitude of the pressure vector P on the pulley's axis.
Answer:
Direction of the vector of pressure on the pulley's axis P is along the angle bisector of the angle at the top of a pulley.
The magnitude of this vector is
P = k·[1+sin(θ)]·cos(π/4−θ/2)
where
k = 2M1·M2·g / (M1+M2)
Problem B
A point-object is hanging on a thread of length L and is uniformly moving along a circular trajectory in a horizontal plane, while a thread always maintains a constant angle φ with a vertical.
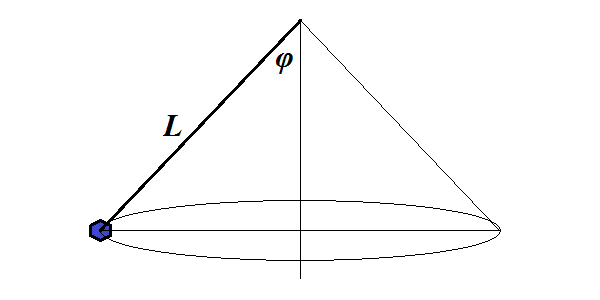
How many loops N(t) this object does in time t?
Answer:
N(t) = (t/2π)·√g/[L·cos(φ)]
where g is a free fall acceleration.
Problem C
A wedge of mass m and angle 2φ slides down between two point-objects of mass M each, pushing them apart without any friction.
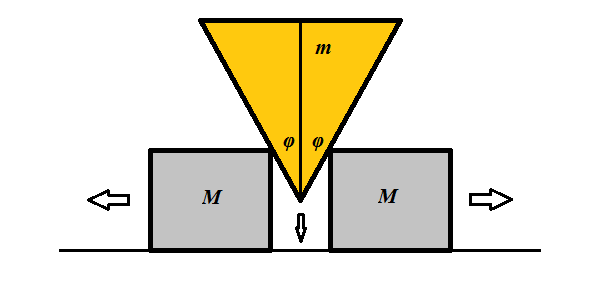
Find the acceleration a of each of the two objects that a wedge pushes apart.
Answer:
a = g·tan(φ)/
/[1+2(M/m)·tan²(φ)]
Problem D
During long jump competition a sportsman accelerates with constant acceleration a during time t and then jumps vertically up.
During his jump he goes up to height h, while continuing moving forward because of his initial horizontal speed he gained before jumping.
What is the length L of his jump?
Answer:
L = 2a·t·√2h/g


No comments:
Post a Comment