Unizor - Physics - Mechanics - Kinematics - Frames of Reference - Proble...

Notes to a video lecture on http://www.unizor.com



Kinematics Problems 2



Problem 1

A gear consists of two toothed wheels connected to each other as on this picture:


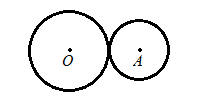
The size of the teeth is negligible relative to the size of the wheels.

A bigger wheel rotates around fixed point O, has radius R and angular speed ω.

A smaller wheel rotates around fixed point A and has radius r.

Wheels are locked by their teeth, so the rotation of a bigger wheel forces the rotation of a smaller one.

What is the angular speed of rotation of a smaller wheel?



Answer:

R·ω/r





Problem 2

Assume a frame of reference with Z-axis along the Earth's axis and
XY-plane containing an equator, but fixed relative to stars, so the
Earth rotates in this frame around Z-axis.

Also assume that the Earth is an ideal sphere of a radius R=6400 km and it makes one rotation around its axis in exactly T=24 hours.

What is a magnitude v of a vector of velocity (linear speed) of a point on the surface of the Earth on the latitude of φ=60°?



Answer:

v = 2πR·cos(φ)/T ≅

≅ 838 km/hour ≅ 233 m/sec.





Problem 3

Assume a frame of reference is attached to the Earth with Z-axis along the Earth's axis and XY-plane containing an equator.

Also assume that the Earth is an ideal sphere of a radius R=6400 km and it makes one rotation around its axis in exactly T=24 hours.

A plane flies at altitude H=10,000 m above the surface of the Earth from East to West above the same latitude with a linear speed v=900 km/hour.

A passenger who always looks through a window sees the Sun at exactly the same position all the time.

What is the latitude φ, above which the plane is flying?



Answer:

cos(φ) = (v·T)/[2π·(R+H)] ≅

≅ 0.536310

φ ≅ 1.00473725 rad ≅

≅ 57.5672°.





Problem 4

Two hands on the clock coincide at noon.

How long will it take for them to coincide again?



Answer:

12/11 hour.





Problem 5

A river flows along a straight line with constant flow with both banks parallel to each other. The width of a river is S.

A boat goes from one river bank to another, maintaining a course
perpendicular to a river, with a speed twice the speed of the river
flow.

How far down the river the flow will take the boat from a point directly opposite to a starting point of a boat?



Answer:

S/2.





Problem 6

There are two cars on XY-plane with Cartesian coordinates.

Car #1 at moment t=0 is at position (A,0) on the X-axis, where A > 0, while car #2 at this moment is at (0,B) on the Y-axis, where B > 0.

Both cars go along their respective axes towards the origin of coordinates with speeds u for car #1 and v for car #2.

At what moment in time t_min the distance between the cars will be minimal?



Answer:

t_min = (A·u + B·v)/(u² + v²).