Notes to a video lecture on http://www.unizor.com
Resultant Force
According to the Principle of Superposition of Forces, we can replace actions of many forces acting upon a point-object (each one being a vector) with a vector sum of these forces (called resultant force), getting exactly the same effect on the motion of a point-object.
An immediate consequence from the Principle of Superposition of Forces
is that any single force acting upon a point-object can be replaced by a
vector sum of a few forces, which produce exactly the same effect on
the motion of a point-object, as long as this vector sum of forces
exactly equals to the vector of original force.
We will demonstrate this Principle on a few examples.
Example 1
In the frame of reference associated with the ground we have a point-object sliding down a slope.
Given are: mass of an object m, force of gravitation of this object (its weight, directed vertically down) W and an angle φ between a slope of a slide and horizontal ground.
Our task is to determine the acceleration of this object on its
trajectory down a slope, considering there is no friction that slows
down the object's movement down a slope.
Solution
Trajectory of our object is a straight line (the slope), mass m
is known, so all we need to find the acceleration from the Newton's
Second Law is the force that pushes this object along its trajectory
down a slope.
Obviously, the slope's angle φ plays an important role here. Consider a slope with φ=0, that is the "slope" is not really a slope, but a horizontal plane. The object will not move then because its weight W, directed vertically down perpendicularly to a horizontal plane, is completely balanced by the reaction force of the plane R
directed vertically up and equal in magnitude to the weight, according
to the Newton's Third Law. The resultant force is zero-vector and there
is no acceleration.
On the other extreme, if our slide is vertical with φ=90°, an object does not press on it, there is no reaction force, all the object's weight W is directed along the vertical trajectory downward, and the acceleration can be determined from the Newton's Second Law as a=W/m.
To meaningfully include the slope's angle φ into our calculation, we will represent its weight W as a vector sum of two forces:
(a) the force WR, directed perpendicularly to a slope, causing slope's reaction force R to balance it, and
(b) the force WF, directed parallel to a slope, pushing the object forward along its trajectory and causing its acceleration.
If we succeed in such representation, we will say that the force WF is the one and only force that pushes the object of mass m down a slope and can be used to determine the object's acceleration from the Newton's Second Law as a=WF/m.
This representation of the weight of an object as a sum of two vectors W=WR+WF, knowing the angle φ, is easy.
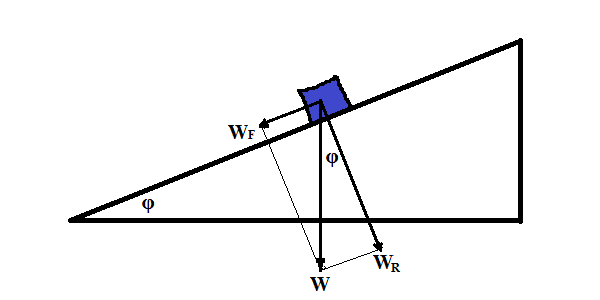
The magnitude of vectors WR and WF, which we will denote as WR and WF correspondingly, equal to
WR = W·cos(φ)
WF = W·sin(φ)
where W is the magnitude of a vector of weight W.
The force WR
is completely balanced by the reaction force of the slope (they both
are perpendicular to a slope, equal in magnitude and oppositely
directed, according to the Newton's Third Law).
So, the only force affecting the motion of an object on its trajectory down a slope and acting along this trajectory is WF, the magnitude of which we have calculated above.
Therefore, an acceleration of an object down a slope will be a vector directed parallel to a slope with a magnitude
a=W·sin(φ)/m.
Example 2
A motorcycle stuntman decides to demonstrate his skills by going inside a vertical loop.
His mass is m.
His linear speed inside this loop is v.
The magnitude of the gravity force (his weight with a motorcycle) is W.
The radius of a loop is R.
Find the pressure on the loop at its top and at its bottom from a moving motorcycle.
Solution
Let's set our frame of reference on the ground with Z-axis directed upward and a loop being in the XZ-plane.
Since an object of mass m moves with a constant linear speed v along a circular trajectory of radius R,
there is a force that keeps it on this trajectory. This force is always
directed towards the center of a circle and is equal in magnitude to m·a, where a is a magnitude of its acceleration towards a center of a circle called centripetal acceleration.
From the Kinematics of rotation we know that a=R·ω², where ω is the angular speed of rotation and is related to linear speed of rotation v as v=R·ω.
From this we derive the centripetal acceleration a in terms of linear speed and radius: a=v²/R.
Knowing the force that keeps an object on a circular trajectory, let's analyze what is the source of this force.
On one hand, there is always a weight directed downward (towards negative direction of Z-axis) and equal in magnitude to W.
On the other hand, an object presses onto the loop with the force P(t)
perpendicularly to the loop, and the loop reacts back unto object with
the same by magnitude but oppositely directed reaction force. This
reaction force is directed upward, when the object is at the bottom of
the loop (we will denote its magnitude as Pb), or downward, when an object is at the top (we will denote its magnitude as Pt).
The combination of weight and the reaction force of the loop is the
resultant force that keeps the object on its circular trajectory.
Therefore, at the bottom of the loop, when weight is directed downward,
reaction is directed upward and the centripetal force is directed
upward,
−W+Pb = m·R·ω²
At the top of the loop, when weight is directed downward, reaction is
directed downward and the centripetal force is directed downward,
−W−Pt = −m·R·ω²
From the first equation we can derive the reaction force at the bottom
that is, by magnitude, equals to the pressure on a loop at this point:
Pb = m·R·ω² + W
From the second equation we can derive the reaction force at the top
that is, by magnitude, equals to the pressure on a loop at this point:
Pt = m·R·ω² − W
Theory of gravitation, that will be studied later in this course, states
that weight is a force of gravity proportional to a product of masses
of a planet and an object on its surface and inversely proportional to a
square of a distance between centers of mass. The latter is
approximately equal to a radius of a planet.
For Earth it is expressed as
On Jupiter, by the way, this constant - free fall acceleration - is equal to
Using this, we can write our formulas for pressure as follows:
Pb = m·R·ω² + m·g = m·(R·ω² + g)
Pt = m·R·ω² − m·g = m·(R·ω² − g)
It should be noted that, while Pb is always positive, Pt
might be negative, if the speed of an object is not sufficient. If
negative, the movement will not be circular and object will fall down
from its trajectory.
If R·ω²=g or ω=√g/R, or v=√g·R,
the object will experience weightlessness at the top position, since it
will not press onto loop and, therefore, loop will not press on it. For
loop of, say, 10 meters in diameter
will produce an effect of weightlessness at the top of a loop. This
linear speed with a given radius of a loop is equivalent to the angular
speed of
Slower speed will result in falling from the circular trajectory.


No comments:
Post a Comment