Unizor - Derivatives - Tangential to a Curve

Derivatives - Tangential to Curve

We have defined a derivative as a speed of change of function value relative to a change in its argument.
In this lecture we will interpret this concept of derivative geometrically.
Our purpose is to draw a tangential line to a curve that represents a graph of function f(x).

Let's assume that we have a function f(x) defined on some interval (a,b). Point x₀ is inside this interval, that is x₀∈(a,b). We have to construct a line tangential to a graph of our function f(x) at point x₀.

Since tangential line is supposed to have one common point with a curve at a point of tangency (x₀,f(x₀), we already have one point our tangential line is supposed to pass through. We need a second parameter to define the tangential line. It can be another point it passes through or an angle it forms with another line. The latter method is preferable and that other line is the X-axis.

To determine the angle our tangential line forms with the X-axis, choose a point x₁ within the same interval (a,b) close to point x₀ and consider a triangle ΔABC on the picture below.



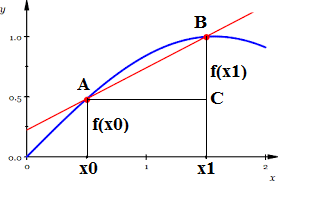
Our plan is to move point x₁ closer to x₀, which will cause point B to move closer to point A and, therefore, line AB to be closer to a tangential line to a curve at point A.

At any moment of this process we know the tangent of an angle ∠BAC:
tan ∠BAC = BC/AC = [f(x₁)−f(x₀)] / (x₁−x₀)

All we have to do now is to take a limit of this expression as point x₁ tends to x₀. If this limit exists (which for some functions f(x) might not be the case), it will be a tangent of a tangential line to our curve at point A - a second parameter needed to completely define the position of a tangential line at this point.

Traditionally, this is expressed using a substitution
x₁ = x₀ + Δx
that results in the following expression for tangent of an angle φ formed by a tangential line at point x₀ with the X-axis:
tan ∠φ = lim_Δx→0[f(x₀+Δx)−f(x₀)]/Δx

As we see, this is exactly the definition of a derivative of a function f(x) at point x₀.
Thus, we came to a geometrical interpretation of a derivative - a tangent of an angle formed by a tangential line to a graph of this function with the X-axis.