Unizor - Derivatives - Parametric Curves

Notes to a video lecture on http://www.unizor.com

Differentiation
of Parametric Curves

Let's assume that we deal with some curve on the plane that is defined not as a graph of certain function that looks like y=f(x)(where x is abscissa and y - ordinate), but parametrically, where both coordinates are defined as functions of some parameter t.
An obvious example is a point moving on a plane, and its position {x;y} depends on a time parameter, so it can be described as {x(t);y(t)}, where both functions x(t) and y(t) are given and differentiable.
So, one independent parameter t describes both coordinates through these two function.

Our task is to find an equation that describes the tangential line to this curve at some point{x₀;y₀} that corresponds to a parameter value t=t₀, that is x₀=x(t₀) and y₀=y(t₀).

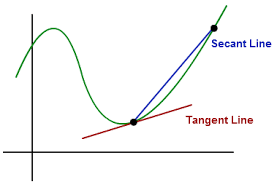
Geometrically speaking, a tangential line to a sufficiently smooth curve at some point is a limit of a secant line that intersects our curve at point where a tangential line should be and another point close to it, when that other point is getting closer and closer to the point of tangency.



Generally, a straight line that goes through point {x₀;y₀} has a point-slope equation
y−y₀ = m·(x−x₀)
So, all we have to determine in the equation for a tangential line that goes through point{x₀;y₀} is its slope m.

Since our tangential line is a limit of a secant, we can assume that the slope of a tangential line is the limit of a slope of a secant as the other point of secant's intersection with our curve is getting infinitesimally close to point {x₀;y₀}.

Consider a point of tangency{x₀=x(t₀);y₀=y(t₀)} and give an increment to parameter t from its value t₀ to value t₀+Δt.
The new point on a curve that corresponds to an incremented value of parameter t will be
{x₁=x(t₀+Δt);y₁=y(t₀+Δt)}

A secant that intersects our curve at points {x₀;y₀} and{x₁;y₁} has a slope equal to
m = (y₁−y₀)/(x₁−x₀)
which can be transformed into
m = Δy/Δx
where Δy=y(t₀+Δt)−y(t₀)
and Δx=x(t₀+Δt)−x(t₀)

Obviously, we want to express the limit of this expression for slope m as Δt→0 in terms of derivatives D_t[x(t)] and D_t[y(t)].
For this we can transform it into
m = (Δy/Δt)/(Δx/Δt)
from which follows that for Δt→0
m→m₀=D_t=t0[y(t)] /D_t=t0[x(t)]
where derivatives are taken at point t=t₀.

Example

A unit circle with a center at the origin of coordinates can be described parametrically with an angle θ from the positive direction of the X-axis to a radius to a point on a circle being a parameter. Let's use the radian measure of this angle.

Any point on a circle with coordinates {x;y} can be described through functions:
x=cos(θ),
y=sin(θ).

Let's choose a point that corresponds to a parameter value θ=π/4 and determine the equation of a tangential line at this point.
First of all, determine the coordinates of a point of tangency:
x=cos(π/4)=√2/2
y=sin(π/4)=√2/2
Now the slope should be equal to a ratio of derivatives of functions y(θ) and x(θ) at point with parameter θ=π/4:
D_θ=π/4[y(θ)]=D_θ=π/4[sin(θ)]=
= cos(π/4) = √2/2
D_θ=π/4[x(θ)]=D_θ=π/4[cos(θ)]=
= −sin(π/4) = −√2/2

The slope m of our tangential line is a ratio of the two values above:
m = (√2/2)/(−√2/2) = −1

So, the equation of our tangential line at point defined by parameter θ=π/4 in point-slope form is
y−√2/2 = −1·(x−√2/2)
or, in a standard form,
y = −x + √2