Unizor - Derivatives - Concept of Differential

Notes to a video lecture on http://www.unizor.com

Concept of Differential

A concept of differential of a smooth function f(x) at point x=x₀ was briefly introduced when we defined a derivative of a function as a linear function of an infinitesimal increment of its argument with a coefficient of proportionality equal to a derivative of this function at point x=x₀.

The notation df(x₀)/dx=f ^I(x₀), which was introduced when we defined a concept of derivative, reflects this definition.
Here x₀ is any point in the domain of function f(x), dx is an infinitesimal increment of argument x from this point and df(x₀) is differential of function f(x) introduced above.

The notation that uses d instead of Δ implies that we are not talking about just any particular increment, but about a process of decreasing this increment to zero, thus making it an infinitesimal variable.

Using this type of notation, we can write the definition of a derivative as follows:
f ^I(x₀) =
= lim_dx→0[f(x₀+dx)−f(x₀)]/dx
This implies that
[f(x₀+dx)−f(x₀)]/dx = f ^I(x₀)+ε
where ε is another infinitesimal variable.
Next transformation:
f(x₀+dx)−f(x₀) =
= f ^I(x₀)·dx+ε·dx
or, using the definition of "littleo" as infinitesimal of higher order,
Δf(x₀) = f(x₀+Δx)−f(x₀) =
= f ^I(x₀)·dx+o(dx) =
= df(x₀) + o(dx)

Let me emphasize again that in the above statement dx is not just any increment of argument x, but an infinitesimal variable representing an increment converging to zero.
Similarly, df(x₀) is an infinitesimal variable representing an infinitesimal function increment during the process of an increment of an argument converging to zero.

From the definition of a differential
df(x₀)=f ^I(x₀)·dx
we see that differential is a function of two arguments: a fixed point x₀ within a domain of function f(x) and an infinitesimal increment of an argument dx.
Since x₀ is any fixed point, we can talk about a function differential at any value of argument x and use the notation df(x):
df(x)=f ^I(x)·dx

Here is an illustration of a concept of a differential.

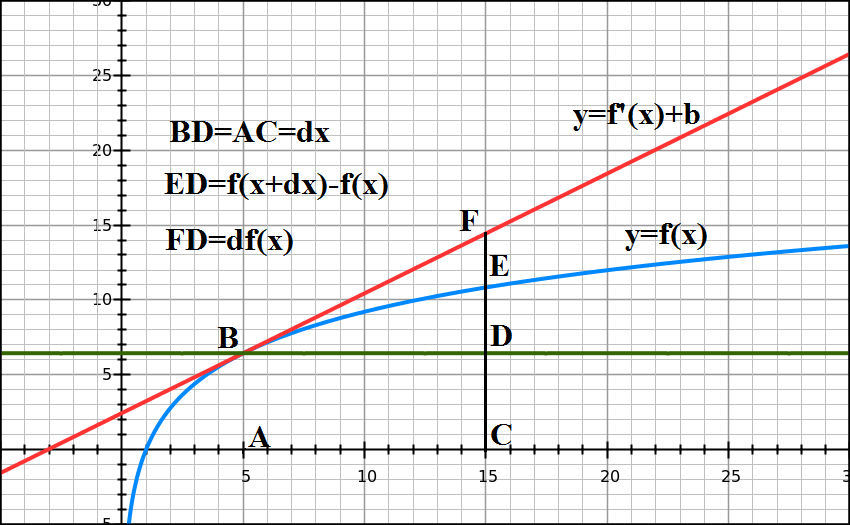
The blue line represents a function, red line - a tangential to it at point A.
Segment BD=AC represents an increment of the argument.
Segment DE is an increment of a function.
Segment DF is function's differential - an increment of a value along the tangential line proportional to the increment of the argument.
When point C moves closer to point A, decreasing the increment of the argument, both segments DE and DF decrease as well, while points E and Fare getting closer to each other, illustrating that increment of a function and its differential are infinitesimals if the increment of the argument is infinitesimal.
What's extremely important is that these two infinitesimals are of the same order as an increment of the argument, while difference between them, segment EF, is an infinitesimal of a higher order.

Recall the Taylor series for function f(x) with expansion center x₀:
f(x)=Σ_n≥0[f ⁽ⁿ⁾(x₀)·(x−x₀)ⁿ/(n!)]

Let's set
dx=x−x₀,
Δf(x₀)=f(x)−f(x₀)
and present this series as follows:
Δf(x₀) =
= f ^I(x₀)·dx+f ^II(x₀)·(dx)²/2+...
According to our definition of the differential, this can be expressed as
Δf(x₀) = df(x₀) + o(dx)
which illustrates the same concept: increment of a function is of the same order as its differential and they differ by an infinitesimal of a higher order than increment of the argument.

It's appropriate to note here that the concept of a differential of a function justifies the Leibniz's notation for a derivative:
f ^I(x) = df(x)/dx

Conclusion

Differential df(x₀) of a function f(x) at some fixed point x₀ of its argument is an infinitesimal variable proportional to infinitesimal increment of the argument dx with a coefficient of proportionality equaled to a derivative of this function at chosen point x₀:
df(x₀) = f ^I(x₀)·dx

Differential differs from increment in a sense that increment is a fixed difference between two values, while differential is an infinitesimal variable.
Thus, Δx is a fixed number that is equal to a difference between the incremented value of argument x=x₁ and its base value x=x₀:
Δx = x₁ − x₀
But differential is an infinitesimal variable {x₁ − x₀} in the process of x₁→x₀.
As soon as we switch from a fixed Δx to a process by considering Δx→0, increment of an argument Δx becomes its differential dx.

Similarly, Δf(x) is a fixed number that is equal to a difference between the value of a function at incremented value of the argument and the value of a function at the base value of the argument:
Δf(x) = f(x₁) − f(x₀)
As x₁→x₀, function increment Δf(x) is getting smaller and relative difference between its values and corresponding values of differential df(x₀) are getting smaller as well in a sense that
lim_Δx→0[Δf(x)]/df(x) = 1
because
lim_Δx→0[Δf(x)]/Δx = f ^I(x)
while
df(x)/dx = f ^I(x)
and dx means the same as Δx→0, that is a process of infinitely decreasing increment of an argument.