Unizor - Derivatives -Problems 4

Notes to a video lecture on http://www.unizor.com

Derivatives - Problems 4

Problem 4.1
For an implicitly defined function
x=x(t),
y=y(t)
find the second derivative
y''_xx(t) = d²y/dx².

Solution
First derivative dy/dx was discussed in the lecture on differentiation of implicitly defined function and is
y'_x(t) = dy(t)/dx(t) = [dy(t)/dt]/[dx(t)/dt]
The second derivative is a derivative of the first derivative:
y''_xx(t) = d/dx[y'_x(t)] =
= d/dx{[dy(t)/dt] / [dx(t)/dt]} =
= d/dx[y'_t(t)/x'_t(t)] =
= {d/dt[y'_t(t)/x'_t(t)]}/[dx(t)/dt]=
= {d/dt[y'_t(t)/x'_t(t)]} / x'_t(t) =
= [y''_tt(t)·x'_t(t)−y'_t(t)·x''_t(t)] / {[x'_t(t)]²·x'_t(t)} =
= [y''_tt(t)·x'_t(t)−y'_t(t)·x''_t(t)] / [x'_t(t)]³ =

Problem 4.2
Using the results of Problem 4.1, find the second derivative of parametrically defined function
x=arctan(t),
y=ln(1+t²)

Answer
y''_xx(t) = 2+2·t²

Problem 4.3
Using the results of Problem 4.1, find the second derivative of parametrically defined function
x=cos(2t),
y=sin²(t)

Answer
y''_xx(t) = 0
This prompts that y as a function of x must be a straight line.
Indeed, since
x=cos(2t)=1−2sin²(t),
it follows that
x+2y=1 and
y = (1−x)/2.
Graph of this function is below

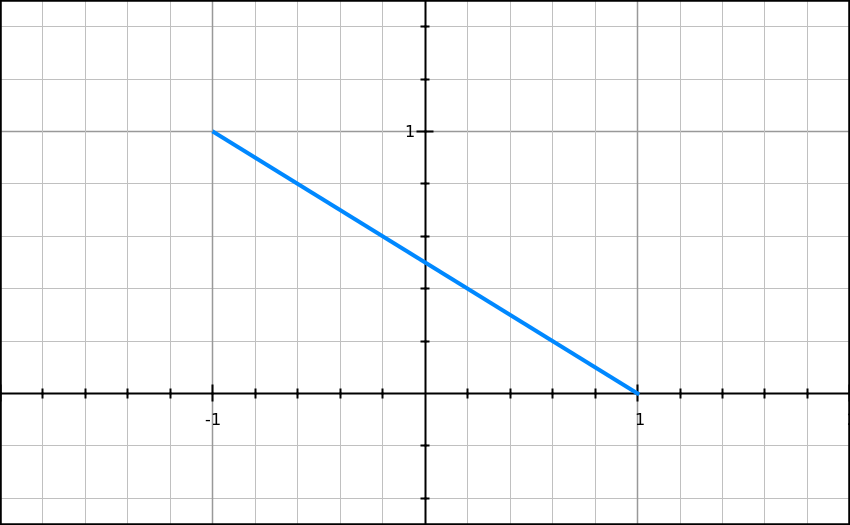
The parametric definition of this function puts restrictions on its domain
−1 ≤ x ≤ 1
and range
0 ≤ y ≤ 1.
But within these boundaries y(x) is a linear function.

Problem 4.4
Using the results of Problem 4.1, find the second derivative of parametrically defined function
x=cos(2t),
y=t²

Answer
y''_xx(t) = [sin(2t)−2t·cos(2t)] / [2sin³(2t)]