Unizor - Definite Integrals - Area under Curve

Notes to a video lecture on http://www.unizor.com

Definite Integrals -
Area under Curve

Consider the following problem.
Given a smooth function f(x) (we will always consider smooth functions in terms of continuity and sufficient differentiability), with non-negative values (that is, f(x) ≥ 0), defined on a closed segment [a, b] and represented by its graph on (X,Y) coordinate plane.

In the following we will use the word "area" in a sense of a two-dimensional part of a plane and as a quantitative measure of this part of plane. The context would clarify which one it is used in every case.

Our task is to find the "area under curve" - the measure of a part of coordinate plane bounded on the top by a graph of this function, on the bottom - the X-axis, on the left - by a line x = a and on the right - by a line x = b.
This area looks like this gray shaded part of a plane (for now, do not pay attention to what's written inside this area):


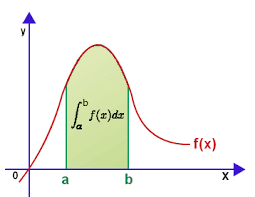
There is no ready to use formula for such an area. We do know how the area of a rectangle is defined, it is a product of its two dimensions - length multiplied by width, but not of such a complicated figure as the one we consider now.
We really have to define what the area of this figure is and then attempt to calculate it based on values of function f(x) on segment [a, b].
We did have a similar problem in Geometry with the area of a circle, and approached it as a sequence of approximations of a complex figure with simple ones. Let's do the same now.

We will use certain intuitive considerations to define the "area under curve" and will prove that this definition is mathematically valid.

The process of approximation starts with dividing segment [a, b] into N intervals by points a=x₀, x₁, x₂, x₃...x_N=b, and constructing rectangles, based on each interval [x_i−1, x_i], having the height equaled to a minimum value m_i of function f(x) on this interval, similar to the following picture (consider only light blue rectangles)


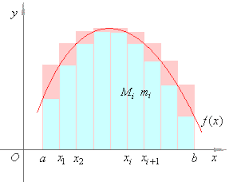
All the light blue rectangles are completely below the curve (since their heights are minimums of the function values on each interval) and, therefore, the sum of their areas does not exceed the intuitively understood "area under curve".

Alternatively, we can consider a set of rectangles built on the same intervals but of the height equaled to a maximum value M_i of function f(x) on each interval (consider now pink extension of light blue rectangles).
New taller rectangles are higher than the curve and, therefore, the sum of their areas is not less than the intuitively understood "area under curve".

Notice that the union of all blue rectangles resembles the figure we are trying to determine the area of. So, the sum of areas of all rectangles is close to the "area under curve", while always being less than "area under curve".
This sum of areas of rectangles can be expressed by a formula
s_N = Σ_i∈[1,N]m_i·(x_i−x_i−1) = Σ_i∈[1,N]m_i·Δx_i−1
where Δx_i−1 = x_i−x_i−1, which is the width of each interval.

Adding pink extension, we note that the sum of these taller rectangles also approximates the "area under curve", while being larger than it.
This sum of areas of rectangles can be expressed by a formula
S_N = Σ_i∈[1,N]M_i·(x_i−x_i−1) = Σ_i∈[1,N]M_i·Δx_i−1
where Δx_i−1 = x_i−x_i−1, which is the width of each interval.

Both approximations seem to be better if the number of intervals N we divide our segment [a, b] is large. And the larger is N - the better our approximation will be.

This can be confirmed by the following obvious statements.
If we divide any existing interval in two parts, build two rectangles instead of one and calculate the sum of areas of these rectangles, sum s_N, based on minimum values of function f(x), will increase and sum S_N, based on maximum values of function f(x), will decrease.

Let's continue adding points of partitioning to infinity such that the largest interval's width converges to zero.
During this process sum s_N will monotonically increase or stay the same, but not decrease, while being bounded from above by any S_N; and sum S_Nwill monotonically decrease or stay the same, but not increase, while being bounded from below by any s_N.
These properties of sequences s_N and S_N are sufficient to state that both have limits:
lim s_N = s_∞
lim S_N = S_∞
where s_∞ ≤ S_∞, and the limit is understood in terms of making partitioning of segment [a, b] finer and finer with the largest interval shrinking in width to zero.

So, our next step in the process of approximation of the "area under curve" is to divide each of N intervals in two parts, getting twice as many intervals and build twice as many narrower rectangles.
Blue rectangles lying below the curve will be inscribed "tighter" to the area under the graph of function f(x), so the approximation of the "area under curve" with s_N will be better.
Blue rectangles with pink extensions lying above the curve will encompass "tighter" the area under the graph of function f(x), so the approximation of the "area under curve" with S_N will also be better.

As the number of intervals grows and the width of the largest interval becomes an infinitesimal variable, the difference between s_N and S_Nbecomes smaller and smaller.
If we can prove that this difference converges to zero, as long as the width of the largest interval converges to zero, it would be a sufficient foundation to call the limits s_∞or S_∞ (they are the same) the area under curve.

Proof

Recall that we are proving this theorem for sufficiently smooth functions. They and their derivatives are assumed to be continuous. In general, the theorem can be proven under weaker conditions (differentiability is not a necessary condition), but for the purposes of this course we are choosing the easier proof that is valid for smooth functions.

Consider the i-th interval [x_i−1, x_i].
Assume that function f(x) reaches its maximum M_i on this interval at point ξ_i∈[x_i−1, x_i] and it reaches its minimum m_ion this interval at point η_i∈[x_i−1, x_i].

According to Lagrange Mean Value Theorem, there is a point ζ_i∈[ξ_i, η_i]. such that
f ^I(ζ_i)·(ξ_i−η_i) = M_i−m_i
from which we can derive the upper boundary for |M_i−m_i|:
|M_i−m_i| ≤ max_[a,b]{|f ^I(x)|} · max_i{|x_i−x_i−1|}

Here max_[a,b]{|f ^I(x)|} represents the maximum of the absolute value of the first derivative of f(x) on segment [a,b], which is some constant since f(x) is a smooth function, let's call it K.
The second multiplier max_i{|x_i−x_i−1|} represents the maximum width of intervals in our partitioning of the original segment into N parts, let's call it W_N.

So, we conclude that
|M_i−m_i| ≤ K·W_N
where W_N (the widest interval) is assumed to be an infinitesimal variable as N→∞.

Now we can evaluate the difference S_N−s_N:
S_N−s_N = Σ_i∈[1,N](M_i−m_i)·(x_i−x_i−1) ≤ K·W_N·Σ_i∈[1,N](x_i−x_i−1) = K·W_N·(b−a)

The last expression contains an infinitesimal variable W_N multiplied by two constants.
Therefore, we have proven that the difference between upper S_N and lower s_N boundaries of "area under curve" is infinitesimal variable if the widest interval of partitioning of our segment [a,b] shrinks in width to zero.

From this follows that if, instead of choosing minimum value m_i or maximum value M_i on each interval [x_i−1,x_i] as the height of a corresponding rectangle, we choose any value of a function f(x) on this interval, the limit will be the same since the corresponding sum of areas of these rectangles will always be between s_N and S_N.

We can conclude now that if we define the area under curve as a limit of sum of areas of rectangles based on intervals we divide the original segment into with the heights equal to values of our function in any point inside the corresponding intervals (left margin x_i−1, right margin x_i, maximum point ξ_i, minimum point η_i or any other), the limit will be the same as long as the widest interval's width converges to zero.

That proves the mathematical correctness of this definition. The area under curve, as defined, exists (since the limit of the sums of rectangles exist) and unique (since the limit does not depend on how we proceed partitioning the original segment and how we choose the points where the function value for the height of rectangle is chosen).

End of proof.