Notes to a video lecture on http://www.unizor.com
Gravity Integration 3 -
Thin Spherical Shell
1. Determine the potential of the gravitational field of a uniform infinitesimally thin spherical shell at any point outside it.
Let's establish a system of coordinates with a spherical shell's center at the origin of coordinates and X-axis going through a point of interest P, where we have to determine the gravitational potential.
Assume that the sphere's radius is R and the mass is M. Then its surface is 4πR² and the mass density per unit of surface area is ρ=M/(4πR²).
Assume further that X-coordinate of a point P, where we want to calculate the gravitational potential, is H, which is greater than the radius of a spherical shell R.
If, instead of a spherical shell, we had a point mass M concentrated in its center at point O(0,0,0), its gravitational potential at a point P would be
V0 = −G·M/H
(remember that the gravitational potential is negative, as it equals to amount of work needed to bring a unit of mass from infinity to point P, and the field performs this work for us, so we perform negative work).
As we know, gravitational potential is additive, that is the potential of a combined gravitational field produced by two or more sources of gravitation at some point equals to sum of their individual gravitational potentials at this point.
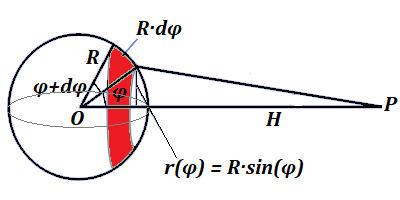
To calculate a gravitational potential of an infinitesimally thin spherical shell at point P on the X-axis, let's divide a spherical shell into infinite number of infinitesimally thin rings that are parallel to the YZ-plane and, therefore, perpendicular to X-axis, that goes through a center of each ring.
The angle φ from X-axis (that is, from OP) to a radius from an origin of coordinates to any point on a ring will be our variable of integration.
Then the radius of a ring will be
r(φ) = R·sin(φ)
The distance from the origin of coordinates to a center of a ring is R·cos(φ).
The area of a ring between angles φ and φ+dφ will be equal to the product of infinitesimal width of a ring R·dφ and its circumference 2πR·sin(φ)
Therefore, the mass of a ring will be
dm(φ) = ρ·2πR²·sin(φ)·dφ =
= M·2πsin(φ)·dφ/(4π) =
= M·sin(φ)·dφ/2
Knowing the mass of a ring dm(φ), its radius r(φ) and the distance from the ring's center to point of interest P, that is equal to H−R·cos(φ), we can use the formula of the ring's potential from a previous lecture
V = −G·M /√R²+H²
substituting
dV(φ) instead of V
dm(φ) instead of M
H−R·cos(φ) instead of H
r(φ) instead of R
Therefore,
dV(φ) = −G·dm(φ) /√r²(φ)+[H−R·cos(φ)]² =
= −G·M·sin(φ)·dφ /2√R²+H²−2R·H·cos(φ)
Now all we need is to integrate this by φ in limits from 0 to π.
Substitute
y = √R²+H²−2R·H·cos(φ)
Incidentally, the geometric meaning of this value is the distance from point of interest P to any point on a ring for a particular angle φ.
Then
dy = R·H·sin(φ)·dφ /√R²+H²−2R·H·cos(φ)
The limits of integration for φ from 0 to π in terms of y are from |H−R| (which, for our case of point P being outside the sphere, equals to H−R) to H+R.
In terms of y
dV(y) = −G·M·dy /(2R·H)
which we have to integrate by y from H−R to H+R.
Simple integration of this function by y on a segment [H−R;H+R] produces −G·M·y/(2R·H) in limits from H−R to H+R:
V = −G·M·(H+R)/(2R·H) +
+ G·M·(H−R)/(2R·H) =
= −G·M/H
Remarkably, it's exactly the same gravitational potential, as if the whole mass was concentrated in a center of a spherical shell, as noted above as V0.
It's a justification for considering gravitational potential of space objects in many cases to be approximately equivalent to a potential of point-masses of the same mass concentrated in one point, the center of mass of an object.
2. Determine the potential of the gravitational field of a uniform infinitesimally thin spherical shell at any point inside it.
Using the same notation as in the previous case, this problem requires the distance from a point of interest P to a center of a spherical shell O to be less than the radius R of a spherical shell.
Doing exactly the same manipulation and substitution
y = √R²+H²−2R·H·cos(φ)
we see that the only difference from the previous case is in the limits of integration in terms of y.
The limits of integration for φ from 0 to π in terms of y are from |H−R| (which, in this case of point P being inside the sphere, equals to R−H) to H+R.
Integration by y on a segment [R−H;H+R] produces −G·M·y/(2R·H) in limits from R−H to H+R:
V = −G·M·(H+R)/(2R·H) + G·M·(R−H)/(2R·H) =
= −G·M/R
Remarkably, it's constant and is independent of the position of point P inside a spherical shell.
We have mentioned in the earlier lecture on gravitational field that in one dimensional case the gravitational force is a derivative of gravitational potential by distance from the source of gravity times mass of a probe object:
F(r)=G·M·m /r²=m·dV(r)/dr
The fact that the gravitational potential is constant and, therefore, its derivative is zero, signifies that there is no force of gravity inside a spherical shell. The forces of gravity from all directions nullify each other.
An intuitive explanation of this is in the fact that, if you consider any conical surface with a vertex at point P inside a sphere, cutting pieces of spherical shell's surface in both directions, the areas of the pieces will be proportional to a square of a distance from point P, while the gravitational forces produced by these pieces of surface are inversely proportional to a square of a distance from point P, thus both forces from opposite ends of a cone are equal in magnitude and opposite in direction, thus nullify each other.


No comments:
Post a Comment