Electricity in Transit
Let's discuss how electricity is delivered from the power plants to consumers.
The only way to deliver the electricity from the place it's generated to a place it's used is via electric wires.
Since the distance between the power plant and a consumer can be substantial, may be even hundreds of kilometers, the problem of losses of electric energy in transit because of wire resistance is extremely important.
Examine a simple electric circuit consisting of a source of electricity (generator) and a consumer (like an electric motor).
In theory, we have four places where electric energy is spent:
(a) inside a generator due to internal resistance,
(b) inside a wire from a generator to a motor due to wire resistance,
(c) inside a motor due to useful work the electricity does and internal resistance,
(d) inside a wire from a motor back to a generator due to wire resistance.

Obviously, only in a motor the energy is spent with some useful purpose, in other places the energy is spent just because it's unavoidable, that is wasted.
Amount of energy wasted to heat per unit of time due to wire resistance Wwire depends on the current running through wire Iwire and the wire resistance Rwire according to a formula
Wwire = I2wire·Rwire
For practical example, let's calculate the amount of energy wasted in some long piece of copper wire.
The resistance of a wire depends on resistivity of material it's made of ρ, is proportional to the length of a wire L and is inversely proportional to its cross-section area A
Rwire = ρ·L/A
For copper the resistivity is approximately
ρ≅1.70·10−8 Ω·m.
Assume, the combined wire length to and from a consumer of electricity is
L = 1 km = 1000 m
and its diameter is
D = 2 mm = 2·10−3 m,
which gives the area of its cross-section
A = π·D²/4 ≅ 3.14·10−6 m²
Then the resistance of this peace of wire is
Rwire ≅ 5.4 Ω
For example, we are supposed to run an electric motor working at voltage
Umot=220 volt
and delivering power of
Wmot=2.2 kilowatt.
Then the current it requires is
Imot = Wmot/Umot = 10 A
The current Imot=10 A must go through the wire
Iwire = Imot = 10 A
Then the amount of energy wasted to heat in the copper wire of resistance Rwire=5.4 Ω per unit of time (a second) is
Wwire = I²wire·Rwire = 540 W
For a price of about $0.1 per kilowatt this amounts to about $0.054 per second. For 24 hours uninterrupted work the financial waste amounts to $4,665, and that is every day of operation of one motor, which is absolutely unacceptable.
Reducing the resistance of a wire by making it thicker or using multiple parallel wires has its practical limitations because of cost of wires. Therefore, our solution to reduce the energy wasted to heat due to wire resistance, while staying within reasonable limits with the cost of a wire, must be related to reducing the current Iwire running through a wire without reduction of power that is supposed to be delivered to consumers of electricity.
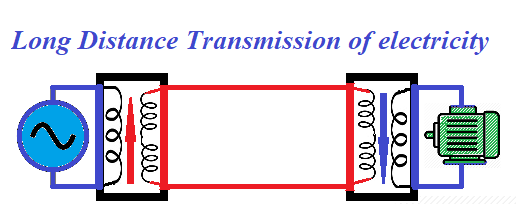
This can be accomplished by using transformers.
Immediately after generation, the alternating current is directed to a transformer that increases the voltage and proportionally decreases the amperage.
At the output of this transformer the voltage reaches thousands of volts - from low voltage of 1000V to ultra high voltage above 800,000V, depending on the length of wires from generators to consumers.
This high voltage electricity is delivered to consumers, where another transformers reduce the voltage to standard needed to run all their different devices.
Consumers of electricity get the voltage required to run their equipment, but the current running in the long wires between generators and consumers is low, thus reducing waste of electric energy.
Consider an example above with a motor that needs Wmot=2.2 kilowatt of electricity at voltage Umot=220 volt and, therefore, requires Imot=10 A electric current.
If, instead of transmitting electricity with these parameters, we increase the voltage by a transformer before sending it to long wires to, say, 2200V, thus proportionally reducing the amperage by the same factor, our amperage will be
A = W/U = 2200/2200 = 1A
Reducing the amperage from 10A to 1A reduces the energy waste by a factor of 100 because the heat formula depends on a square of amperage.
The distribution of electricity, therefore, should include transformers that increase the voltage before sending electricity along long wires and decrease it wherever it's needed for usage by consumers.
With this modification the picture that corresponds to practical aspects of distribution of electricity looks like this
To increase the electrical systems' reliability, improve the energy balancing and make sure of uninterrupted power supply, the sources of electrical energy (electric power plants and other installations producing electric energy) are combined into a network called the grid.
The principles of this networking are a subject of the next lecture.


No comments:
Post a Comment