Reflection Waves
Let's consider the same simple device as in the previous lecture - a cylinder of relatively small diameter with air and a piston in it, except this time we will examine what happens at the opposite to a piston end of a cylinder.

Let's give a single short and quick push to a piston down. As a result, a single parallel to a piston wave of a higher pressure air will start its way down a cylinder with certain speed v that depends on properties of air, its temperature, initial pressure etc.
When this wave reaches the bottom of a cylinder, a thin layer of higher pressure air will develop there. Since the bottom of a cylinder prevents a wave to go farther, the higher pressure air will release its pressure back to a layer above it. This constitutes a reflection of the wave.
After such a reflection the wave will go to the opposite direction (upward on the picture) until it reaches the top, where piston is positioned. At this moment, since piston is not moving, it will play the same role as a bottom of a cylinder before, it will reflect the wave.
Ideally, this reciprocal movement of a wave can continue, it will be reflected from both ends of a cylinder indefinitely.
Practically, the energy of the initial push of a piston will gradually dissipate into more intense movement of the air molecules, which means that the temperature of the air will increase slightly.
Consider now a harmonic oscillation of a piston. It produces pressure waves in the air propagated downward. But now we know that they reflect from the bottom of a cylinder and propagate upwards.
This results in a very complex superposition of two sets of waves, one going downwards and another upwards.
There is, generally speaking, a shift in phase between these two sets of waves that depends on the speed of wave propagation and the length of a cylinder.
The resulting picture of air pressure will look quite chaotic and far from harmonic oscillations of a piston. Yet, it's just a simple superposition of waves moving in two opposite directions.
Imagine a complexity of a sound distribution in an opera house with air pressure waves, originated by a person singing on a stage, reflected from all hard surfaces and mixing in time and space with other waves. Unless special design measures are taken, the quality of a sound will be very low.
Even in such a simple case as recording these lectures we had to use special directional microphone that suppresses sounds from all directions except the main one directed onto a primary source of sound. In addition, to weaken the reflection, we open closets on the opposite wall to weaken the strength of reflected sound waves.
Let's analyze the reflection of a simple flat wave from a surface that is not perpendicular to the wave front, keeping in mind the Law of Reflection, that is, the angle of incidence equals to the angle of reflection.
Assume that our flat wave consists of only two molecules of air a and b that hit a surface AB at 45° angle.
A thin line between these molecules represents a wave's front, which is perpendicular to their trajectories.
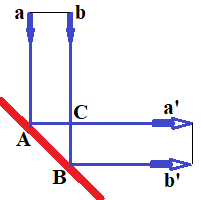
From a picture above and some elementary geometry it's obvious that reflected wave will be exactly as original, except its direction will be perpendicular to the original's one.
Indeed, a and b move on parallel trajectories with the same speed, covering the same distance in equal times. So, molecule a will come to point C at the same time as molecule b reaches point B. After that a and b continue their parallel movement and the new wave's front is still perpendicular to molecules' trajectories.
Even if the angle of a reflecting surface is not 45° to a direction of the original wave, the reflected wave will still be a flat wave with only direction changed.
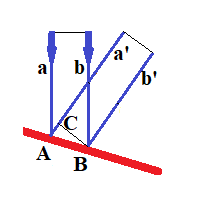
It's easy to prove that molecule a will reach point C at the same time as molecule b comes to point B. After that both molecules continue their straight movement with a wave front perpendicular to their parallel trajectories.
We should not think about waves and their reflections as a flow of the same molecules toward a reflective surface, reflecting from it and continuing the movement. Different crests of waves have different molecules. But the movement of one molecule is transferred to its neighbor in the direction of a wave propagation as if they are connected with tiny springs.
Another good comparison of this process is the balls on a billiard table. When a ball hits another ball straight on, it stops and the other ball continues the movement in the same direction. If the hit is not exactly straight on, the impulse of a hitting ball will be distributed among two balls, but their sum will be equal to the original impulse.
So, the energy and impulse are transferred in some direction without carriers of this energy and impulse actually moving all the way to the end of a road, but rather by transferring this energy and impulse to other carriers, like in the relay race.
Let's return back to a case when a flat solid surface is perpendicular to a direction of propagation of the flat waves, like a bottom of a cylinder described above.
As mentioned above, reflected from this obstacle waves will be reflected in the opposite direction, thus interfering with original waves.
Both oscillations, downwards and upwards, have exactly the same period T and wavelength λ. Their speeds v are equal by absolute value, but oppositely directed.
Depending on difference in phase, superposition of these two waves can produce different interesting effects.
An oscillation of air in a cylinder, produced by an oscillation of a piston, is just a periodic higher and lower concentration of molecules of air (that is, higher or lower pressure) with the waves of high concentration moving from a piston down a cylinder with some speed.
Add to this picture reflected waves formed at the opposite end of a cylinder - waves of higher and lower concentration of molecules of air (that is, higher or lower pressure) moving up the cylinder.
Both processes mix together in a superposition. When a wave crest from a piston reaches some layer of air, it pushes this layer down.
When the opposite reflected wave crest reaches the same layer, it pushes this layer up.
With proper difference in phase, that depends on the length of cylinder relatively to a wavelength λ, there might be a situation when the same layer of air in a cylinder is simultaneously pushed down by a wave crest from a piston and up by a reflected wave crest. As a result, this layer will be squeezed from both ends, the pressure in this layer will become higher.
For similar reasons the layer on a distance λ/2 (half a wavelength) from the one that is squeezed from both sides will be thinner, and the pressure inside this layer will be lower.
In T/2 (half a period) time the area that used to be with higher concentration of molecules will become thinner, as its molecules will move in opposite directions, thus making areas on a distance of half a wavelength around become more concentrated, that is with higher pressure.
This is a case of waves formed by two opposite sources of oscillation - by a piston and by a reflection from the bottom of a cylinder.
The distance between a piston and a bottom of a cylinder will be divided in layers of half a wavelength thick. Each layer will be squeezed and stretched every half a period time, becoming more concentrated and less concentrated than its neighbors.
Each layer would look like an accordion gaining some air inside and squeezing it out every half a period time.
So, entire air in a cylinder can be viewed as a series of sidewise connected accordions. When every other one is synchronously squeezed, both its neighbors are stretched and, when every other one is synchronously stretched, its both neighbors squeezed.
The crests of these waves of higher and lower pressure will not travel, as in a case without reflection, but will stand on the same place. This phenomenon is known as standing waves.


No comments:
Post a Comment