Real Numbers - Approximation
From Exact to Approximation
As we know, we can use decimal notation to represent real numbers.
Integer numbers are represented in a decimal form without decimal point.
Rational non-integer numbers use finite or infinite periodical sequence of decimal digits after the decimal point to represent their fractional part.
Irrational numbers in decimal form have infinite sequence of non-periodical decimal digits after the decimal point.
In this lecture we will talk about how to use approximation of those real numbers, whose exact decimal representation is impossible (because they have an infinite sequence of decimal digits after the decimal point) or inconvenient (for lengthy sequences of digits) to show.
As a simple example, consider a task of measuring 1/7th of
The metric ruler has centimeters and millimeters on it. It means, it's impossible to measure exactly 1/7th of 1 meter because
1/7 = 0.(142857) - an infinite periodical fraction.
The best we can do is to measure 14 cm and either 2 mm or 3 mm because
0.142 < 1/7 < 0.143.
It's better to choose
14 cm and 3 mm
because the exact value
The need for approximation in the above example is dictated by our practical ability and limitations to deal with exact number. These limitations determined the level of precision required from approximation -
Consider another example - a population of the United States of America.
Obviously, we cannot know the exact number of people living in the country because people get born, die, move to another country or come from another country all the time.
So, for practical reasons we approximate this number to, say, millions. If we say that the population of the USA is, approximately, 330 millions, it's sufficient to address most issues related to the population, like how much water is consumed by all people in a country or average density of the population.
Again, practical considerations dictate certain level of approximation, its precision -
Now we approach the approximation more formally.
The purpose of the approximation is to represent the real number in question by another number, according to certain rules:
1. Out of all real numbers we choose a countable subset of numbers equally spaced from each other, we will call them base numbers.
For example, we can have a set of all integer numbers or a set of numbers, starting at zero, with a distance of 1000 from each other, or a set of numbers, starting at zero, with a distance of 0.001 from each other.
In the example above, when we measured the length with a precision of
In the example above, when we counted people in millions, our base numbers are 0, 1000000, 2000000, 3000000 etc.
This set of base numbers determines the possible approximate values for numbers we would like to represent.
2. For any real number we would like to represent approximately we use the closest to it number from a set of base numbers chosen above.
3. A special case, when the exact number is equidistant from both base numbers, the one less and the one greater than it, needs special consideration that we discuss below.
Example 1
We need to find a length of a side of a square whose area is
From geometry we know that this side should be equal to a square root of 2 meters, but it's an irrational number, so we cannot represent it exactly in decimal notation needed for practical purposes.
We choose the precision sufficient for our practical purposes and practically achievable using the tools at hand (say, a measuring tape with meters and centimeters), to be 1 centimeter, that is 0.01 of a meter.
This determines the base numbers for our approximation 0, 0.01, 0.02, 0.03 etc.
Then we approximate square root of 2 beyond the second digit after the decimal point to determine which base number it's closest to:
√2 ≅ 1.414
which is closer to a base number 1.41 than to 1.42.
So, with a precision of 0.01 (that is, in centimeters) the size of a side of a square with area of 2 square meters equals to
1.41 m
Example 2
The distance between two cities is represented in kilometers. The exact distance is usually measured between the main post offices in these cities, and it's never equals to an exact integer number of kilometers.
For example, the distance from Hanoi to Shanghai is listed as 1925 km.
Obviously, it's an approximation to an integer number of kilometers.
The actual exact distance from the entrance door to Hanoi's main post office to the entrance door to Shanghai's main post office along the shortest route might be something like 1924.532 km (that is, 1924 km and 532 m), but we replaced the exact distance with its approximation as a more practical value.
Special case
It's logical and reasonable to approximate any exact number with a base number that is closest to it.
Consider now a case when an exact number is equidistant from two base numbers, one below and another above it.
For example, we would like to approximate to a precision of 1000 (so, base numbers are 0, 1000, 2000, 3000 etc.) and a number we want to approximate is 56500, which is equidistant from base numbers 56000 and 57000.
Or we would like to approximate to a precision of 0.01 (so, base numbers are 0, 0.01, 0.02, 0.03 etc.) and a number we want to approximate is 8.565, which is equidistant from base numbers 8.56 and 8.57.
This is a dilemma that must be resolved by some rule imposed on the process of approximation.
Unfortunately, there are more than one rule, and these rules might contradict each other. Fortunately, one rule does play a dominant role and used in most cases. This is the one we would like to specify as the one to follow, unless a specific other rule is mentioned.
In case an exact number is equidistant from two base numbers, one below and one above it, choose the one that has higher absolute value.
Examples:
Precision is 0.001,
exact value is 25.6575,
approximate value is 25.658.
Precision is 0.001,
exact value is −2.7595,
approximate value is −2.760.
Precision is 10,
exact value is 25,
approximate value is 30.
Precision is 10,
exact value is −95,
approximate value is −100.
From Approximation to Exact
Let's reverse the logic and try to evaluate the exact number, if it's approximation is given.
Again, a lot depends on the precision of approximation. The more precise approximation was applied to exact number - the closer the approximation is to it and, therefore, more precise evaluation of the exact number can be performed, if an approximate number is known.
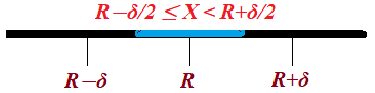
Let's assume, we have an exact number X and its approximate value with precision δ is R. It means that among base values R−δ, R and R+δ the number X is closer to R than to R−δ or R+δ.
If so, the following inequality must hold
R−δ/2 ≤ X < R+δ/2
as illustrated below with the blue area representing the possible values of X, if R is its approximation with precision δ.
So, if approximate value of the number of people living in New York in 2019 was 8.419 million (implying the precision δ=0.001 of a million, that is δ=1000), the exact number was greater or equal to 8.4185 million (that is, 8,418,500), but less than 8.4195 million (that is, 8,419,500).
If approximate value for number π is 3.14 (implying the precision δ=0.01), that exact ratio of a circumference of any circle to its diameter is greater or equal to 3.135, but less than 3.145.
As you see, the range of values for an unknown exact number X around its known approximation R is equal to a precision δ of approximation:
(R+δ/2) − (R−δ/2) = δ
Approximation Error
What happens, when we make some arithmetic operation with approximate values?
Unfortunately, the error of approximation is accumulated and growing.
Let unknown exact number X be approximated by a known number R with precision δ. Let unknown exact number Y - by a known number S with the same precision δ.
Let's determine the range of values for X+Y.
According to the laws of approximation,
R−δ/2 ≤ X < R+δ/2
S−δ/2 ≤ Y < S+δ/2
Then, adding these inequalities, we obtain
R+S−δ ≤ X+Y < R+S+δ
The range of values for X+Y is
(R+S+δ) − (R+S−δ) = 2δ
As you see, the precision of evaluating the sum of two exact values, using the sum of their approximations, is now 2δ. So, the quality of approximation is worsening, when we do arithmetic operations with approximate values to evaluate the result of these operations with unknown exact values.
Obviously, similar worsening of the quality of approximation is observed with any other operation (like subtraction, multiplication, division etc.), when we use approximate values in order to evaluate the result of this operation on unknown exact values.
For example, we need to evaluate the rise of the sea level in 10 years from now.
According to EPA, if sea level in 1880 is taken as level zero, by 1994 this level was
From 1994 to 2019 the sea level was rising by an average factor of
Let's disregard extreme values and limit ourselves to 68% probability of the exact value of the average factor of the rise of a sea level to be within [μ−σ;μ+σ] range, that is from 1.004 to 1.028.
Then in 10 years from 2019 the minimum sea level will be
Wmin = 240.775·1.00410 ≅ 251 (millimeters above 1880 level)
while its maximum will be
Wmin = 240.775·1.02810 ≅ 317 (millimeters above 1880 level)
Which numbers to believe?
What is the estimate of the sea level in 100 years?
Wmin = 240.775·1.004100 ≅
≅ 359 mm = 0.359 meters above 1880 level
Wmin = 240.775·1.028100 ≅
≅ 3810 mm = 3.81 meters above 1880 level
As you see, the difference is dramatic! This proves how skeptical we have to be when hearing different predictions about future.


1 comment:
This is an amazing blog and I found it very informative. You have done a great job
and keep writing such wonderful articles. To get more information about how many ounces are in one fourth of a cup then
Please click here:
https://howtodiscuss.com/t/how-many-ounces-in-a-quarter-cup/14700
Post a Comment