Point Light Hologram
This lecture is about an idea that is fundamental to understand the holography.
We will explain how a position of a point light (a point in space that emits radial rays of light) can be recorded and, later on, presented, when it's no longer there.
What is discussed in this lecture is a kind of a "thought experiment", but, properly modified, it can be actually implemented, which the progress of holography has achieved.
Assume, we have a point source of monochromatic light of wave length λ.
Our first task is somehow record its position in space relatively to some recording media (a screen).
The second task, when the source of light is no longer there, is to recreate an image of this point light, like a bright point in space, positioned relatively to a screen in the same spot as the original source of light.
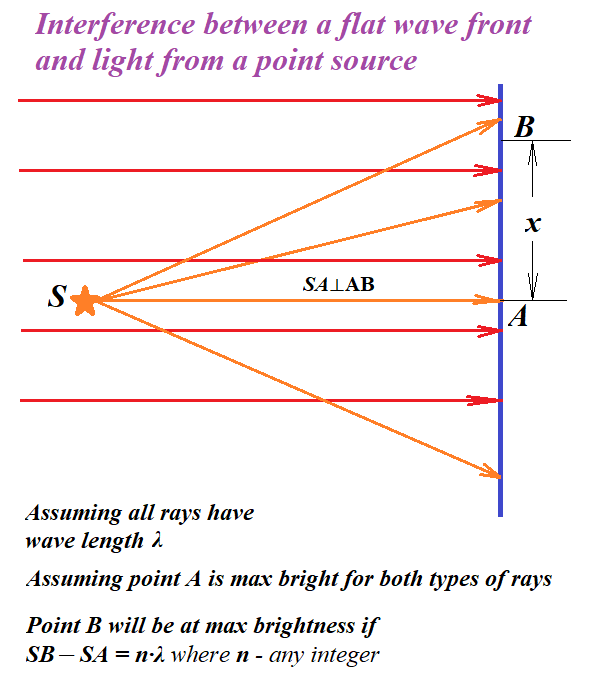
The picture below proposes a solution to the first task.
The point source of monochromatic light (orange star S) sheds light (radial orange rays SA, SB and others) onto some flat screen AB, which will be our recording medium.
Assume, SA⊥AB.
The distance between a point light S and a screen AB is SA=d.
We assume that all the rays issued by a source S have the same wave length λ and are issued in phase, that is, coming from the source S, they are coherent.
At the same time a set of parallel monochromatic light rays of the same wave length λ (red rays on the picture), also in phase, are directed perpendicularly to screen AB.
NOTE: the radial light rays are orange and parallel are red only to differentiate them on a picture below, their real color depends on the wave length that is the same for all of them.
(click right mouse and open this picture in another tab to see it in full format)
What we will observe on screen AB is the interference picture between two sets of light rays - radial and parallel.
Let's analyze what kind of interference picture we will see on the screen AB.
To simplify this analysis without jeopardizing the logic, assume that both radial and parallel rays that come to point A are in phase and, therefore, constructively interfere with each other, making point A a bright spot on the screen.
Consider any point B on a screen on a distance x from A. Point B will be bright if the radial ray SB and the corresponding parallel ray coming to point B are in phase.
Since all parallel rays are in phase among themselves, and a parallel ray coming to point A is in phase with corresponding radial ray SA, we will have a bright spot at point B if rays SB and SA are in phase, that is
SB − SA = n·λ
where
n is any non-negative integer number and
λ is the wave length (the same for radial and parallel rays).
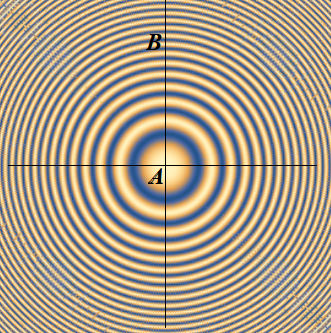
Incidentally, for any fixed n all bright points B on a flat screen such that SB−SA=n·λ form a circle centered at point A. So, for different n we will see different concentric bright circles, all centered at point A. They are called Newton's rings.
Below is a sample of a real interference picture that can be observed on a screen in a setting similar to the one described above.
From the properties of the right triangle ΔSAB, considering SA=d and AB=x, follows
SB² = d² + x²
Therefore,
SB − SA = n·λ = √d² + x² − d
From this follows:
(n·λ + d)² = d² + x²
x² = (n·λ+d)² − d²
The above is a condition for point B on the distance x from the midpoint of a screen A to be a bright spot.
Assigning an integer variable n different values allows to find distances xn of bright spots (more precisely, radii of bright concentric circles) on a screen by resolving the above equation for x.
This results in the following expression for xn as a function of distance d between a point light S and a screen and non-negative integer number n:
xn = √(n·λ+d)² − d²
For n=0 the distance of the bright spot from the midpoint A will be
x0 = 0, that is, it will coincide with midpoint A.
For n=1 the bright spot will have a distance from the midpoint A
x1 = √(λ+d)² − d²
For n=2 the bright spot will have a distance from the midpoint A
x2 = √(2λ+d)² − d²
etc.
An interesting math exercise would be to find how close to each other will be bright circles on a screen.
In other words, how xn+1−xn behaves as index n increasing.
It can be shown that this distance is monotonically diminishes from its maximum value
x1 = √(λ+d)²−d² = √λ²+2λd
(that is greater than λ) to the wave length λ, as index n increases.
That is,
limn→∞(xn+1−xn) = λ
As an example, let's calculate the radii x1, x2 and x3 of the first three bright circles around midpoint A for the monochromatic green light of
Let's use micrometers, also known as microns (μm) as units of distance, with 1000nm=1μm and 1,000,000μm=1m.
x1 ≅ 31.6 μm
x2 ≅ 44.7 μm
x3 ≅ 54.8 μm
Therefore, the distance between x0=0 and x1 is 31.6 microns, from x1 to x2 it's 13.1 microns, from x2 to x3 it's 10.1 microns.
To see the diminishing distance between concentric bright circles, let's calculate x97, x98 and x99.
x97 ≅ 315.2 μm
x98 ≅ 316.9 μm
x99 ≅ 318.5 μm
The distance between x97 and x98 is 1.7 microns, from x98 to x99 it's 1.6 microns.
As you see, the bright circles are getting closer to each other as we observe them at a longer distance from the midpoint A.
As n→∞, this distance will get closer and closer to 0.5 microns - the wave length of the monochromatic green light we used in this experiment.
So, we have a pretty good idea of the interference picture developed on a screen.
This interference picture is very specific to a position of our point light S. So, if we will be able to record this interference picture on a screen, there is a possibility to recreate the position of point light S.
Assume, our screen is made of transparent glass. Now, knowing locations of all bright circles on a screen, let's paint in black all the dark areas on a screen (they are circular too), the bright circles remain transparent.
Now our screen represents the recording of the interference picture, which is very specific for a location of the point light S.
Our first task to record the position of a point light is completed. We can take away now both sources of monochromatic light (radial and parallel rays on a picture above).
The second task is to recreate the point light at a location where it was relative to a screen using the information recorded on a screen (concentric black and transparent areas).
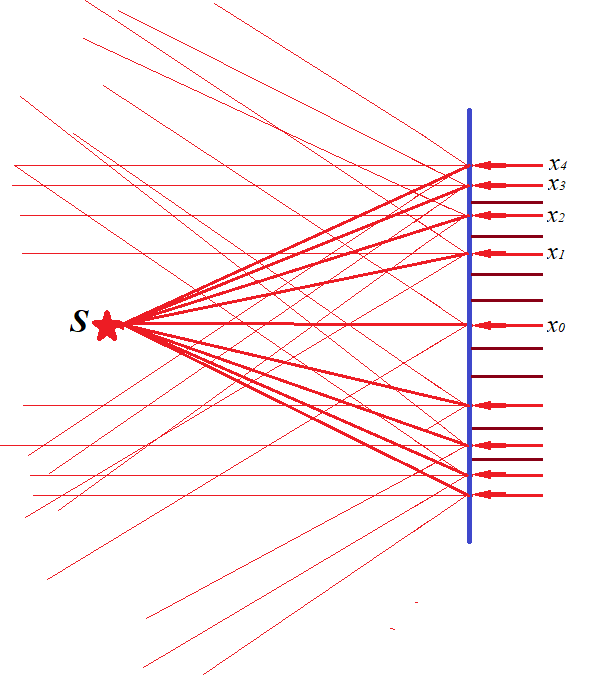
Let's take the source of parallel monochromatic rays used before and transfer it behind the screen, so it shines parallel rays of light perpendicularly to a surface of a screen from behind, as presented on a picture below.
(click right mouse and open this picture in another tab to see it in full format)
Obviously, only the rays that hit the transparent circles at radii x0, x1, x2, x3 etc. from a screen's midpoint, where the bright spots used to be, will go through a screen. These rays are presented as red and have arrows at the end.
The others (brown without arrows) will be stopped by a screen.
According to Huygens principle, each ray of light that goes through transparent areas of a screen is a source of secondary waves emitted radially at an exit from a screen, as presented on a picture above.
All these secondary light rays will interfere with each other. But, if we consider only the rays going from each transparent area of a screen to a point S, where the point light used to be, they all will be in phase and, therefore, constructively interfere with each other.
Indeed, the difference in distance from the midpoint A to point S and from a circle of radius x1 to point S is exactly the wave length λ.
The difference in length from the midpoint A to point S and from a circle of radius x2 to point S is two wave lengths 2λ.
Therefore, the point S will be bright, since rays from each transparent circle will come to it in phase and intensify each other at this point.
What's important is that all rays that go through a screen will constructively or destructively interfere with each other in all other points of space as well, but point S will definitely stand out as the brightest spot because significantly more light rays (actually, as many as the number of transparent circle) will come to it in phase.
If we understand the main principle of recreating a point source of monochromatic light, let's try to make this principle more practical.
Of course, we cannot paint black circles on a screen with a precision required for this experiment to actually implement the process.
What we can do, however, is to cover a screen with photosensitive layer containing silver compound that, being exposed to light at the bright spots on an interference image, makes only these spots reflective.
To create an image of a point light at location S, instead of directing the parallel light rays from behind a screen, we will direct them from the front, they will shine in the same direction as before. Reflected by the reflective circular silver areas on a screen, they will interfere with each, recreating a bright spot exactly at point S, where the original point light used to be.
That's how our second task, recreating an image of a point light, can be accomplished.


No comments:
Post a Comment