Minkowski Space+Time
Imagine a point moving in a circle on a two-dimensional
As it moves, we can register its position on this plane and obtain its trajectory.
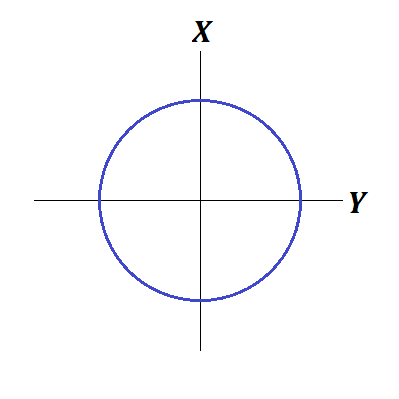
Does this trajectory fully represent graphically the motion of a point?
The answer is NO, because this trajectory does not reflect the time when our point visited this or that location on a circle.
The point might uniformly rotate along this circle, it might stop every once in awhile or even start rotating in the opposite direction. Trajectory will be the same - a circle.
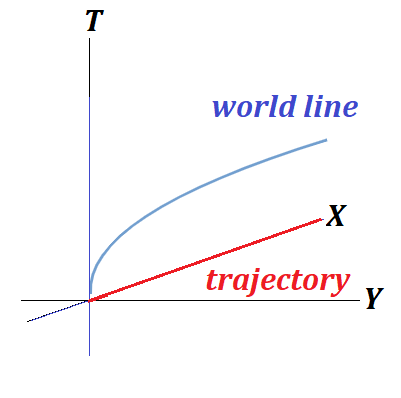
To better represent the motion, let's add a third dimension - the time axis T.
Now, if the point occurs at coordinates (x,y) on a plane at time t, we will represent it as a point with coordinates (x,y,t) in our three-dimensional
This point with added time coordinate is called the world point.
Assume, a point uniformly rotates along a circle with a constant angular speed. Then its three-dimensional
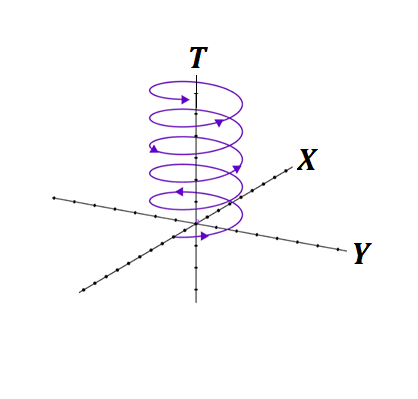
The above picture graphically fully represents the motion - uniform rotation of a point in a circle on a plane.
The line our world point is moving along is called the world line that fully represents the motion.
Granted, we live in a three-dimensional world and our movements are in three-dimensional
So, to fully represent the motion, we have to add the fourth dimension - time.
The problem is, it's practically impossible to graphically present a four-dimensional space on a paper or a screen, or a whiteboard.
So, to preserve the clarity of the graphical representation of a motion, we will continue to use examples of motion on a plane, adding the time as the third dimension.
It should be assumed, however, that when we use
Examples of World Lines
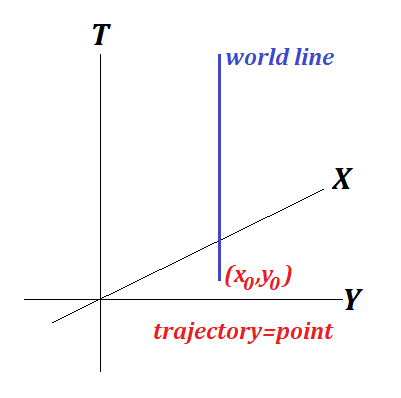
1. Being at rest at a fixed point on XY-plane
Being at rest can be described by equations
x(t) = x0
y(t) = y0
where
x0 is the
y0 is the
Therefore, as time t increases, the world line, starting at the initial point on XY-plane, goes vertically retaining X- and Y-coordinates.
The projection of this world line onto XY-plane is a point with XY-coordinates (x0,y0).
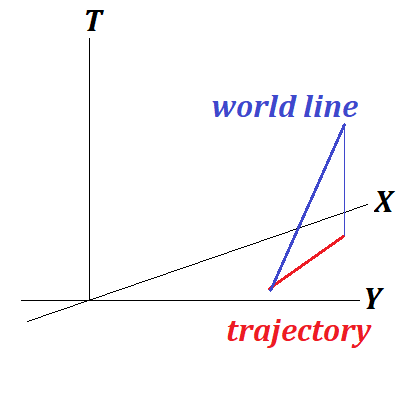
2. Uniform movement along a straight line on an XY-plane
Since a point is uniformly moving on a plane along a straight line, it's X- and
x(t) = x0 + a·t
y(t) = y0 + b·t
where
x0=x(0) is the starting
y0=y(0) is the starting
a and b are real constants.
Therefore, if (x,y,t) is any world point that represent a position of a point on a plane (x,y) at time t, the following equations must be true:
x = x0 + a·t
y = y0 + b·t
t = t0 + c·t (where t0=0, c=1)
which is a classical representation of a straight line in 3D passing through a point
The projection of this world line onto XY-plane is a trajectory of a point on a plane - a straight line expressed by an equation
(x−x0)/a = (y−y0)/b
3. Straight line movement with constant acceleration on an
Let's assume for simplicity that a point on an
Then, according to familiar rules of Newtonian mechanics, we can write
x(t) = a·t²/2
y(t) = 0
The world line of this motion lies in the plane y=0 and is a parabola.
Distance in Space-Time
For better illustration, instead of considering our three-dimensional space and one-dimensional time, we continue restricting our analysis to two-dimensional space + one-dimensional time coordinates to be able to graphically represent the resulting three-dimensional space+time continuum.
In addition, to use the same units of measurement (length units, like meters) along all three
Since speed of light in vacuum c is a universal constant in all inertial reference frames, this does not change the character of the curves we construct.
One of the most important characteristic of any space is the method of calculating the distance between two points.
Since we talk about real physical space+time continuum, the definition of a distance between two points A and B should give the same result if measured in any inertial system of coordinates introduced in our space+time.
In other words, the distance between two points in space+time must be an invariant relative to coordinate transformation from one inertial system to another.
In the previous parts of this course, Galilean View and Einstein View, we have determined that the Principle of Relativity and constancy of the speed of light in vacuum in any inertial frame of reference dictate a new approach to transformation of coordinates from one inertial reference frame to another.
In particular, the proper transformation of coordinates is so-called Lorentz transformation that takes into account time dilation and changes in length of moving objects.
The old Euclidean definition of a distance d(A,B) between two points A and B is not an invariant relative to Lorentz transformation (see the lectures Non-Invariance in the Galilean View part and Lorentz Transformation in the Einstein View part of this course).
At the same time, in the lecture Relativity Metric of Einstein View part of this course we have introduce a new expression that is invariant relative to Lorentz transformation:
d²(A,B) = (XB−XA)² + (YB−YA)² + (ZB−ZA)² − c²·(TB−TA)²
In 1907 Hermann Minkowski, German physicist and mathematician, proposed to represent the world we live in as a four-dimensional space+time continuum (three space coordinates + one-dimensional time) and use the expression above as a definition of a distance between two world points in this Minkowski space+time.
Thus defined, the distance between two world points is an invariant relative to Lorentz transformation.
Note that many other definitions of invariant metric in Minkowski space+time can be derived by applying any function to an expression for d²(A,B) above.
For example, to have the value of the Minkowski distance between two points along a world line as a positive value (see the next lecture Past and Future), many physicists use the negative of this expression as a measure of a distance between two world points
D²(A,B) = c²·(TB−TA)² − (XB−XA)² − (YB−YA)² − (ZB−ZA)²


No comments:
Post a Comment