Relativistic Momentum
One of the fundamental laws of Newtonian mechanics is the Second Law describing the relationship between a vector of force F, inertial mass m and a vector of acceleration a
F = m·a
where inertial mass m is considered a constant characteristic of an object independent of time, space or motion.
Since a vector of acceleration a, by definition, is the first derivative of a vector of speed v by time t, the same law can be written as
F = m·dv/dt = d(m·v)/dt
The product of mass and a vector of speed is a vector of momentum of motion p=m·v, so the same Second Law can be written as
F = dp/dt
The Conservation Law of Momentum, based on uniformity of space, states that the conservation of momentum is universal and should be maintained through transformation from one inertial frame to another (see the previous lecture Noether Theorem in this course).
That's why it makes sense to consider the latter expression of the Newton's Second Law in terms of a derivative of the momentum of motion as the most appropriate form.
It makes sense to discuss the physical meaning of a momentum and its expression as a product of mass and velocity.
As seen from the last formula, a force is a rate of change of a momentum. The greater the change of momentum - the greater force that caused its change.
From another perspective, the momentum can be viewed as a degree of resistance to the change of motion.
Consider an object uniformly moving along a straight line and some external force that tries to change this motion.
It is intuitively acceptable that an object with greater mass resists the changes to its movement stronger and, therefore, requires stronger force to achieve similar change in motion.
Similarly, the faster an object moves - the more difficult to change its trajectory, and we can reasonably assume that an object with higher speed of movement requires stronger force to changes its movement.
The purpose of this lecture is to analyze the transformation of momentum from one inertial frame to another using the Law of Conservation of Momentum as a tool.
We do know how relativistic speed is transformed (see lectures Einstein View - Adding X-Velocitis and Einstein View - Adding Y-,Z-Velocitis in this course).
The Law of Conservation of Momentum will help us to determine how an object's momentum changes when viewed from different reference frames.
Let's analyze the ideal elastic collision of two identical spherical objects as shown on the following pictures describing this collision in the reference frame β{x,y,z,t} at rest relative to the point of collision (the origin of coordinates) and positioned symmetrically to the objects.
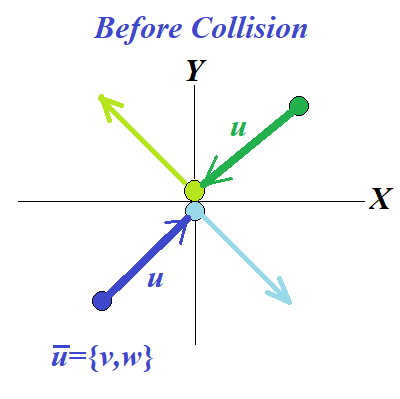
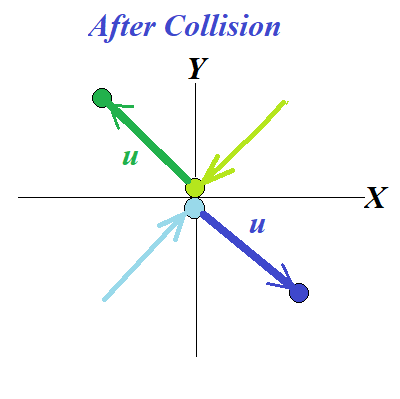
Assume, the spherical blue and green objects are uniformly moving on parallel trajectories in opposite directions with the same by magnitude velocity
This assures the mirror-like trajectories before and after the collision.
Summary of x,y-components (v,w) of velocity vectors u for both objects before and after the collision can be presented in the following table
| Object | Before (x,y) | After (x,y) |
| Green | (−v,−w) | (−v,w) |
| Blue | (v,w) | (v,−w) |
Since in the β-frame both objects have the same mass and speed magnitude and move in the opposite directions before and after the collision, the total momentum of both should be zero before and after the collision. The Law of Conservation of Momentum is held.
Obviously, the Law of Conservation of Momentum as a vector must be held separately for its X- and Y-components.
Let's now switch to another reference frame and apply the Law of Conservation of total Momentum of both objects.
Consider an inertial reference frame α{X,Y,Z,T}.
Assume that β-frame {x,y,z,t} is uniformly moving along the X-axis of this α-frame with some constant speed s maintaining parallelism and directionality of all axes, and at some initial time both frames coincide.
Recall the laws of relativistic addition of velocities presented earlier in the lecture Adding Y-, Z-Velocities within Einstein View part of this course
| uαx = |
|
| uαy = |
|
Let's calculate the X- and Y-components of both green and blue objects in α-frame before and after the collision.
1. The horizontal x-component of the green object's velocity in β-frame is, as we stated above, uβx=−v before and after the collision.
Therefore, in α-frame before and after the collision its X-component is
| uαx = |
|
2. The value of vertical y-component of velocity of a green object in β-frame is, as we stated above, −w before the collision and w after the collision.
Therefore, before the collision in α-frame, substituting uβy=−w and uβx=−v, the vertical component of the green object is
| uαy = |
|
3. After the collision in α-frame, substituting uβy=w and uβx=−v, the vertical component of the green object is
| uαy = |
|
4. Let's examine the blue object now.
In the original β-frame its horizontal speed along x-axis is v before and after the collision, while its vertical speed along y-axis is w before and −w after the collision.
Using the same formulas of adding velocities, the horizontal speed of the blue object in α-frame before and after the collision is
| uαx = |
|
5. The value of vertical component of velocity of a blue object in β-frame is, as we stated above, w before the collision and −w after the collision.
Therefore, before the collision in α-frame, substituting uβy=w, the vertical component of the blue object is
| uαy = |
|
6. After the collision in α-frame, substituting uβy=−w the vertical component of the blue object is
| uαy = |
|
Summary of velocities in α-frame:
| Object | Speed | Value | ||
| Green | X before |
|
||
| Blue | X before |
|
||
| Green | X after |
|
||
| Blue | X after |
|
||
| Green | Y before |
|
||
| Blue | Y before |
|
||
| Green | Y after |
|
||
| Blue | Y after |
|
Not surprisingly, the lengths² of velocity vectors, being the same in the β-frame for both objects
Green object's velocity vector length² in α-frame (lα²) is
[(s−v)²+w²(1-s²/c²)] /(1−s·v/c²)²
Blue object's velocity vector length² in α-frame (lα²) is
[(s+v)²+w²(1-s²/c²)] /(1+s·v/c²)²
Newtonian momentum of an object of mass m moving in two-dimensional Euclidean inertial reference frame with some velocity vector u={v,w} is a vector m·u={m·v,m·w}.
The rules of addition of velocities when observing the movement from another inertial reference frame are simple vector addition derived from Galilean transformation of coordinates.
Since X-component of each object's velocity before and after a collision in α-frame are the same, the X-component of the total momentum of both objects, calculated according to classical Newtonian definition as a product of an object's mass by its velocity vector, would obviously be the same before and after the collision.
The situation is completely different along Y-axis.
If we try to check the law of conservation of momentum calculated according to classical Newtonian definition as mass times speed along each axis, we obtain the following results.
Before a collision the total Newtonian momentum of both green and blue objects along Y-axis is
|
+ |
|
After a collision the total Newtonian momentum of both green and blue objects along Y-axis is
|
+ |
|
The only cases when they are equal is if s·v=0 or w=0, that is either s=0, which means β-frame is not moving relative to α-frame or v=0, that is no horizontal movement, or w=0, that is no vertical movement.
Classical Newtonian definition of a momentum is not working in relativistic mechanics in general cases..
To address this problem, the relativistic momentum is defined differently than the classical Newtonian one.
Relativistic momentum of an object is its Newtonian-like momentum (product of mass and velocity vector) multiplied by factor γ=1/√1 − l²/c², where l is the magnitude (length) of a velocity vector.
Modified this way, the relativistic momentum is preserved in the collision we use as an example.
The step-by-step proof of the Law of Conservation of Relativistic Momentum can be viewed on page Proof of Conservation of Relativistic Momentum (there are a lot of formulas there, so open it in a new tab for clarity by right-click and choosing to open in a new tab).
Let's summarize our results.
Assume, in our reference frame two objects of mass m each are moving towards each other on a collision course. Their velocities have the same magnitude u and we assume ideal elastic collision between them.
We have proven the law of conservation of their total relativistic momentum in the course of their collision, where the relativistic momentum of each is calculated according to this formula
| p = γ·m·|u| = |
|
The interpretation of the denominator in the expression for relativistic momentum is a matter of opinion.
Some physicists prefer considering the mass of an object as changing with the speed and call the expression
γ·m = m/√1−|u|²/c²
a relativistic mass.
Some others prefer to relate the factor γ as applicable to an entire relativistic momentum, leaving mass unchanged and calling it a rest mass, emphasizing this by using a subscripted version m0
| p = γ·m0·|u| = |
|


No comments:
Post a Comment