Doppler Effect for Sound Waves
In this lecture we will consider longitudinal sound waves in the air and dependence of their frequency at the source of sound with a perceived frequency by an observer moving relatively to this source with a speed less than the speed of sound waves propagation.
Obviously, the analysis is applicable to other types of waves and media where these waves propagate.
We will consider the situation when the source of sound is at some fixed position and an observer is moving to or from this source with certain speed v.
The case when observer is at rest and the source of sound moves to or from an observer is no different than the above.
The case when both the source of sound and an observer are moving is just a combination of the above, as only the relative speed of an observer relative to a source of sound is really important.
For simplicity, we will consider only a one-dimensional case when both a source of a sound and an observer are always on the X-axis of some Cartesian coordinate system.
More complicated case of three-dimensional movement involves more calculations but is not important from the conceptual viewpoint.
Let's assume that a source of sound is at position x=0 and the speed of sound waves propagation in the air is u.
Let's assume further that the frequency of oscillations produced by a source of sound is f0 and waves propagate along X-axis in both direction with the same speed u mentioned above.
Then the standard relationships among parameters of oscillation are:
period T0 = 1/f0
wavelength λ0 = u·T0 = u/f0
frequency f0 = u/λ0
Case 1 - Observer moves towards a source of sound with speed v.
Let's take some relatively long time interval t substantially greater than a period of oscillations T0.
If an observer stands still (v=0) during this time interval t, considering the period of oscillations is T0, the number of waves passing the observer would be N0=t/T0.
If during time t there are N0 waves passing an observer, the perceived frequency of sound would be
N0 /t = (t/T0)/t = 1/T0 = f0
which is the original frequency of sound produced by a source.
So, a standing still observer perceives the same sound frequency as was emitted by a source of sound.
Assume now that an observer at an initial distance a (greater than zero) is moving with speed v (less than the speed of sound u) towards the source of sound.
Again, let's choose some time interval t, not very small (substantially larger than period of oscillations T0) but not too long, so an observer will not reach the source of sound (that is, t should be less that a/v).
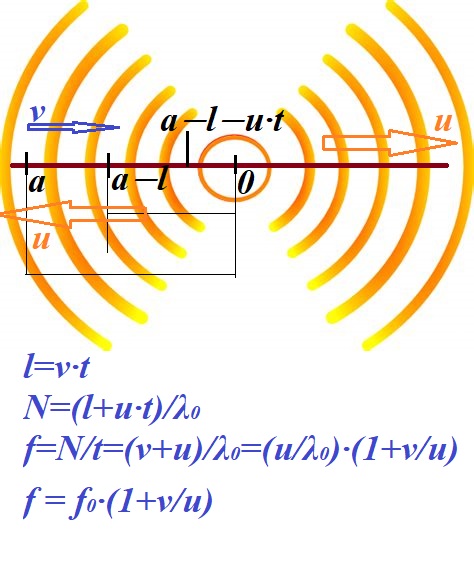
If an observer is moving towards a source of sound with speed v during time t, he will cover the distance l=v·t and will come to a point at distance a−l from the source of sound.
Let's calculate how many waves of sound will pass an observer during this time interval.
In other words, how many waves will fall into a zone of perception of an observer.
The first wave to cross will be where an observer started, that is at distance a from the source.
Obviously, all waves that are already in the interval from distance a−l to distance a will be crossed.
In addition, all those sound waves, moving with speed u and positioned at the beginning of time closer to a source of sound at a distance from a−l−u·t to a−l by the time t will come to a distance of a−l or larger from the origin of sound, thereby crossing an interval where an observer can hear them.
Therefore, all waves that at time t=0 are at a distance from a source of sound from a−l−u·t to a will cross ways with an observer during time t.
The number of these waves is
N = (l+u·t)/λ0
If an observer hears N sound waves during time t, the perceived frequency of sound is
f = N/t = (u·t+l)/(λ0·t) =
= (u+v)/λ0 = (u/λ0)·(1+v/u) =
= f0·(1+v/u)
As we see, the perceived frequency f by an observer moving towards a fixed in the medium source of sound is greater than the frequency emitted by this source f0 by a factor 1+v/u, where u is the speed of sound emitted by a source and v is the speed of an observer.
Case 2 - Observer moves away from a source of sound with speed v.
Now the zone of an observer's perception is from a distance a from a source of sound to distance a+l, where l=v·t.
Initially, in this zone of perception there were l/λ0 waves of sound. But, as the time goes and an observer gets closer to the end of his zone of perception at distance a+l, all these waves will escape this zone because they move quicker than an observer.
Instead, some waves that are behind an observer (closer to a source of sound) will be able to be in the zone of perception and be heard by an observer because they will overcome him by moving faster.
The first wave an observer perceives is the one at his initial position at distance a from a source of sound.
The last wave he perceives is the one that by time t is at the end of his perception zone at distance a+l from the source, that is that at time t=0 was at distance a+l−u·t from a source.
Therefore, all waves that at time t=0 are at the distance from a+l−u·t to a will be perceived by an observer moving from distance a to distance a+l from a source.
The interval from a+l−u·t to a is u·t−l long.
It contains all the waves heard by an observer while he moves from distance a to a+l.
The number of these waves is
N = (u·t−l)/λ0
The perceived frequency of sound is
f = N/t = (u·t−l)/(λ0·t) =
= (u−v)/λ0 = (u/λ0)·(1−v/u) =
= f0·(1−v/u)
As we see, the perceived frequency f by an observer moving away from a fixed in the medium source of sound is smaller than the frequency emitted by this source f0 by a factor 1−v/u, where u is the speed of sound emitted by a source and v is the speed of an observer.
Incidentally, this formula shows why we consider only a case of a speed of an observer to be smaller than a speed of sound. If that condition is not met, we would have a negative frequency, so formula would not be correct.


No comments:
Post a Comment