Geometry+ 09 : UNIZOR.COM - Math+ & Problems - Geometry

Notes to a video lecture on http://www.unizor.com

Geometry+ 09

Theorem A

Given two parallel lines, point M not on any of them and not in-between them, and two lines from this point M intersecting the given parallel lines at points A, B (on a far line), C and D (on a near line).
So, ACDB is a trapezoid.
Opposite intersection points are connected by segments AD and BC intersecting themselves at point Q.
Line connecting points M and Q intersects CD at point P and is extended to intersect AB and point N.

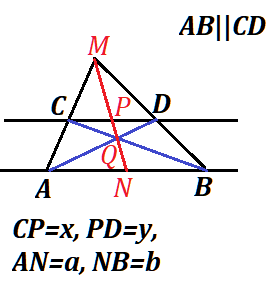
Prove that point P is a midpoint of CD and point N is a midpoint of AB.

Proof A
Let's use the symbols:
CP=x, PD=y, AN=a, MB=b.
Consider triangles
ΔAMN and ΔCMP.
They are similar because all angles are correspondingly equal.
Therefore,
x/a = MP/MN
Consider triangles
ΔBMN and ΔDMP.
They are similar because all angles are correspondingly equal.
Therefore,
y/b = MP/MN = x/a
Consider triangles
ΔCPQ and ΔBNQ.
They are similar because all angles are correspondingly equal.
Therefore,
x/b = PQ/QN
Consider triangles
ΔDPQ and ΔANQ.
They are similar because all angles are correspondingly equal.
Therefore,
y/a = PQ/QN = x/b
Now we have
y/b = x/a and
y/a = x/b
Simple algebraic transformations lead us to the following:
y·a = x·b and
y·b = x·a
All variables are positive real numbers, so we can divide the first equation by the second, canceling x and y, getting
a/b = b/a
a² = b²
a = b
From this follows
x = y
End of Proof.


Problem B

Given two parallel lines and a segment AB on one of them.
Using only a straight line ruler, divide segment AB in two equal parts.

Solution B
The solution is based on the results of Problem A above.
All we need to do is to pick up any point M, like the one on a picture above, connect it to points A and B with points C and D being the intersections of MA and MB with another parallel line.
The figure ABCD is a trapezoid, its diagonals AD and BC intersect at point Q. Line MQ with an extension to pointN bisects segments AB and CD at point N.


Problem C

Given two parallel lines and a segment AB on one of them.
Using only a straight line ruler, double the length of this segment.
In other words, find point B' on the same line where AB is located such that the length of AB equals to the length of BB'.

Solution C
First of all, pick any segment CD on another parallel line (not the one where AB is on) and divide it in half by point P, as explained in the Problem B.
Draw one line through points A and C and another through points B and P.
Assuming these line are not parallel, let M be their point of intersection (if AC||BP, choose different point D and start again.)
Line MD will cross line where segment AB is located at point B'. Segments AB and BB' will have equal lengths because CP and PD are of equal length (the proof is trivial, it follows from similarity of triangles.)