Notes to a video lecture on http://www.unizor.com
Definition of Mechanical Power
To analyze the motion, we often use a concept of speed.
Let's assume that an object moves in some inertial reference frame, and
the distance covered by it from its initial position along its
trajectory is a function of time S(t).
Recall the definition of speed of an object as the rate, at which this object covers the distance along its motion along a trajectory.
In case of a uniform motion we can simply divide the distance S, covered during time t, by the time t to get the speed:
V = S/t
In case of non-uniform motion the speed changes and at any particular moment of time t an instantaneous speed can be calculated using differentials:
V(t) = dS(t)/dt
To analyze the mechanical work performed to achieve certain results, we often use a concept of power.
Let's assume that something or someone performs certain work and, as the time goes by, the work performed is a function of time W(t).
The power is the rate, at which the work is performed.
If during the time t the work performed is W, we define the average power of the whoever or whatever performs the work as
P = W/t
Most likely, at equal in length but different time intervals the amount
of work performed will be different. For example, when a car starts, its
engine should give a car an acceleration, which requires more work per
unit of time than to maintain a constant speed on a smooth straight
road.
In cases like this we can talk about an instantaneous power as a function of time that can be calculated using differentials:
P(t) = dW(t)/dt
Consider an example of an object in uniform motion against the force of friction with a constant speed V.
The force F that moves it forward must be equal in
magnitude and opposite in direction to the force of friction to maintain
the constant speed. Since the friction is constant, the force F must be constant as well.
The distance S covered as a function of time t is
S(t) = V·t
Therefore, the work performed by the force F during the time t is
W(t) = F·S(t) = F·V·t
From the definition of power follows that the power this force F exhorts is
P(t) = dW(t)/dt = F·V
As an example, the car engine exhorts the same power and consumes the
same amount of gas per unit of time, if the car uniformly moves along a
straight road. This power is used to generate a force sufficient to
overcome the friction of wheels and air resistance.
Consider a more general case, when the motion is not uniform.
Assume, an object of mass m moves as a result of action of force F(t), where t is time. The distance it covers is S(t).
Then during an infinitesimal time interval from t to t+dt the work performed by this force will be
dW(t) = F(t)·dS(t)
Considering the Newton's second law,
F(t) = m·a(t),
where a(t) is acceleration.
Increment of distance is
dS(t) = V(t)·dt,
where V(t) is an object's speed.
Also, by definition of acceleration,
a(t) = dV(t)/dt
Therefore,
dW(t) = (m·dV(t)/dt)·V(t)·dt =
= m·V·dV(t)
Power exhausted by this force is, therefore
P(t) = dW(t)/dt =
= m·V·dV(t)/dt =
= m·V(t)·a(t)
From the definition of power as amount of work per unit of time or, more precisely, the first derivative of work by time
P(t) = dW(t)/dt
follows that the unit of measurement of power is joule/sec called watt.
Expanding the definition of joule as newton·meter,
1 watt = 1J/sec = 1N·m/sec
Obvious extensions of unit of power watt are
kilowatt = 1,000 watt and
megawatt = 1,000,000 watt.
There is an old unit of power called horsepower.
Metric horsepower, derived from lifting up against a force of gravity on Earth a weight of mass 75 kg with a constant speed of 1 m/sec, is related to watt unit as
1(metric HP) =
=75(kg)·9.8(m/sec²)·1(m/sec)≅
≅ 735.5(W)
For historical reasons there is also a mechanical horsepower, defined as 33,000 pound-feet per minute, related to watt unit as
1(mechanical HP) ≅ 745.7(W)
So, a car engine of 200 mechanic horsepower has the power of about 149,140 watt.
Watt, as a unit of measurement, was called in honor of James
Watt, an 18th century Scottish scientist who was one of the first to
research a concept of power, developed steam engines and measured the
power of a horse.
Now let's address the concept of power in a case of rotation with constant angular speed. An example is lifting a bucket of water from a well.
Assume, a bucket of water has a mass m and we lift it with constant linear speed V with an angular speed of the well's wheel ω=V/R, where R - radius of a well's wheel.
Since the speed is constant, the force F that acts on a bucket equals to m·g, where g - acceleration of the free fall.
At the same time, if the wheel is turned by some motor and R is the radius of its shaft, the motor manufacturer provides technical characteristic not only of the power, but also of a torque of a motor.
Remember that the torque equals to
τ = F·R
So, on one hand, we have expressed the power of a motor P in terms of unknown force F and linear speed of a bucket:
P = F·V = F·R·ω
On another hand, we expressed the torque of this motor in terms of the same unknown force F and a radius of its shaft:
τ = F·R
Substituting torque τ for F·R in the formula for power, we can find the relationship between the power of a motor and is torque:
P = τ·ω
Notice the similarity between the formula for power in case of uniform motion along a straight line P=F·V and formula for power in case of rotation with constant angular speed P=τ·ω. Instead of force F in case of straight line motion, we use torque τ for rotation and, instead of linear speed V for straight line motion, we use angular speed ω for rotation.
Let's check this with real data about a particular engine.
Below is a graph representing the power and torque of Ford Motor Company 6.7L Power Stroke diesel V-8.
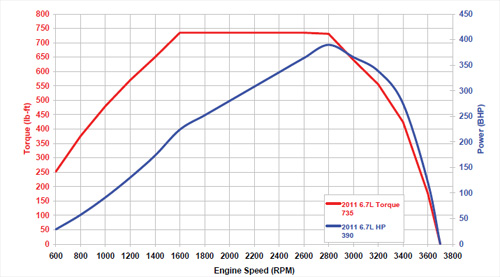
As you see, the power and torque grow relatively monotonically until
some engine limitations start playing significant role. While in the
area of monotonic growth, we can take a particular angular speed, say,
1400 RPM (revolutions per minute) and see that the power of an engine
equals approximately 174 HP (mechanical horsepower) and the torque is
about 650 Lb-Ft (pound-feet).
Let's check if the relationship between power and torque derived above is held in this case.
First of all, we transform all units into standard physical measures defined in SI:
1 RPM (revolutions per minutes) =
= 2π radian per minute =
= 2π/60 radians/sec =
= 0.1048 rad/sec
1 HP = 745.7 W = 745.7 J/sec
1 Lb-Ft = 1.35582 J
Substituting all the above, we see that
angular speed is equal to
1400·0.1048 = 146.6 rad/sec
power is
174·745.7 = 129,751.8 J/sec
torque equals to
650·1.35582 = 881.3 J
Now we can check the relationship between the power, torque and angular speed
P = τ·ω
Indeed,
881.3·146.6 = 129,198.6
As we see, the difference between power and a product of torque by
angular speed is minimal, attributable to imprecise measurement of the
parameters and graph reading.


No comments:
Post a Comment